
- •2. Сравнение числовых рядов
- •12. Понятие ортогональной системы действительной функций. Ортогональность основной тригонометрической системы
- •13. Ортогональные системы действительных функций (определение, примеры). Разложение функции по ортогональным системам
- •14. Ряд Фурье. Представление периодической функции в виде ряда Фурье. Сходимость ряда Фурье (теорема Дирихле)
- •15. Разложение в ряд Фурье четных и не четных функций периодических функций. Разложение функций в ряд Фурье, заданной на полупериоде.
- •19. Интеграл Фурье в комплексной форме.
- •20. Теорема о существовании преобразования Фурье
- •21. Синус и косинус преобразования Фурье
- •26. Уравнение Бернулли. Его решение
- •27. Решение линейного диф-го уравнения 1го порядка методом Лагранжа
- •28. Уравнение в полных дифферен. И его решение
- •30. Линейные однородные ур-я 2-го порядка с постоянными коэ-ми. Их решение
- •31. Линейные неоднородные ур-я 2-го порядка с постоянными коэф-ми и правой частью спец. Вида
- •32. Линейные однород. Ур-ния n-го порядка
- •33. Решение линейных дифферен. Ур-ний n-го порядка с постоян коэф.
- •43. Непрерывность функции нескольких переменных
- •44. Частное приращение и частная производная функции нескольких переменных
- •45. Полное приращение функции нескольких переменных
- •47. Касательная плоскость
- •48. Частные производные высших порядков
- •51. Понятие двойного интеграла
- •52.Свойства двойного интеграла
- •53 Теоремы об оценке 2го интеграла
- •54 Техника вычисления 2го интеграла
- •55.Замена переменных в 2ом интеграле
45. Полное приращение функции нескольких переменных
Полное приращение функции двух переменных — приращение функции, которое соответствует приращению обоих аргументов:

Полное приращение не равно сумме частных приращений.
Полное
приращение функции
переменных


Полный дифференциал функции нескольких переменных
Полный дифференциал функции двух переменных — главная часть полного приращения функции, равная сумме произведения частной производной функции по первой переменной на приращение первого аргумента и произведения частной производной функции по второй переменной на приращение второго аргумента:
 или
или

Полный дифференциал функции переменных:


46.Сложная
функция двух переменных — промежуточные
переменные которой так же являются
функциями двух переменных:

Сложная
функция
переменных — функция, аргументы которой
являются также функциями нескольких
переменных:
 .
.
Теорема о частной производной сложной функции
Если
функция
 и промежуточные переменные
и промежуточные переменные
 дифференцируемы, то частные производные
сложной функции
вычисляются по формулам:
дифференцируемы, то частные производные
сложной функции
вычисляются по формулам:


Для функции переменных теорема формулируется аналогично:
 ,
,
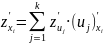 В
общем случае,
В
общем случае,

Полный дифференциал сложной функции
Рассмотрим
сложную функцию
 .Учитывая,
что
.Учитывая,
что
 и
и
 , получаем:
, получаем:
 .
Раскрывая скобки и группируя получим:
.
Раскрывая скобки и группируя получим:
 Где
выделенные части, соответственно
Где
выделенные части, соответственно
 и
и
 .
.
Следовательно,

Частные производные неявно заданной функции многих переменных
Если функция задана неявным образом уравнением , то частные производные функции вычисляются по формулам:

Для
функции
переменных аналогично:

47. Касательная плоскость
Касательная плоскость к поверхности в некоторой точке — плоскость, проходящая через данную точку и содержащая все касательные прямые к поверхности в этой точке.
Уравнение
касательной плоскости к поверхности в
точке
 ,
, имеет вид:
имеет вид:
Если поверхность задана явным образом функцией ,
то

Если поверхность задана неявным образом

то

(в учебнике в последней сумме тоже нет)
Нормаль к поверхности
Нормаль (нормальная прямая) к поверхности в некоторой точке — прямая, проходящая через данную точку перпендикулярно касательной плоскости.
Уравнение
нормали к поверхности в точке
 имеет вид:
имеет вид:
Если поверхность задана явным образом функцией , то

Если поверхность задана неявным образом то

Геометрический смысл полного дифференциала
Геометрически
смысл полного дифференциала функции
двух переменных. Рассмотрим функцию
которая в точке
имеет дифференциал
 Уравнение касательной плоскости
Уравнение касательной плоскости
 к поверхности, заданной функцией в точке
к поверхности, заданной функцией в точке

 (
( .
Учитывая, что
.
Учитывая, что
 видим, что правые части этих равенств
совпадают, следовательно:
видим, что правые части этих равенств
совпадают, следовательно:
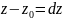 .
Таким образом, полный дифференциал
функции равен приращению аппликаты
касательной плоскости при переходе от
точки
к точке
.
Таким образом, полный дифференциал
функции равен приращению аппликаты
касательной плоскости при переходе от
точки
к точке
 ).
).
48. Частные производные высших порядков
Частная
производная -го порядка — частная
производная от частной производной
 -го
порядка.
-го
порядка.
Частный случай:
Частных производных второго порядка от функции двух переменных может быть четыре:
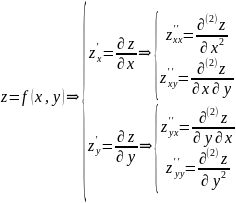
Смешанная частная производная — частная производная второго или более высокого порядка, взятая по разным переменным.
Полные дифференциалы высших порядков
Полный дифференциал второго порядка — дифференциал от дифференциала функции.
Для функции полный дифференциал второго порядка:

Полный дифференциал порядка — дифференциал от дифференциала -го порядка.
49.
50.
