
- •2. Сравнение числовых рядов
- •12. Понятие ортогональной системы действительной функций. Ортогональность основной тригонометрической системы
- •13. Ортогональные системы действительных функций (определение, примеры). Разложение функции по ортогональным системам
- •14. Ряд Фурье. Представление периодической функции в виде ряда Фурье. Сходимость ряда Фурье (теорема Дирихле)
- •15. Разложение в ряд Фурье четных и не четных функций периодических функций. Разложение функций в ряд Фурье, заданной на полупериоде.
- •19. Интеграл Фурье в комплексной форме.
- •20. Теорема о существовании преобразования Фурье
- •21. Синус и косинус преобразования Фурье
- •26. Уравнение Бернулли. Его решение
- •27. Решение линейного диф-го уравнения 1го порядка методом Лагранжа
- •28. Уравнение в полных дифферен. И его решение
- •30. Линейные однородные ур-я 2-го порядка с постоянными коэ-ми. Их решение
- •31. Линейные неоднородные ур-я 2-го порядка с постоянными коэф-ми и правой частью спец. Вида
- •32. Линейные однород. Ур-ния n-го порядка
- •33. Решение линейных дифферен. Ур-ний n-го порядка с постоян коэф.
- •43. Непрерывность функции нескольких переменных
- •44. Частное приращение и частная производная функции нескольких переменных
- •45. Полное приращение функции нескольких переменных
- •47. Касательная плоскость
- •48. Частные производные высших порядков
- •51. Понятие двойного интеграла
- •52.Свойства двойного интеграла
- •53 Теоремы об оценке 2го интеграла
- •54 Техника вычисления 2го интеграла
- •55.Замена переменных в 2ом интеграле
43. Непрерывность функции нескольких переменных
Функция
нескольких переменных
 непрерывна
в некоторой точке
из своей области определения, если при
стремящемся к данной точке значении
аргумента стремится к нулю приращение
значения функции:
непрерывна
в некоторой точке
из своей области определения, если при
стремящемся к данной точке значении
аргумента стремится к нулю приращение
значения функции:

Данное определение означает, что функция непрерывна в точке, если предел функции существует в этой точке и равен значению функции в этой точке.
Свойства непрерывных функций многих переменных
Непрерывность суммы функций: сумма конечного числа непрерывных функций является непрерывной функцией.
Непрерывность разности функций: разность двух непрерывных функций является непрерывной функцией.
Непрерывность произведения функций: произведение конечного числа непрерывных функций является непрерывной функцией.
Непрерывность частного функций: частное двух непрерывных функций (при условии, что знаменатель не равен нулю) является непрерывной функцией.
Теорема о наибольшем и наименьшем значении: непрерывная в закрытой области функция достигает в некоторых точках данной области своих наибольшего и наименьшего значений.
Теорема о промежуточных значениях: непрерывная в закрытой области функция принимает все промежуточные значения между ее наибольшим и наименьшим значениями.
Теорема о прохождении через ноль: если непрерывная в закрытой области функция принимает на границе данной области значения разных знаков, то в данной области имеется точка или линия, в которой данная функция равна нулю.
44. Частное приращение и частная производная функции нескольких переменных
Частное приращение функции двух переменных —приращение функции, которое соответствует приращению одного из аргументов. А именно:
частное
приращение по аргументу

частное
приращение по аргументу

Частное
приращение функции
переменных
 :
:

Частная производная функции двух переменных по некоторому аргументу — предел отношения частного приращения функции по данному аргументу к приращению этого аргумента, при стремлении его к нулю. А именно, частная производная функции
по
аргументу

по
аргументу

Частная производная функции нескольких переменных:

Обозначения
частной производной функции:

Частное приращение и дифференциал функции нескольких переменных
Есть
функция
 непрерывная в области
непрерывная в области
 .
.
 — внутренняя точка области
,
тогда
— внутренняя точка области
,
тогда

Из теоремы о связи бесконечно малой величины с пределом следует, что

Величина
 называется главной частью частного
приращения
называется главной частью частного
приращения
 функции
в точке
функции
в точке
 .
.
Частный дифференциал функции двух переменных по некоторому аргументу — главная часть приращения функции, равная произведению частной производной функции на приращение соответствующего аргумента. А именно:
частный
дифференциал функции по аргументу

частный
дифференциал функции по аргументу

Частный дифференциал функции переменных по некоторому аргументу:

Геометрический и физический смысл частной производной функции двух переменных
Геометрический смысл частной производной функции двух переменных:
Функция
задает в пространстве поверхность.
 — точка из области определения функции.
Плоскость
— точка из области определения функции.
Плоскость
 параллельна плоскости
параллельна плоскости
 и пересекает поверхность по линии
и пересекает поверхность по линии
 Частная производная функции двух
переменных
Частная производная функции двух
переменных
 совпадает с производной функции одной
переменной
совпадает с производной функции одной
переменной
 по
— это тангенс угла наклона касательной,
параллельной
по
— это тангенс угла наклона касательной,
параллельной
 в точке
:
в точке
:

Аналогично,
плоскость
 пересекает поверхность по линии
пересекает поверхность по линии
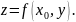 Угол наклона касательной, параллельной
Угол наклона касательной, параллельной
 в точке
равен
в точке
равен
 и верны равенства:
и верны равенства:

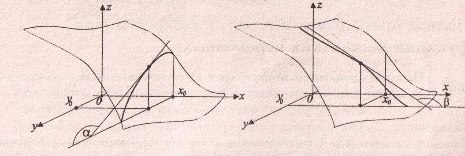 (формулы
местами не перепутал, в книге так)
(формулы
местами не перепутал, в книге так)
Физический
смысл частной производной двух переменных:
мгновенная скорость изменения функции
при перемещении точки
 параллельно одной координатной оси.
параллельно одной координатной оси.
Геометрический смысл частного дифференциала функции двух переменных: частный дифференциал функции по некоторой переменной равен приращению аппликаты касательной при изменении данной переменной.
