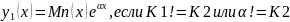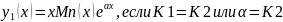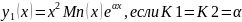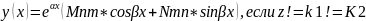30. Линейные однородные ур-я 2-го порядка с постоянными коэ-ми. Их решение

ay’’+by’+cy=0 a,b,c-константы

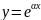
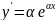
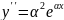
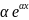a +b +c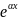 =0 делим на

a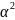 +b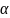 +c=0 -характеристическое уравнение

если корни различные:

y(x)=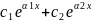

если корни мнимые:

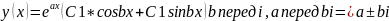
если корни совпадают:

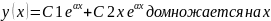
31. Линейные неоднородные ур-я 2-го порядка с постоянными коэф-ми и правой частью спец. Вида

)

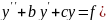сначала решаем однородное, потом по теоремам частное:

T1:Если у₁-частное решение первого уравнения, а у₀(х)-общее решение однородного, тогда решением будет их сумма, доказательство делается через производные от этой суммы(y(x)= у₁₊у₀), подставляем и там все получается просто

Т2:Если у₁–частное решение ур-я с правой частью f₁, а у₂аналогично для f2, то решением будет сумма

аналогично доказательству первой тупо берем производные и подставляем,раскидываем и получается верное тождество

Т3: Если правая часть ур-я (1) имеет вид

• 

• 

• 

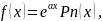
T4: Если правая часть ур-я (1) имеет вид

• 

• 

• 

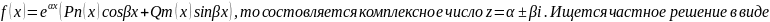
32. Линейные однород. Ур-ния n-го порядка

Теорема: если у1,у2,Yn – частные независимые решения первого уравнения, то общее решение есть сумма типа

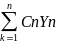
Док-во:

Найдемn производных ф-ии y(x), заданных ф-й 2, если У1, У2…..-линейнонезависимы,

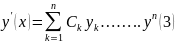
подставляем 3 и 2 в первое:

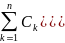=0

=0 (*)

т.к. Yk(x)-частное решение первого уравнения, то

следовательно, в(*) выполняется тождество 0=0

33. Решение линейных дифферен. Ур-ний n-го порядка с постоян коэф.

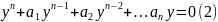
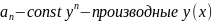
Общее решение ур-я (1)

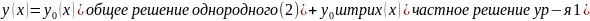
для нахождения частного решения используется метод неопределенных коэф-в

• пусть

• 

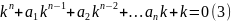
тогда

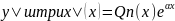
• если является корнем, тогда

• пусть

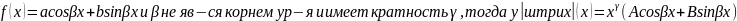
• пусть

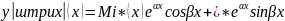, i=max(n,m)

• если f(x) произвольного порядка, то применяется метод вариации постоянных

• если

и общее решение в виде решения однородного+ суммы решений функции(частные решения)

34

35

36. Свойство линейности

Если то .

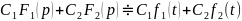Свойство подобия

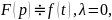то

Доказательство:

,

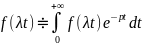замена:

тогда

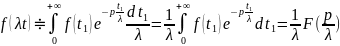
37. Свойства преобразования Лапласа: смещение изображения и запаздывание оригинала.

Смещение изображения (затухание оригинала)

Если то где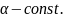

Запаздывание оригинала

Если то

38. Свойства преобразования Лапласа: дифференцирование оригинала и дифференцирование изображения.

Дифференцирование оригинала

Если 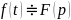и функции 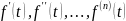— оригиналы, то:

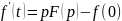
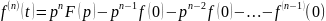
Дифференцирование изображения

Если , то

…

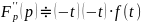
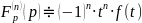
39.

40.

41.

42. Определение функции нескольких переменных

Функция двух переменных — правило, по которому каждой паре значений переменных и 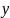из некоторого множества 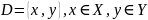соответствует определенное значение величины . Обозначение: или 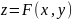, где и — независимые переменные (аргументы), — зависимая переменная (функция).

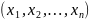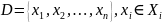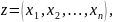Функция переменных — правило, по которому каждому набору из значений переменных из некоторого множества соответствует определенное значение величины . Обозначение: или где 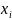— независимые переменные (аргументы), — зависимая переменная (функция).

Способы задания функции двух переменных

1. Аналитический — с помощью формулы. Аналитическая функция двух переменных может быть задана следующими способами:

• Явно:

• Неявно:

• Параметрически:

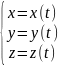
2. Табличный — задание функции с помощью таблицы значений

Область определения функции нескольких переменных

Область определения функции — множество точек, для которых определено значение функции.

Множество значений функции — совокупность значений, которые функция принимает в области определения. Данные определения справедливы как для функции двух переменных, так и для функции n переменных. -окрестность точки — множество точек, удаленных от данной точки на настояние меньшее .

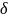Предел функции нескольких переменных

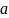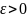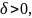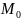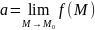Предел функции двух переменных в некоторой точке — число такое, что для любого сколь угодно малого значения найдется такое число что для всех точек из -окрестности точки все соответств. значения функции отличаются от не более чем на : для любых существует хотя бы одно что Обозначение: или