
- •2. Сравнение числовых рядов
- •12. Понятие ортогональной системы действительной функций. Ортогональность основной тригонометрической системы
- •13. Ортогональные системы действительных функций (определение, примеры). Разложение функции по ортогональным системам
- •14. Ряд Фурье. Представление периодической функции в виде ряда Фурье. Сходимость ряда Фурье (теорема Дирихле)
- •15. Разложение в ряд Фурье четных и не четных функций периодических функций. Разложение функций в ряд Фурье, заданной на полупериоде.
- •19. Интеграл Фурье в комплексной форме.
- •20. Теорема о существовании преобразования Фурье
- •21. Синус и косинус преобразования Фурье
- •26. Уравнение Бернулли. Его решение
- •27. Решение линейного диф-го уравнения 1го порядка методом Лагранжа
- •28. Уравнение в полных дифферен. И его решение
- •30. Линейные однородные ур-я 2-го порядка с постоянными коэ-ми. Их решение
- •31. Линейные неоднородные ур-я 2-го порядка с постоянными коэф-ми и правой частью спец. Вида
- •32. Линейные однород. Ур-ния n-го порядка
- •33. Решение линейных дифферен. Ур-ний n-го порядка с постоян коэф.
- •43. Непрерывность функции нескольких переменных
- •44. Частное приращение и частная производная функции нескольких переменных
- •45. Полное приращение функции нескольких переменных
- •47. Касательная плоскость
- •48. Частные производные высших порядков
- •51. Понятие двойного интеграла
- •52.Свойства двойного интеграла
- •53 Теоремы об оценке 2го интеграла
- •54 Техника вычисления 2го интеграла
- •55.Замена переменных в 2ом интеграле
14. Ряд Фурье. Представление периодической функции в виде ряда Фурье. Сходимость ряда Фурье (теорема Дирихле)
Определение ряда Фурье
Говорят, что функция f (x) имеет период P, если f (x + P) = f (x) для всех значений x. Пусть период функцииf (x) равен 2π. В этом случае достаточно рассмотреть поведение функции в интервале [−π, π].
Предположим, что функция f (x) с периодом 2π абсолютно интегрируема в интервале [−π, π]. При этом является конечным так называемый интеграл Дирихле:

Предположим также, что функция f (x) является однозначной, кусочно-непрерывной (то есть имеет конечное число точек разрыва) и кусочно-монотонной (имеет конечное число максимумов и минимумов).
Если
условия 1 и 2 выполнены, то ряд
Фурье для
функции f (x) существует
и сходится к данной функции (Смотрите
об условиях сходимости также
раздел Сходимость
рядов Фурье).
Если x0 −
точка разрыва, то ряд Фурье сходится к
значению
![]()
Ряд
Фурье функции f (x) представляется
в виде
![]()
где коэффициенты Фурье a0, an и bn определяются формулами
![]()
Иногда
используются альтернативные формы
записи для разложения в ряд Фурье.
Заменяя an и bn новыми
переменными dn и φn или dn и θn ,
где
![]()
можно,
соответственно, записать
![]()
Теорема Дирихле. Функция f(x), периодическая с периодом Т = 2l, удовлетворяющая условиям Дирихле на отрезке [-l,l], разлагается в тригонометрический ряд Фурье (53), причем: a) в каждой точке непрерывности х функции f(x) ряд Фурье (53) сходится к значению f(x); b) в каждой точке разрыва хi, функции f(x) ряд Фурье (53) сходится к значению
![]()
15. Разложение в ряд Фурье четных и не четных функций периодических функций. Разложение функций в ряд Фурье, заданной на полупериоде.
Разложение в ряд Фурье четных и нечетных функций
Разложение в ряд Фурье четной функции f (x) с периодом 2π не содержит синусов и имеет вид
![]()
где коэффициенты Фурье определяются выражениями
![]()
Аналогично, разложение в ряд Фурье нечетной функции f (x), имеющей период 2π содержит только синусы и имеет вид
![]()
где ы bn равны
![]()
Ряд Фурье на полупериоде для функций, заданных в интервале L≠2π.
Для подстановки u=πх/L интервал от х=0 до х=L соответствует интервалу от u=0 до u=π. Следовательно, функцию можно разложить в ряд только по косинусам или только по синусам, т.е. в ряд Фурье на полупериоде.
Разложение по косинусам в диапазоне от 0 до L имеет вид
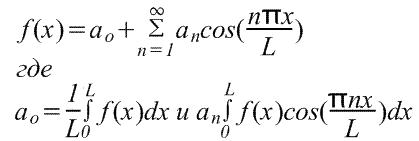
16
17
18. Комплексная форма ряда Фурье. Вывод


Отсюда
 и
и
 .
.

Представим
 и
и
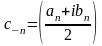 ,
тогда
,
тогда
 комплексная
форма
комплексная
форма
 ,
где
,
где

Ряд Фурье в комплексной форме для функции с произвольным периодом .

 ,
где
,
где
 – гармоники.
– гармоники.
 ,
где
,
где
Волновое
число:

Амплитудный
спектр:
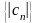

19. Интеграл Фурье в комплексной форме.

Отсюда
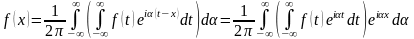 ,
где
,
где
 –
–
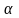 -спектральная
плоскость
-спектральная
плоскость
 .
.
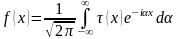 ,
где
,
где
 – преобразования
Фурье для
в комплексной форме.
– преобразования
Фурье для
в комплексной форме.
20. Теорема о существовании преобразования Фурье
Если действительно функция f(x) интегрируема на ох и имеет на ней только точки конечного разрыва, то в точках непрерывности существует ее преобразование Фурье и имеет обратное преобразование Фурье.
….
