Метод комплексной огибающей

Сущность метода сводится к замене реального р/звена моделью низкочастотного звена с входным воздействием в виде комплексной огибающей реального узкополосного сигнала. Метод применяется, как правило, при моделировании на основе принципиальных схем, структурных и функциональных схем. Метод применяется для узкополосных сигналов, у которых ( - ширина спектра, - частота несущей).

Сигнал описывается следующим образом:

.

В общем случае между и нет однозначного соответствия. Неоднозначность можно избежать введением комплексного или аналитического сигнала:

,

- сигнал, сопряженный по Гильберту.

(1)

.

(2)

В заложена вся информация об АМ.

Ф-ла (1) является математической моделью идеального детектора, ф-ла (2) – мат. моделью идеального фазового детектора.

(3)

Ф-ла (3) – математическая модель идеального фазового детектора.

При таком описании сигнала исключается множитель , который является переносчиком информации.

Моделирование по методу комплексной огибающей сводится к разработке алгоритма, связывающего комплексные огибающие на входе и выходе.

Получаемая модель является низкочастотной, так как комплексная огибающая сигнала – это медленно меняющаяся во времени функция.

В методе экономится машинное время и память.

Моделирование процесса преобразования комплексной огибающей сигнала линейной цепью.

Сигнал на выходе связан с входным воздействием: (интеграл Дюамеля):

(4)

- импульсная характеристика цепи.

Для низкочастотного эквивалента цепи можно записать:

(5)

- комплексная импульсная характеристика.

- комплексная огибающая.

Комплексную огибающую на выходе линейной цепи можно промоделировать прямо по формуле (5) (в универсальной ЭВМ, где есть представление комплексных чисел).

В случае (5) по сравнению с (4) количество операций сложения и умножения будет больше. Можно разработать рекурентные соотношения, с помощью которых можно будет моделировать быстрее, но не точнее.

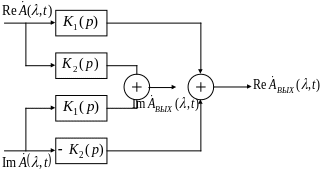
Если в ЭВМ нет представления комплексных чисел, то фильтр с импульсной характеристикой можно будет промоделировать с помощью четырех фильтров, имеющих действительные импульсные характеристики.

 - прямое преобразование Лапласа.

.

Схема вычисления комплексной огибающей на выходе линейной цепи.

.

Чему равна комплексная импульсная характеристика

Реальная цепь

Модель

.

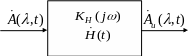
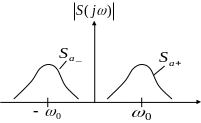
Спектр физического сигнала:

.

,

,

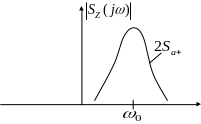
Получили

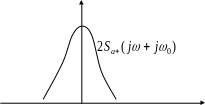
Спектр комплексной огибающей

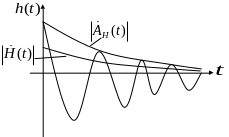
Комплексная импульсная характеристика равна половине комплексной огибающей реальной импульсной характеристики.

Модель резонансного усилителя на основе принципиальной схемы.

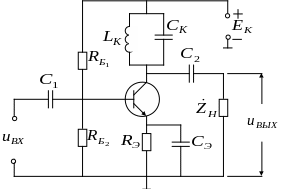
Запишем частотную характеристику

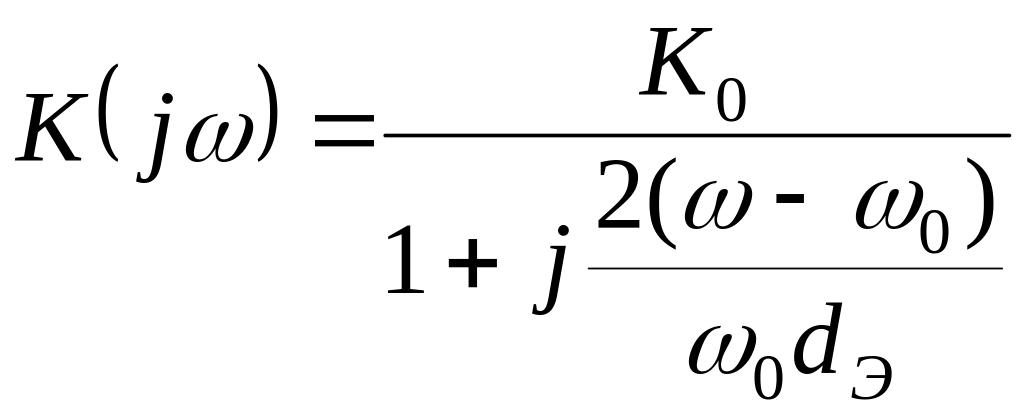
- эквивалентное затухание

- эквивалентная добротность контура.

Запишем укороченную частотную характеристику:

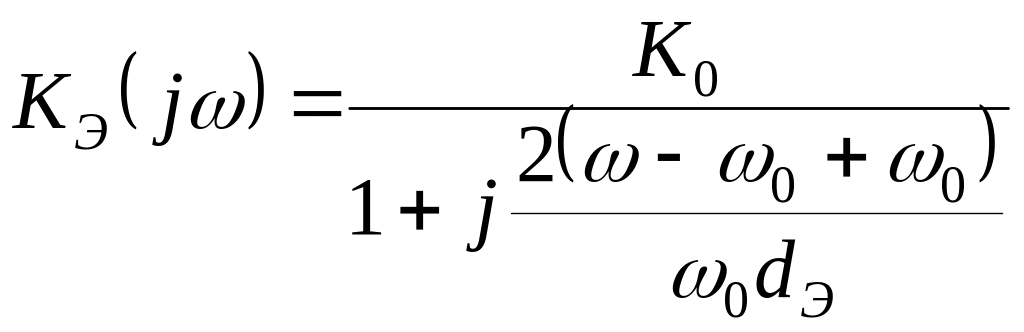
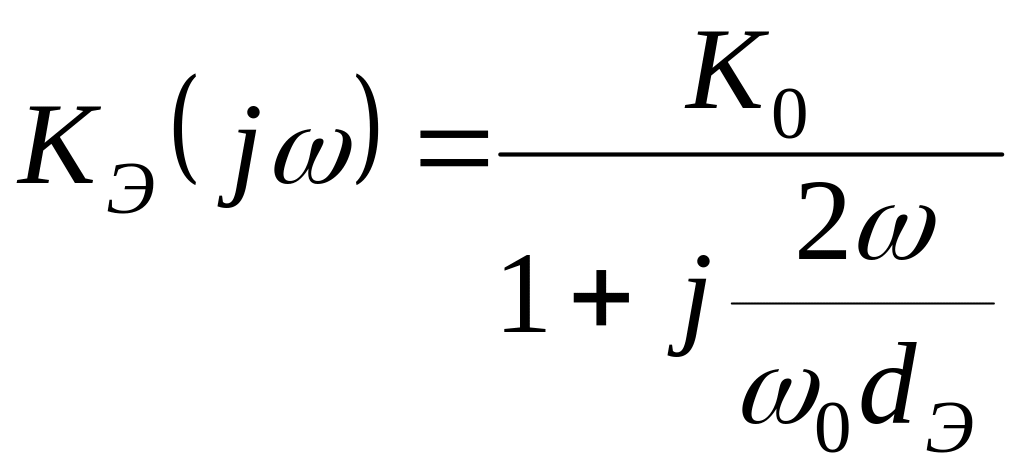
Если ввести обозначение , получим (*)

Инерционное звено .

Тогда для ф-лы (*) получим