44. Связь задач сортировки и поиска.

Поиск и сортировка часто связаны между собой.

A = {a1,… am}

B = {b1,… bn}

Является ли мн-во А подмножеством мн-ва B.

1. сравнить каждое аi последовательно со всеми bi до нахождения совпадения.

2. сначала рассортировать мн-во А и В и сделать 1 проход с проверкой по этим мн-вам.

3. внести все эл. Bj в таблицу и затем выполнить поиск для каждого значения ai.

45. Последовательный поиск.

b1,…bn

k1,…kn

n >= 1

Найти запись с ключом К

При последовательном поиске подразумевают рассмотрение ключей в том порядке, в кот. они встречаются в таблице. При таком поиске в худшем случае мы получаем просмотр всей таблицы. И последовательный поиск как правило имеет число операций пропорциональных n.

Для малых эл-ов – быстрый. Для больших таблиц – медленный.

Это единственный метод поиска, кот. можно применить для неупорядоченных ключей.

Последовательно сравниваем значение К с ключами К1 … Кn

Если нашли К = Ki, то успешно, иначе – запись не сущ.

i = нач. знач.

if К = Ki – yes

if I = n – no

I = I + 1

46. Быстрый последовательный поиск.

Для ускорения работы цикла общим приемом является добавление в таблицу спец. строки.

Она дает возможность не делать проверки, достигли ли мы конца таблицы.

В конец таблицы добавляется фиктивная запись с К. Тогда цикл всегда будет завершаться нахождением ключа К и не придется каждый раз осуществлять проверку i = n

После окончания цикла однократно выполняемые проверки условия I > n скажет о том, что является найденный ключ истинным или фиктивным.

В некоторую запись bn+1 после ключа = К

I = нач. знач.

if k = ki – то возможно запись найдена, иначе i++

Добавить фиктивную запись можно в том случае, если мы имеем прямой непосредственный доступ к концу таблицы.

47. Последовательный поиск в упорядоченной таблице. Поиск путем сравнения ключей.-херня!

Последовательный поиск. "Начать с начала и продолжать, пока не будет найден искомый ключ; затем оста­новиться". Эта последовательная процедура представляет собой очевидный путь поиска и может служить отличной отправной точкой для рассмотрения множества алгоритмов поиска, поскольку они основаны на последовательной процедуре. Ниже представлена более точная формулировка алгоритма. Алгоритм S (Последовательный поиск (Sequential search)). Дана таблица записей R1, R2,..., Rn с ключами К1, К2,..., Kn соответственно. Алгоритм предназначен для поиска записи с заданным ключом К. Предполагается, что N > 1. S1.  [Инициализация.] Установить i := 1. S2.  [Сравнение.] Если К = Кi, алгоритм заканчивается успешно. S3.  [Продвижение.] Увеличить i на 1. S4.  [Конец массива] Если i <  N, перейти к шагу S2. В противном случае алгоритм заканчивается неудачно.

/*b1… bn

k1<… <kn

K

При нахождении первого ключа >= K завершается поиск. – эл. не найден. ПОЧЕМУ ?

Методы:

1. метод деления пополам (логарифмический)

2. интерполяционный (Kn - Kl) / (K - Kl)

Часто методы комбинируют. На ранних стадиях исп. интерполяцион. поиск.*/

48. Бинарный поиск. Интерполяционный поиск.

На практике довольно часто производится поиск в массиве, элементы которого упорядочены по некоторому критерию. Например, массив фамилий, как правило, упорядочен по алфавиту, массив данных о погоде — по датам наблюдений. В случае, если массив упорядочен, то применяют другие, более эффективные по сравнению с методом простого перебора алгоритмы, например – метод бинарного поиска. Идея: в процессе поиска границы  промежутка  сдвигаются  друг  к другу, причем  после  каждого  сравнения  изменяется только одна граница: либо верхняя,  либо нижняя. Алгоритм, использующий последовательное уменьшение промежутка в 2 раза, также называется  дихотомия (деление пополам). Обозначим: No - номер наименьшего элемента последовательности; Nk - номер наибольшего элемента последовательности; i – средний (по номеру) элемент в массиве. Алгоритм бинарного поиска реализуется следующим образом: 1. Сначала образец сравнивается со средним (по номеру) элементом массива.

• Если образец равен среднему элементу, то задача решена.

• Если образец больше среднего элемента, то это значит, что искомый элемент расположен правее среднего элемента (между элементами с номерами i+1 и Nk), и за новое значение No принимается i+1, а значение Nk не меняется.

• Если образец меньше среднего элемента, то это значит, что искомый элемент расположен левее среднего элемента (между элементами с номерами No и i-1), и за новое значение Nk принимается i-1, а значение No не меняется.

2. После того как определена часть массива, в которой может находиться искомый элемент, по формуле (Nk + N0)  div 2 вычисляется новое значение i и поиск продолжается.

Основой алгоритма является цикл, выполняемый неопределенное количество раз. В этом цикле интервал номеров делится пополам,  получается номер под названием INDEX.  Элемент с этим номером сравнивается с поисковой переменной Р. В зависимости от результата сравнения:  перевычисляется No или Nk. Это повторяется до тех пор,  не обнаружится элемент или No и Nk не совпадут,  затем  делается проверка X[No]=Р и по ее исходу формируется результат.

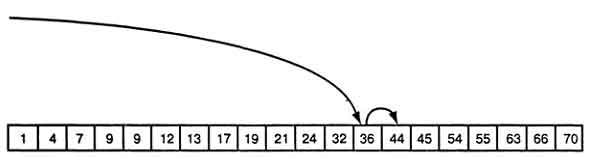
Двоичный поиск. Последовательный поиск вы­полняется очень быстро для небольших объёмов информации. Большие – намного быст­рее обрабатывает алгоритм двоичного поиска. Алгоритм двоичного поиска сравнивает элемент в середине списка с искомым. Если искомый элемент меньше, алгоритм продолжает перебирать первую половину списка, если же он больше, чем найденный элемент, поиск продолжается во второй половине списка. На рисунке процесс поиска элемента со значением 44 изображен графически.    

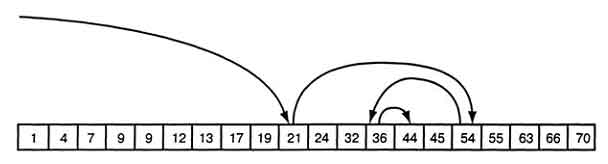
Интерполяционный поиск. Двоичный поиск оптимизирует поиск полным перебором, так как исключает большие части списка, не проверяя значения пропускаемых элементов. Если изве­стно, что значения распределены достаточно равномерно, то можно на каждом шаге исключить еще большее количество элементов, используя интерполяционный поиск. Интерполяция - это процесс предсказания неизвестных значений на основе имеющихся. В данном случае вы используете индексы известных значений в спис­ке, чтобы определить, какой индекс должно иметь искомое значение. Предполо­жим, что вы имеете такой же список. Этот список содержит 20 элементов со значениями от 1 до 70. Допустим, что вы хотите найти в этом списке элемент со значением 44. Значение 44 составляет 64% размера диапазона от 1 до 70. Если считать, что значения элементов распределены равномерно, то искомый элемент, предположительно, будет находиться в позиции, составляющей 64% от размера списка - то есть в позиции с индексом 13. Если найденная алгоритмом позиция неверна, то он сравнивает искомое зна­чение со значением в выбранной позиции. Если искомое значение меньше, алго­ритм продолжает искать элемент в первой части списка, если больше, то поиск продолжается во второй части списка. На рисунке графически представлен про­цесс интерполяционного поиска.