Вопрос 12.

Однородные системы. Фундаментальные системы решений.

Векторная алгебра.

Вопрос 1.

Понятие вектора. Линейные опереции над векторами: сложение векторов и умножение на число. Линейные свойства векторов. Примеры.

Вектор-направленный отрезок

, А-начало вектора

В-конец вектора

Длина вектора-

Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых.

Нулевой вектор коллинеарен любому вектору.

Векторы называются компланарными, если существует плоскость, которой они параллельны. Коллинеарные векторы всегда компланарны, но не все компланарные векторы коллинеарны.

Векторы называются равными, если они коллинеарны, сонаправлены и имеют одинаковые модули.

Всякие векторы можно привести к общему началу, т. е. построить векторы, равные данным и имеющие общее начало.

Линейными операциями над векторами являются сложение и умножение на число.

Суммой векторов

Произведением векторов

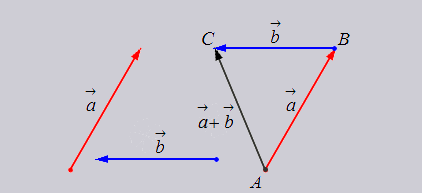Сумма векторов по правилу треугольника

По правилу параллелограмма

Свойства векторов:

 +   =   +      - коммутативность;

 + (  +  ) = (  +  ) +      - ассоциативность (по сложению);

    +   =   ;

 1 ×   =  ;

   + (- ) =   -   =   + (-1)  =  ;

α(β ) = (αβ)     - ассоциативность (по отношению к числам);

(α + β)  = α  + β     - дистрибутивность (по отношению к умножению на вектор);

α(  +  ) = α  + α     - дистрибутивность (по отношению к умножению на число).

   α, β - числа.

Свойства линейнонезависимых и линейнозависимых векторов:

1. Если к линейно зависимой системе векторов   добавить несколько векторов, то полученная система будет линейно зависимой.

2. Если из линейно независимой системы векторов   исключить несколько векторов, то полученная система будет линейно независимой.

3. Если в системе векторов   есть хотя бы один нулевой вектор, то такая система линейно зависимая.

4. Если система векторов   линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов   линейно независима, то ни один из векторов не выражается через остальные.

Вопрос 2 .

Проекция вектора на ось. Проекцией вектора на ось называется вектор, который получается в результате перемножения скалярной проекции вектора на эту ось и единичного вектора этой оси. Например, если а_x – скалярная проекция вектора а на ось X, то а_x·i - его векторная проекция на эту ось.  Обозначим  векторную проекцию также, как и сам вектор, но с индексом той оси на которую вектор проектируется. Так, векторную проекцию вектора а на ось Х обозначим  а_x (жирная буква, обозначающая вектор и нижний индекс названия оси) или   (нежирная буква, обозначающая вектор, но со стрелкой наверху (!) и нижний индекс названия оси). 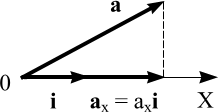Скалярной проекцией вектора на ось называется число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция. Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектора, то его проекция обозначается а_x. При проектировании этого же вектора на другую ось, если  ось Y , его проекция будет обозначаться а_y . Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть а_x = х_к − x_н. Проекция вектора на ось - это число. Причем, проекция может быть положительной, если величина х_к больше величины х_н,  отрицательной,  если величина х_к меньше величины х_н  и равной нулю, если х_к равно х_н . 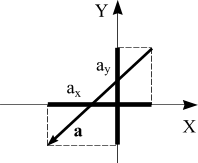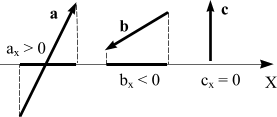Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью.  Из рисунка  видно, что а_x = а Cos α то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора. Если угол острый, то  Cos α > 0 и а_x > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна. 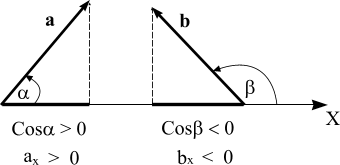Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу - отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против. Чтобы найти проекцию вектора на ось надо модуль этого вектора умножить на косинус угла между направлением оси и направлением вектора.

Вначале вспомним, что такое ось, проекция точки на ось и координата точки. Ось – это прямая, которой придается какое–то направление. Можете считать, что это вектор с бесконечно большим модулем. Ось обозначается какой-либо буквой: X , Y , Z , s , t … Обычно на оси выбирается (произвольно) точка, которая называется началом отсчета и, как правило, обозначается буквой О. От этой точки отсчитываются расстояния до других интересующих нас точек. Проекция точки на ось - это основание перпендикуляра, опущенного из этой точки на данную ось (рис. 8). То есть, проекцией точки на ось является точка.

Рис. 8

Координата точки - это число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между началом оси и проекцией точки на эту ось. Это число берется со знаком плюс, если проекция точки располагается в направлении оси от ее начала и со знаком минус, если в противоположном направлении. Скалярная проекция вектора на ось - это число, абсолютная величина которого равна длине отрезка оси (в выбранном масштабе), заключённого между проекциями точки начала и точки конца вектора. Обычно вместо выражения скалярная проекция говорят просто – проекция, то есть слово скалярная опускают. Проекция обозначается той же буквой, что и проектируемый вектор (в обычном, нежирном написании), с нижним (как правило) индексом названия оси, на которую этот вектор проектируется. Например, если на ось Х проектируется вектор а, то его проекция обозначается а_x. При проектировании этого же вектора на другую ось, скажем, ось Y , его проекция будет обозначаться а_y (рис. 9).

Рис. 9

Чтобы вычислить проекцию вектора на ось (например, ось X) надо из координаты точки его конца вычесть координату точки начала, то есть

а_x = х_к − x_н.

Надо помнить: проекция вектора на ось - это число! Причем, проекция может быть положительной, если величина х_к больше величины х_н, отрицательной, если величина х_к меньше величины х_н и равной нулю, если х_к равно х_н (рис. 10).

Рис. 10

Проекцию вектора на ось можно также найти, зная модуль вектора и угол, который он составляет с этой осью. Из рисунка 11 видно, что а_x = а Cos α то есть, проекция вектора на ось равна произведению модуля вектора на косинус угла между направлением оси и направлением вектора. Если угол острый, то Cos α > 0 и а_x > 0, а, если тупой, то косинус тупого угла отрицателен, и проекция вектора на ось тоже будет отрицательна.

Рис. 11

Углы, отсчитываемые от оси против хода часовой стрелки, принято считать положительными, а по ходу - отрицательными. Однако, поскольку косинус – функция четная, то есть, Cos α = Cos (− α), то при вычислении проекций углы можно отсчитывать как по ходу часовой стрелки, так и против. При решении задач часто будут использоваться следующие свойства проекций: если а = b + c +…+ d , то а_x = b_x + c_x +…+ d_x (аналогично на другие оси), если a = mb, то а_x = mb_x (аналогично на другие оси).

Координаты и компоненты вектора

Если и — два неколлинеарных вектора в плоскости, а — произвольный вектор в той же плоскости, то всегда существуют такие числа и , что . В этом случае говорят, что вектор разложен по векторам и .

Если и — неколлинеарные единичные векторы (т. е. вектора, модуль которых равен единице) , то произвольный вектор плоскости может быть представлен в виде . В этом случае говорят, что вектор имеет в системе и координаты .

Если векторы и взаимно перпендикулярны, причем вектор может быть получен из вектора поворотом против часовой стрелки, то говорят, что прямые, в которых лежат и , образуют декартову прямоугольную систему координат, а числа называются декартовыми координатами вектора .

Пусть точка с координатами — начало вектора , а точка с координатами — его конец. Тогда координаты вектора связаны с координатами точек и формулами: , , т. е. декартовы координаты вектора равны разности соответствующих координат конца вектора и его начала.

Декартовы координаты вектора являются проекциями этого вектора на соответственные оси систем координат: , .

Пусть вектор имеет координаты , что записывается в виде , а вектор — , или .

Тогда:

,

,

,

,

т. е. действиям с векторами отвечают идентичные действия с их координатами.

Модуль вектора определяется через его декартовы координаты посредством равенства: , а единичный вектор , имеющий с вектором одинаковое направление, записывается в виде и имеет координаты: .

Линейные операции над векторами

Определение. Линейными операциями над векторами называется сложение и умножение на число.

            Суммой векторов является вектор -

            Произведение - , при этом  коллинеарен .

Вектор  сонаправлен с вектором ( ­­), если  > 0.

Вектор  противоположно направлен с вектором (­), если  < 0.