Вопрос 11.

Вывод уравнения прямой в пространстве, проходящей через две данные точки. Пример.

  Если на прямой в пространстве отметить две произвольные точки M₁(x₁, y₁, z₁) и M₂(x₂, y₂, z₂), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:

.

  Кроме того, для точки М₁ можно записать:

.

 Решая совместно эти уравнения, получим:

.

Это уравнение прямой, проходящей через две точки в пространстве.

Пример: Найти уравнение прямой, проходящей через две точки: (-1, 2) и (2, 1).

Решение.По уравнению

полагая в нем x₁ = -1, y₁ = 2, x₂ = 2, y₂ = 1 (без разницы, какую точку считать первой, какую - второй), получим

или

после упрощений получаем окончательно искомое уравнение в виде x + 3y - 5 = 0.

Вопрос 12.

Общее уравнение прямой в пространстве.Переход от общего уравнения к каноническому.

Переход от общих уравнений прямой к каноническим или параметрическим уравнения

Для того, чтобы от общих уравнений  перейти к каноническим или параметрическим уравнениям прямой, требуется найти направляющий вектор  этой прямой и координаты любой точки , принадлежащей ей. Направляющий вектор прямой ортогонален нормалям  и  к обеим плоскостям, следовательно,  коллинеарен их векторному произведению . Поэтому в качестве   направляющего вектора можно выбрать   или любой вектор с пропорциональными координатами. Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно, а две остальные   найти из уравнений , выбрав их так, чтобы определитель из их коэффициентов не равнялся нулю. Пример. Составить канонические и параметрические уравнения прямой  . Решение. По условию , тогда . Следовательно, направляющим вектором прямой можно считать вектор . Будем искать точку на прямой с координатой . Для координат  и  получим систему уравнений , откуда  , . Теперь можно составить канонические уравнения прямой:   .

 

Вопрос 16.

Канноническое уравнение эллипса

эллипсом – называется геометрическое место точек на плоскости, сумма расстояний которых до двух заданных точек, называемых фокусами, есть, величина постоянная, большая чем расстояние между фокусами.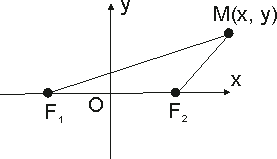 Комментарии к определению: F1 и F2 – фокусы, | F1F2 | = 2·с — расстояние между фокусами, | MF1 | + |MF2| = 2·a >2·c — определение эллипс Система координат, в которой уравнение имеет наиболее простой вид, называется канонической. Проведём ось абсцисс через фокусы, начало координат поместим в середине между фокусами, ось ординат направим перпендикулярно. Пусть М(х, у) — произвольная точка на эллипсе, тогда F1(- c; 0) и F2(c; 0). Расстояния текущей точки эллипса до её фокусов называются фокальными расстояниями |MF1| = r1, |MF2| = r2 и, по определению эллипса, имеем r1 + r2 = 2·a. Воспользовавшись формулой расстояния между двумя точками, из определения эллипса имеем:

В итоге

получим каноническое уравнение эллипса

.

Эксцентрисит эллипса

Определение. называется отношение c ⁄ a, где с — половина расстояния между фокусами, а — большая полуось эллипса.Эксцентриситет обозначают буквой ε: ε = c⁄ a.

Из равенства легко получается геометрическое истолкование эксцентриситета эллипса. При очень малом ε числа а и b почти равны, т.е. эллипс близок к окружности. Если же ε близко к единице, то число b весьма мало по сравнению с числом а и эллипс сильно вытянут вдоль большой оси. Эксцентриситет эллипса характеризует меру вытянутости эллипса.

Соотношения для фокальных расстояний эллипсаУбедимся в том, что если координаты точки удовлетворяют каноническому уравнению эллипса, то сумма расстояний этой точки до двух точек, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами. Для этого, очевидно, достаточно показать, что величины r1 и r2 для любой точки, координаты которой удовлетворяют уравнению эллипса, удовлетворяют соотношению r1 + r2= 2·a.

Так как по определению с < a и | х | < a, то выражение в скобках под знаком корня положительно, поэтому

Аналогично найдём

Складывая фокальные расстояния, получим r1 + r2 = 2·aЧто и требовалось доказать. Таким образом, эллипс — линия второго порядка. Замечание. Если а = b, то уравнение эллипса принимает вид x2 + y2= a2. Это уравнение окружности радиуса а. Т.О. окружность — частный случай эллипса. Заметим, что эллипс можно получить из окружности радиуса а, если сжать ее в а ⁄ b раз вдоль оси Оу. Оси симметрии эллипса называются его осями, а центр симметрии (точка пересечения осей) — центром эллипса. Точки, в которых эллипс пересекает оси, называются его вершинами. Вершины ограничивают на осях отрезки, равные 2·а и 2·b. Если а ≥ b, величины а и b называются соответственно большой и малой полуосями эллипса.

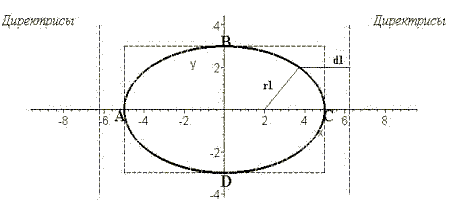
Директрисы эллипса

Определение. Две прямые, перпендикулярные большой оси эллипса и расположенные симметрично относительно центра на расстоянии а⁄ ε от него, называются директрисами эллипса (здесь, а — большая полуось, ε — эксцентриситет эллипса).Так как для эллипса ε < 1, то a ⁄ ε > a. Отсюда следует, что правая директриса расположена правее правой вершины эллипса, а левая — общее свойство, присущее эллипсу.

Аналогично доказывается для левого фокуса эллипса.