Линейная алгебра. Вопрос 1

Определители и их свойства

Определитель квадратной матрицы (2x2)- разность произведений элементов главной и побочной диагонали

Определитель квадратной матрицы (3x3)

Определитель квадратной матрицы n-ого порядка называется число, равное алгебраической суммы n! Членов, каждое из которых является произведением n элементов матрицы, взятых по одному из каждой строки каждого столбца, причем знак каждого члена определяется как элементов матрицы

Свойства определителей

1. Определитель не изменится, если его строки поменять местами с соотв. Столбцами, т.е. транспонировать

2. При перестановке 2-х строк или столбцов определитель изменит свой знак на противоположный

3. Общий множитель строки или столбца можно внести за знак определителя

4. Определитель с 2-умя одинаковыми строками или столбцами равен 0

5. Если все элементы 2-х строк или столбцов определителя пропорциональны, то определитель равен 0

6. Если к какой-либо строке или столбцу определителя прибавить соотв.элементы другой строки или столбца умноженные на одно и то же число, то определитель не изменит свей величины

7. Треугольный определитель, у которого все элементы лежащей выше или ниже гл.диагонали равен произведению элементов главной диагонали

8. Если матрица состоит из нулей, то ее определитель равен 0

Вопрос 3

Матрицы: определение, виды матриц

Матрицей рзмера mxn? Где m- число строк, n – число столбцов называется таблица чисел, расположенных в определенном порядке. Эти числа называются элементами матрицы. Место каждого элемента однозначно определено номером строки и столбца на пересечении которых он находится. Элементы матрицы обозначаются

a ij, i – номер строки, j – номер столбца

Основные действия над матрицами:

Матрица может состоять из одной строки А=(1 3 5),

из одного столбца

из одного элемента В=(5)

Если число столбцов равно числу строк, то матрица называется квадратной

Матрица, все элементы которой равны нулю, называется нулевой

Матрица вида называется единичной

Если amn = anm, то матрица называется симметричной

Квадратная матрица вида 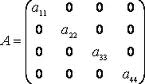называется диагональной

Вопрос 4.

Действия над матрицами: свойства операций.

Основные действия над матрицами:

При сложении и вычитании матрицы должны быть одного размера. Операция умножения(деления) матрицы любого размера на любое число сводится к умножению(делению) каждого элемента матрицы на это число.

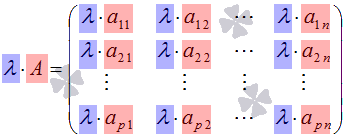
Сложение матриц: А+В=В+А; α(А+В)=  αА+ αВ

Суммой двух матриц   и   является матрица, элементы которой равны сумме соответствующих элементов матриц А и В, то есть,  .

Таким образом, результатом сложения двух матриц является матрица того же порядка. Свойства операции сложения матриц. 1.Для матриц А, В и С одного порядка характерно свойство ассоциативности сложения А + (В + С) = (А + В) + С.

2.Для матриц данного порядка существует нейтральный элемент по сложению, которым является нулевая матрица. То есть, справедливо свойство А + О = А.

3.Для ненулевой матрицы А данного порядка существует матрица ( – А ), их суммой является нулевая матрица: А + ( - А ) = О.

4.Для матриц А и В данного порядка справедливо свойство коммутативности сложения А + В = В + А.

Операция умножения матриц. Произведением матриц называется матрица, элементы которой могут быть вычислены по формуле:

Свойства операций умножения матриц. Чтобы найти элемент первой строки и первого столбца необходимо каждый элемент первой строки матрицы А умножить на соответствующий элемент первого столбца матрицы В и полученные результаты сложить. 1) Умножение матриц не коммуникативно А*В не равно В*А Матрица А умножить на единичную матрицу Е = матрица А Матрица А умножить на нулевую матрицу О=0 2)Операция перемножения матриц ассоциативна А*(В*С)=(А*В)*С

3)Операция умножения матриц дистрибутивна по отношению к сложению. А*(В+С)=А*В+А*С 4)Если произведение А*В определено, то для любого числа α верно соотношение α (А*В)=( α *А)*В=А*( α *В)

5)Если определено произведение матриц А*В, то определено произведение В^Т *А^Т

(А*В) ^Т = В^Т *А^Т , где индексом Т определена транспонированная матрица. Матрица В называется транспонированной матрице А, а переход от А к В –транспонированием, если элемент каждой строки матрицы А записать в том же порядке в столбцы матрицы В. Операция умножения двух матриц. Операция умножения двух матриц А и В определена, когда ЧИСЛО СТОЛБЦОВ МАТРИЦЫ А РАВНО ЧИСЛУ СТРОК МАТРИЦЫ В. Произведением матрицы А порядка   на матрицу В порядка   является такая матрица С порядка  , каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-ого столбца матрицы В, то есть,

Таким образом, результатом умножения матрицы порядка   на матрицу порядка   является матрица порядка  .