
- •8 Вопрос
- •9 Вопрос Координаты вектора
- •Свойства
- •Модуль вектора
- •10 Вопрос Скалярное произведение векторов
- •11 Вопрос Формула для вычисления скалярного произведения векторов через их координаты.
- •Формула для вычисления угла между векторами.
- •12 Вопрос
- •13 Вопрос
- •14 Вопрос
- •15 Вопрос
- •16 Вопрос
- •17 Вопрос Расстояние от точки до прямой
- •Теорема доказана.
- •18 Вопрос
- •Окружность
- •19 Вопрос Гипербола
- •20 Вопрос Парабола
- •21 Вопрос числовые последовательности VI
- •§ 129. Ограниченные и неограниченные числовые последовательности
- •22 Вопрос Бесконечно малая величина
- •23 Вопрос Определение
- •Обозначения
- •Свойства
- •Свойства Арифметические свойства
- •Свойства сохранения порядка
- •Другие свойства
- •24 Вопрос
- •Промежутки монотонности
- •26 Вопрос Непосредственное вычисление пределов, таблица пределов функций.
- •27 Вопрос Предел функции
- •Свойства пределов функции
- •28 Вопрос
- •1. Непрерывность функции в точке.
- •29 Вопрос Свойства функций, непрерывных на отрезке
- •30 Вопрос
- •Определение производной функции через предел
Промежутки монотонности
Может
оказаться, что вышеуказанные условия
выполняются не для всех номеров
![]() ,
а лишь для номеров из некоторого диапазона
,
а лишь для номеров из некоторого диапазона
![]()
(здесь
допускается обращение правой границы
![]() в
бесконечность). В этом случае
последовательность называется монотонной
на промежутке
в
бесконечность). В этом случае
последовательность называется монотонной
на промежутке
![]() ,
а сам диапазон
называется
промежутком монотонности
последовательности.
,
а сам диапазон
называется
промежутком монотонности
последовательности.
Mонотонные и ограниченные последовательности. Число е.
Последовательность
![]() называется
называется
возрастающей, если
 ,
,
убывающей, если
 .
.
Возрастающие
и убывающие последовательности называются
монотонными.
Последовательность
называется
ограниченной
сверху,
если все члены последовательности
![]() .
Последовательность
называется
ограниченной
снизу,
если все члены последовательности
.
Последовательность
называется
ограниченной
снизу,
если все члены последовательности
![]() .
Последовательность
называется
ограниченной, если она ограничена и
сверху, и снизу.
Пример: исследовать
последовательность
.
Последовательность
называется
ограниченной, если она ограничена и
сверху, и снизу.
Пример: исследовать
последовательность
 на
монотонность и ограниченность.
Решение:
на
монотонность и ограниченность.
Решение:
 ограничена
снизу. (Если
ограничена
снизу. (Если
 )
)
 убывает,
поэтому
ограничена
сверху.
убывает,
поэтому
ограничена
сверху.
Ответ:
последовательность ограничена и
монотонно убывает.
Теорема
Вейерштрасса:
Монотонная и ограниченная последовательность
имеет предел.
Число
е.
Последовательность
![]()
возрастает

ограничена:
 по
теореме Вейерштрасса
по
теореме Вейерштрасса
 .Его
обозначают буквой e
и называют числом
e.
.Его
обозначают буквой e
и называют числом
e.
26 Вопрос Непосредственное вычисление пределов, таблица пределов функций.
Непосредственное
вычисление пределов
основано на определении непрерывности
функции в точке,
на определении предела функции на
бесконечности и на использовании свойств
предела непрерывной
функции.
Утверждение.
Значение
предела в точке непрерывности функции
равно значению функции в этой точке.
То
есть, для основных
элементарных функций (и
функций полученных из основных
элементарных с помощью элементарных
преобразований графиков), опираясь на
их известные свойства, предел в любой
точке из области определения, кроме
граничных, можно вычислять как значение
соответствующей функции в этих
точках.
Пример.
Вычислить
предел
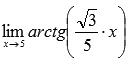 Решение.
Так
как функция арктангенса непрерывна на
всей области определения, то она
непрерывна и в точке
Решение.
Так
как функция арктангенса непрерывна на
всей области определения, то она
непрерывна и в точке
![]() .
Следовательно, значение предела равно
значению функции в этой точке.
.
Следовательно, значение предела равно
значению функции в этой точке.
 В
граничных точках области определения
вычисляются односторонние
пределы.
Например, для арксинуса и арккосинуса
при
В
граничных точках области определения
вычисляются односторонние
пределы.
Например, для арксинуса и арккосинуса
при
![]() или
или
![]() .
На
плюс или минус бесконечности вычисляются
соответствующие пределы при
.
На
плюс или минус бесконечности вычисляются
соответствующие пределы при
![]() или
или
![]() на
основании определеня предела функции
на бесконечности.
Самые
используемые свойства
пределов.
на
основании определеня предела функции
на бесконечности.
Самые
используемые свойства
пределов.
 ,
где k
– коэффициент.
,
где k
– коэффициент.
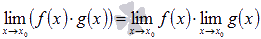 ,
если в результате не выходит одна из
неопределенностей
пределов.
,
если в результате не выходит одна из
неопределенностей
пределов.
Для непрерывных функций знак предельного перехода и знак функции можно менять местами:

Массу пределов можно вычислить зная свйства основных элементарных функций. Приведем значение пределов этих функций в таблице, а ниже дадим разъяснения и несколько примеров с решениями. Все значения можно вычислить основываясь на определении предела функции в точке и на бесконечности. Таблица пределов функций Держите эту таблицу основных пределов перед глазами при решении задач и примеров. Она значительно упростит Вам жизнь.





