
- •8 Вопрос
- •9 Вопрос Координаты вектора
- •Свойства
- •Модуль вектора
- •10 Вопрос Скалярное произведение векторов
- •11 Вопрос Формула для вычисления скалярного произведения векторов через их координаты.
- •Формула для вычисления угла между векторами.
- •12 Вопрос
- •13 Вопрос
- •14 Вопрос
- •15 Вопрос
- •16 Вопрос
- •17 Вопрос Расстояние от точки до прямой
- •Теорема доказана.
- •18 Вопрос
- •Окружность
- •19 Вопрос Гипербола
- •20 Вопрос Парабола
- •21 Вопрос числовые последовательности VI
- •§ 129. Ограниченные и неограниченные числовые последовательности
- •22 Вопрос Бесконечно малая величина
- •23 Вопрос Определение
- •Обозначения
- •Свойства
- •Свойства Арифметические свойства
- •Свойства сохранения порядка
- •Другие свойства
- •24 Вопрос
- •Промежутки монотонности
- •26 Вопрос Непосредственное вычисление пределов, таблица пределов функций.
- •27 Вопрос Предел функции
- •Свойства пределов функции
- •28 Вопрос
- •1. Непрерывность функции в точке.
- •29 Вопрос Свойства функций, непрерывных на отрезке
- •30 Вопрос
- •Определение производной функции через предел
Ответы по высшей математике на вопросы
7 вопрос
Ме́тод Га́усса[1] — классический метод решения системы линейных алгебраических уравнений (СЛАУ). Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные[2].
Описание метода
Пусть исходная система выглядит следующим образом
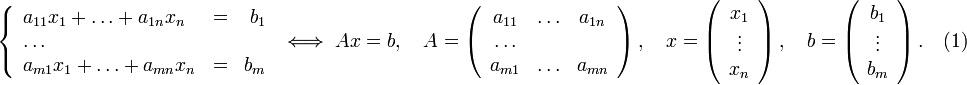
Матрица
![]() называется
основной матрицей системы,
называется
основной матрицей системы,
![]() —
столбцом свободных членов.
—
столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду(эти же преобразования нужно применять к столбцу свободных членов):
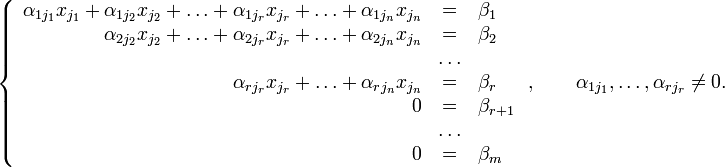
При
этом будем считать, что базисный
минор
(ненулевой минор
максимального порядка) основной матрицы
находится в верхнем левом углу, то есть
в него входят только коэффициенты при
переменных
![]() [3].
[3].
Тогда переменные называются главными переменными. Все остальные называются свободными.
Если
хотя бы одно число
![]() ,
где
,
где
![]() ,
то рассматриваемая система несовместна.
,
то рассматриваемая система несовместна.
Пусть
![]() для
любых
.
для
любых
.
Перенесём
свободные переменные за знаки равенств
и поделим каждое из уравнений системы
на свой коэффициент при самом левом
![]() (
(![]() ,
где
,
где
![]() —
номер строки):
—
номер строки):
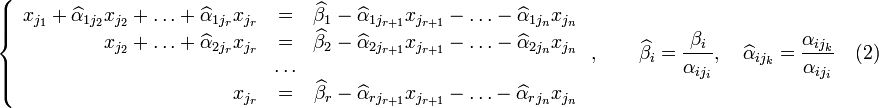 ,
где
,
где
![]()
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.
|
Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой. 2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной. |
|
Условие совместности
Упомянутое
выше условие
для
всех
![]() может
быть сформулировано в качестве
необходимого и достаточного условия
совместности:
может
быть сформулировано в качестве
необходимого и достаточного условия
совместности:
Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны).
|
Теорема Кронекера-Капелли. Система совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Следствия:
|
|
Алгоритм
Описание
Алгоритм решения СЛАУ методом Гаусса подразделяется на два этапа.
На первом этапе осуществляется так называемый прямой ход, когда путём элементарных преобразований над строками систему приводят к ступенчатой или треугольной форме, либо устанавливают, что система несовместна. А именно, среди элементов первого столбца матрицы выбирают ненулевой, перемещают его на крайнее верхнее положение перестановкой строк и вычитают получившуюся после перестановки первую строку из остальных строк, домножив её на величину, равную отношению первого элемента каждой из этих строк к первому элементу первой строки, обнуляя тем самым столбец под ним. После того, как указанные преобразования были совершены, первую строку и первый столбец мысленно вычёркивают и продолжают пока не останется матрица нулевого размера. Если на какой-то из итераций среди элементов первого столбца не нашёлся ненулевой, то переходят к следующему столбцу и проделывают аналогичную операцию.
На втором этапе осуществляется так называемый обратный ход, суть которого заключается в том, чтобы выразить все получившиеся базисные переменные через небазисные и построить фундаментальную систему решений, либо, если все переменные являются базисными, то выразить в численном виде единственное решение системы линейных уравнений. Эта процедура начинается с последнего уравнения, из которого выражают соответствующую базисную переменную (а она там всего одна) и подставляют в предыдущие уравнения, и так далее, поднимаясь по «ступенькам» наверх. Каждой строчке соответствует ровно одна базисная переменная, поэтому на каждом шаге, кроме последнего (самого верхнего), ситуация в точности повторяет случай последней строки.
Метод
Гаусса требует порядка
![]() действий.
действий.
Этот метод опирается на:
|
Теорема (о приведении матриц к ступенчатому виду). Любую матрицу путём элементарных преобразований только над строками можно привести к ступенчатому виду. |
|
Простейший случай
В
простейшем случае алгоритм выглядит
так:
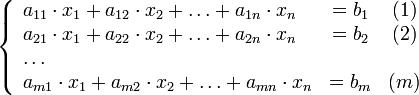
Прямой ход:
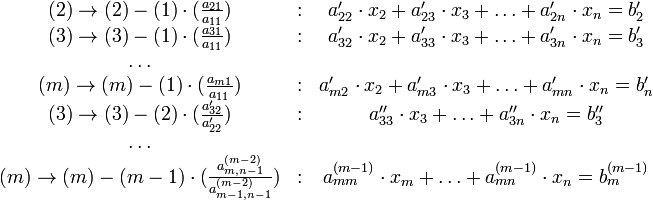
Обратный ход. Из последнего ненулевого уравнения выражаем базисную переменную через небазисные и подставляем в предыдущие уравнения. Повторяя эту процедуру для всех базисных переменных, получаем фундаментальное решение.
Пример
Покажем, как методом Гаусса можно решить следующую систему:
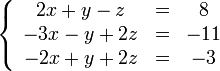
Обнулим
коэффициенты при
во
второй и третьей строчках. Для этого
вычтем из них первую строчку, умноженную
на
![]() и
и
![]() ,
соответственно:
,
соответственно:
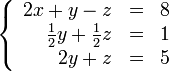
Теперь
обнулим коэффициент при
![]() в
третьей строке, вычтя из неё вторую
строку, умноженную на
в
третьей строке, вычтя из неё вторую
строку, умноженную на
![]() :
:
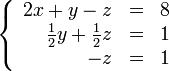
В результате мы привели исходную систему к треугольному виду, тем самым закончив первый этап алгоритма.
На втором этапе разрешим полученные уравнения в обратном порядке. Имеем:
![]() из
третьего;
из
третьего;
![]() из
второго, подставив полученное
из
второго, подставив полученное
![]()
![]() из
первого, подставив полученные
и
.
из
первого, подставив полученные
и
.
8 Вопрос
Под вектором
в элементарной математике понимают
направленный отрезок. Этот отрезок
изображается стрелкой и обозначается
или одной буквой со стрелкой (
![]() )
)
Операции над векторами
Сложение
Операцию сложения геометрических векторов можно определить несколькими в принципе эквивалентными способами, каждый их которых однако может быть удобнее или естественнее в зависимости от ситуации и типа рассматриваемых векторов. Так, правило треугольника наиболее простое и геометрически фундаментальное, удобно для сложения любого количества векторов, однако правило параллелограмма более удобно для фиксированных или скользящих векторов, т.к. не требует переноса второго слагаемого (что в принципе могло бы смущать или запутывать в этих случаях) для построения суммы, т.е. удобно для сложения векторов с началом в одной точке, в добавок имея то преимущество, что в нем более очевидно равноправие слагаемых; координатное же определение, являясь простым и удобным, бывает очень полезно для вычислений.
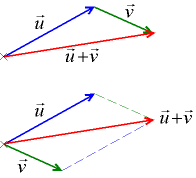
Два вектора u, v и вектор их суммы
Правило
треугольника.
Для сложения двух векторов
![]() и
и
![]() по
правилу треугольника
оба эти векторы переносятся параллельно
самим себе так, чтобы начало одного из
них совпадало с концом другого. Тогда
вектор суммы задаётся третьей стороной
образовавшегося треугольника, причём
его начало совпадает с началом первого
вектора, а конец с концом второго вектора.
Это правило прямо и естественно обобщается
для сложения любого количества векторов,
переходя в правило
ломаной:
начало второго вектор совмещается с
концом первого, начало третьего - с
концом второго итд, сумма же n
векторов есть вектор, с началом,
совпадающим с началом первого, и концом,
совпадающим с концом n-го
(т.е. изображается направленным отрезком,
замыкающим ломаную).
по
правилу треугольника
оба эти векторы переносятся параллельно
самим себе так, чтобы начало одного из
них совпадало с концом другого. Тогда
вектор суммы задаётся третьей стороной
образовавшегося треугольника, причём
его начало совпадает с началом первого
вектора, а конец с концом второго вектора.
Это правило прямо и естественно обобщается
для сложения любого количества векторов,
переходя в правило
ломаной:
начало второго вектор совмещается с
концом первого, начало третьего - с
концом второго итд, сумма же n
векторов есть вектор, с началом,
совпадающим с началом первого, и концом,
совпадающим с концом n-го
(т.е. изображается направленным отрезком,
замыкающим ломаную).
Правило параллелограмма. Для сложения двух векторов и по правилу параллелограмма оба эти векторы переносятся параллельно самим себе так, чтобы их начала совпадали. Тогда вектор суммы задаётся диагональю построенного на них параллелограмма, исходящей из их общего начала.
Сложение векторов с использованием координат. Каждая координата (см. Базис и разложение по базису) суммы векторов есть сумма соответствующей координаты всех (двух или более) суммируемых векторов. Например, для двумерного случая:
![]()
![]()
(Могут быть использованы прямоугольные или косоугольные координаты; правило сложения остаются одинаковыми для обоих этих типов координат).
Модуль (длину) вектора суммы
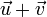 можно
вычислить, например, используя теорему
косинусов
можно
вычислить, например, используя теорему
косинусов
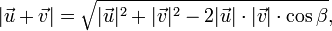 где
где
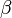 —
угол между отрезками, изображающими
данные векторы, когда начало одного
вектора совпадает с концом другого.
Или:
—
угол между отрезками, изображающими
данные векторы, когда начало одного
вектора совпадает с концом другого.
Или:
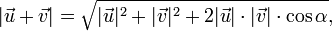 где
где
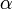 —
угол между векторами (выходящими из
одной точки).
—
угол между векторами (выходящими из
одной точки).
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.
Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.
Сложение коллинеарных скользящих векторов
Если
скользящие векторы параллельны, то при
их сложении главная трудность состоит
в определении прямой, на которой будет
расположена их сумма. (Величину и
направление вектора суммы было бы
естественно определить точно так же,
как и в случае сложения свободных
векторов.) В механике
при изучении статики
для решения вопроса о сложении параллельных
сил, которые, как известно, задаются
скользящими векторами, вводится
дополнительная гипотеза: к системе
векторов можно добавить два вектора,
равных по величине, противоположных по
направлению и расположенных на одной
прямой, пересекающей прямые, на которых
расположены данные векторы. Пусть,
например, надо сложить скользящие
векторы
![]() и
и
![]() ,
расположенные на параллельных прямых.
Добавим к ним векторы
,
расположенные на параллельных прямых.
Добавим к ним векторы
![]() и
и
![]() ,
расположенные на одной прямой. Прямые,
на которых расположены векторы
и
,
и
пересекаются.
Поэтому определены векторы
,
расположенные на одной прямой. Прямые,
на которых расположены векторы
и
,
и
пересекаются.
Поэтому определены векторы
![]()
Прямые,
на которых расположены векторы
![]() и
и
![]() ,
пересекаются всегда, за исключением
случая, когда векторы
и
равны
по величине и противоположны по
направлению, в котором говорят, что
векторы
и
,
пересекаются всегда, за исключением
случая, когда векторы
и
равны
по величине и противоположны по
направлению, в котором говорят, что
векторы
и
![]() образуют
пару
(векторов).
образуют
пару
(векторов).
Таким образом, под суммой векторов и можно понимать сумму векторов и , и эта сумма векторов определена корректно во всех случаях, когда векторы и не образуют пару.
Вычитание
Операция вычитания из вектора ветора сводится к сложению первого вектора и вектора, противоположного второму:
![]()
(Само сложение при этом осуществляется так, как описано в параграфе выше, пользуясь, если это удобно, любым из приведенных там альтернативных способов).
Однако
легко видеть, что из правила треугольника
можно получить и отдельное геометрическое
определение разности. Для этого достаточно
посмотреть на чертеж, иллюстрирующий
сложение по правилу треугольника и
осознать, что разность векторов
![]() и
на
этом чертеже есть вектор
и
на
этом чертеже есть вектор
![]() Отсюда
прямо формулируется правило
треугольника для вычитания векторов:
Отсюда
прямо формулируется правило
треугольника для вычитания векторов:
разность двух векторов с общим началом (или перенесенных параллельно так, чтобы начала совпали) есть вектор с началом, совпадающим с концом вычитаемого и концом, совпадающим с концом уменьшеаемого.
Это правило также может быть удобным.
Скалярное произведение
Основная статья: Скалярное произведение
![]()
Скалярное произведение двух векторов
Скалярное произведение на множестве геометрических векторов вводится, как
![]()
Скалярное
произведение любого вектора
и
какого-то единичного вектора
![]() есть
проекция
(ортогональная проекция) вектора
на
направление этого единичного вектора:
есть
проекция
(ортогональная проекция) вектора
на
направление этого единичного вектора:
![]()
Легко видеть, что скалярное произведение может быть записано через операцию (ортогонального) проецирования:
![]()
(где
![]() —
проекция вектора
на
направление
,
—
проекция вектора
на
направление
,
![]() —
проекция вектора
на
направление
).
—
проекция вектора
на
направление
).
В абстрактном подходе обычно сперва вводят скалярное произведение, а уже через него определяют понятие угла, ортогональность, ортогональную проекцию.
Векторное произведение
Основная статья: Векторное произведение
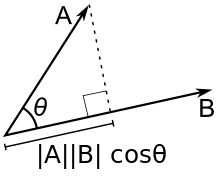
Векторное произведение двух векторов
Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:
длина вектора равна произведению длин векторов и на синус угла φ между ними
![]()
вектор ортогонален каждому из векторов и
вектор направлен так, что тройка векторов
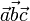 является
правой.
является
правой.
Обозначение:
![]()
Геометрически
векторное произведение
![]() есть
ориентированная площадь
параллелограмма,
построенного на векторах
есть
ориентированная площадь
параллелограмма,
построенного на векторах
![]() ,
представленная псевдовектором,
ортогональным этому параллелограмму.
,
представленная псевдовектором,
ортогональным этому параллелограмму.
Свойства векторного произведения:
При перестановке сомножителей векторное произведение меняет знак (антикоммутативность), т.е
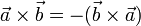
Векторное произведение обладает сочетательным свойством относительно скалярного множителя, то есть
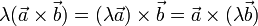
Векторное произведение обладает распределительным свойством:

