1.2. Электрическое поле в диэлектриках Основные определения

• Поляризованность и поток поляризованности через замкнутую поверхность :

, и , (1.2а)

где дипольные моменты молекул диэлектрика, алгебраическая сумма связанных зарядов внутри поверхности.

• Электрическое смещение и поток смещения через замкнутую поверхность:

, , (1.2б)

где алгебраическая сумма сторонних зарядов внутри поверхности.

• Дивергенция векторов и :

, , (1.2в)

где и объемная плотность связанных и сторонних зарядов соответственно.

• Условия на границе раздела двух диэлектриков:

, , , (1.2г)

где и поверхностные плотности связанных и сторонних зарядов на границе раздела, орт нормали направлен из первой среды во вторую, любое из касательных направлений.

• В случае изотропных диэлектриков:

, , (1.2д)

где диэлектрическая восприимчивость, а диэлектрическая проницаемость вещества.

• Напряженность поля точечного заряда , находящегося в жидкой изотропной среде:

. (1.2е)

1. В некоторой точке однородного изотропного диэлектрика проницаемостью известно значение модуля электрического смещения . Написать выражения для величин напряженности электрического поля и поляризованности в этой точке.

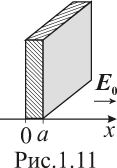2. П ластина толщиной , изготовленная из однородного диэлектрика проницаемостью , помещена в однородное электрическое поле величиной перпендикулярно силовым линиям, как показано на рис. 1.11. Определить: а) напряженность электрического поля в диэлектрике; б) плотность связанных зарядов на его левой поверхности. Изобразить качественно на графике зависимости , , и . Потенциал начала координат принять равным нулю. Пластину считать неограниченной в направлениях, перпендикулярных оси .

3. Точечный сторонний заряд расположен в центре сферического слоя, изготовленного из однородного диэлектрика проницаемостью . Внутренний радиус слоя , внешний . Построить примерные графики зависимостей , и , где расстояние от заряда . Определить плотность связанных зарядов на внутренней и на внешней поверхности диэлектрического слоя.

1. Сторонние заряды равномерно распределены с объемной плотностью по шару радиусом . Шар изготовлен из однородного изотропного диэлектрика проницаемостью . Определить: а) напряженность электрического поля как функцию расстояния от центра шара; б) объемную плотность связанных зарядов ; в) поверхностную плотность связанных зарядов .

2. Длинный цилиндрический стержень радиусом , изготовленный из однородного изотропного диэлектрика проницаемостью , равномерно заряжен сторонними зарядами с объемной плотностью . Определить: а) электрическое смещение ; б) напряженность электрического поля ; в) объемную плотность связанных зарядов в зависимости от расстояния от оси стержня.

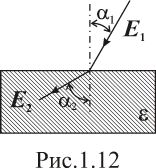
1. Вблизи плоской поверхности незаряженного однородного диэлектрика (рис.1.12) напряженность электрического поля в вакууме В/м. Углы и , определяющие направление силовых линий поля в вакууме и в диэлектрике, равны соответственно и . Найти: а) диэлектрическую проницаемость диэлектрика ; б) напряженность электрического поля в диэлектрике ; в) плотность связанных зарядов на его поверхности. Сторонних зарядов на границе раздела нет.

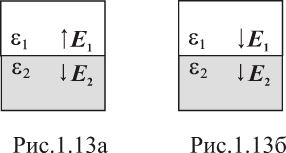
1. Сторонние заряды равномерно распределены по плоской границе раздела двух однородных диэлектриков, помещенных во внешнее поле; их поверхностная плотность Кл/м². Найти плотность связанных зарядов на этой границе, если известно, что в первой среде В/м, диэлектрическая проницаемость , , а поля и ориентированы, как показано на рис. 1.13а.

2. То же в варианте, изображенном на рис. 1.13б.

1. Диэлектрическую пластину толщиной поместили в однородное электрическое поле величиной перпендикулярно силовым линиям, как показано на рис. 1.11. Зависимость диэлектрической проницаемости материала от координаты имеет вид . Определить объемную плотность связанных зарядов в зависимости от .

1. Напряженность электрического поля в однородном диэлектрике проницаемостью зависит от координат как , где постоянная величина. Найти объемную плотность сторонних и связанных зарядов.

2. То же, если в пространстве, заполненном однородным диэлектриком проницаемостью , зависимость напряженности электрического поля от радиус-вектора имеет вид .

3. Чему будет равна поляризованность воды, если удастся выстроить ее молекулы так, чтобы все дипольные моменты оказались параллельными друг другу? Плотность воды кг/м³, молярная масса г/моль, дипольный момент одной молекулы Клּм.

4. В воде электрическое поле напряженностью В/м, создает поляризованность, эквивалентную правильной ориентации только одной из молекул. На основе этих данных вычислить диэлектрическую проницаемость воды . Для расчетов использовать данные, приведенные в предыдущей задаче.

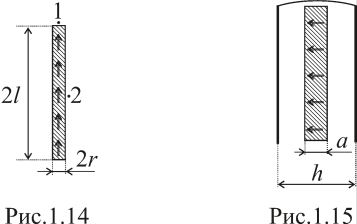1. Сегнетоэлектрический цилиндр длиной и радиусом обладает однородной остаточной поляризованностью , направленной вдоль оси цилиндра (рис.1.14). Найти напряженность электрического поля в точках 1 и 2, расположенных вблизи середины торца и середины боковой поверхности цилиндра.

5. Остаточная поляризованность круглого сегнетоэлектрического диска радиусом и толщиной повсюду в нем одинакова и вектор перпендикулярен оси диска. Найти напряженность электрического поля в центре диска, если .

6. Пластина из сегнетоэлектрика с остаточной поляризованностью помещена между металлическими обкладками, соединенными между собой проводником (рис.1.15). Вектор перпендикулярен боковым граням пластины. Определить векторы и внутри и вне сегнетоэлектрика. Толщина пластины , расстояние между обкладками . Краевыми эффектами пренебречь.