Списки: основные виды и способы реализации»

Целью работы является:

• изучение назначения и структуры динамических структур данных;

• освоение объявления и реализации динамических структур данных на примере списков;

• получение навыков работы со списками.

Задание на выполнение лабораторной работы

Разработать схему алгоритма и программу вычисления выражения в соответствии с вариантом задания.

Программа должна включать:

• объявление списка в соответствии с вариантом задания;

• ввод исходных данных и их обработка;

• вывод результатов выполнения программы.

Средства и оборудование

Персональная ЭВМ, среда программирования не ниже Borland Delphi 5.0.

Теоретические основы

К широко распространенным динамическим структурам данных относят такие структуры, как стек, очередь, одно- и двунаправленные списки, деки, деревья. Наиболее распространенными являются списки.

Список однонаправленный – структура данных, состоящая из односторонней последовательности элементов. Однонаправленный список можно представить в виде последовательности элементов данных с двумя указателями: на начальный и на текущий элементы. Каждый непоследний элемент в такой последовательности должен содержать указатель на следующий элемент, а последний элемент должен содержать либо неопределенный указатель, либо ссылку на первый элемент (в последнем случае получается циклический список). Элемент, на который ссылается текущий указатель, называется текущим (рис. 10).

Однонаправленный список должен реализовывать следующие операции:

• инициализация списка: присвоение текущему и начальному указателю неопределенного значения;

• помещение в список элемента: если текущий указатель определен, то указатель вставляемого (нового) элемента устанавливается равным указателю текущего элемента, указатель текущего элемента устанавливается на вставляемый элемент, после чего текущий указатель устанавливается на вставляемый элемент, в противном случае текущий и начальный указатели устанавливаются на новый элемент, указатель которого устанавливается неопределенным;

• получение значения текущего элемента;

• изменение значения текущего элемента;

• переход к следующему элементу;

• переход к начальному элементу;

• уничтожение списка.

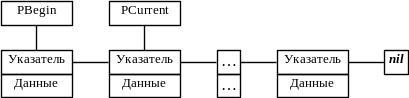
Рис. 10. Схематичная связь между элементами списка

Для организации списка необходимо объявить новый тип данных, отвечающий за отдельный элемент:

type

PElem = ^TElem; // указатель на элемент списка

TElem = record

Data: Extended; // данные текущего элемента

PNext: PElem; // указатель на следующий элемент

end;

При работе со списком требуются две дополнительные переменные

var

PBegin: PElem; // указатель на начало списка

PCurrent: PElem; // указатель на текущий элемент списка

Выделение памяти для нового элемента списка производится при помощи процедур

procedure New(var P: Pointer)

// или

procedure GetMem(var P: Pointer; Size: Integer).

Их отличие друг от друга в том, что процедура New выделяет память для типизированного указателя, а GetMem – для нетипизированного, например:

begin

New(PCurrent); // или

GetMem(PCurrent, sizeof(TElem));

…

end;

После завершения работы с динамическими данными необходимо удалить выделенную память, вызвав соответствующую процедуру

// удаление типизированного указателя

procedure Dispose(var P: Pointer);

// удаление нетипизированного указателя

procedure FreeMem(var P: Pointer[; Size: Integer]).

Обычно работа со списком производится в цикле, например, поиск некоторого значения будет выглядеть следующим образом:

PCurrent = PBegin;

while (PCurrent <> nil) do

begin

if (PCurrent^.Data > 10) then PCurrent^.Data = 10;

PCurrent = PCurrent^.PNext;

end;

Варианты заданий

1. Исходные данные – набор книг. Функции:

1. поиск книг, в названии которых существует заданная подстрока;

2. определение книг, выпущенных после заданного года.

2. Исходные данные – набор точек и радиус окружности на плоскости. Функции:

1. определение количества точек, принадлежащих окружности;

2. удаление из исходного набора точек, принадлежащих окружности.

3. Исходные данные – набор из 4–х точек на плоскости. Функции:

1. определение вида фигуры, которую определяет этот набор точек: ромб, квадрат и т.д.;

2. подсчет площади фигуры при условии, что фигура является квадратом или прямоугольником.

4. Исходные данные – информация в школьном журнале: фамилия, оценка. Функции:

1. определение количества и фамилий двоечников;

2. определение количества и фамилий учеников с баллом выше среднего по классу;

3. вставка и удаление заданных фамилий с перестроением списка.

5. Исходные данные – набор точек и координаты квадрата на плоскости. Функции:

1. определение количества точек, принадлежащих сторонам квадрата:

2. удаление из исходного набора точек, принадлежащих квадрату.

6. Исходные данные – набор точек на плоскости, определяющих треугольник. Функции:

1. определение является ли треугольник равнобедренным;

2. подсчет площади равнобедренного треугольника.

7. Исходные данные – набор четырехугольных фигур на плоскости. Функции:

1. определение типа фигуры: квадрат, прямоугольник и т.д.;

2. уменьшение прямоугольника до квадрата по минимальной стороне.

8. Исходные данные – набор треугольников на плоскости. Функции:

1. определение является ли фигура равносторонним треугольником;

2. вычисление площади равностороннего треугольника.

9. Исходные данные – набор прямых линий на плоскости. Функции:

1. определение являются ли все прямые, параллельными заданной прямой;

2. изменение параметров прямой, чтобы она была параллельна горизонтальной оси.

10. Исходные данные: набор точек и прямая линия на плоскости. Функции:

1. определение количества точек, принадлежащих прямой линии объекта;

2. изменение угла наклона прямой на заданную величину.

11. Многочлен 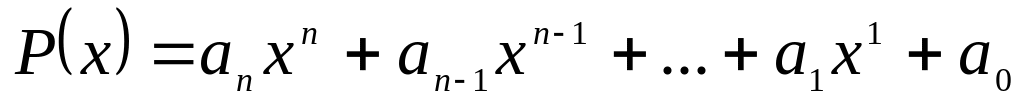с целыми коэффициентами представить в виде списка. Если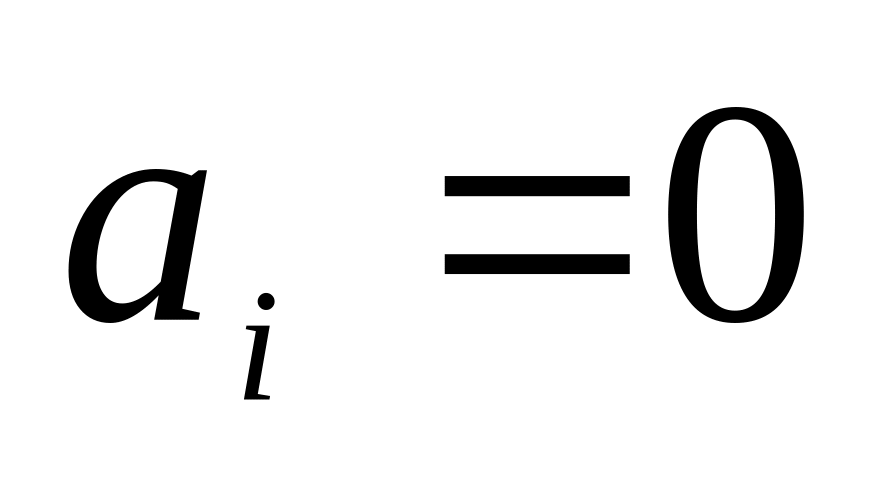 , то соответствующее звено не включается в список. Описать тип данных, соответствующий такому представлению многочленов, и определить следующие функции и процедуры для работы с этими списками-многочленами:

1. логическую функцию, проверяющую равенство многочленов;

2. функцию, вычисляющую значение многочлена в целочисленной точке;

3. процедуру, которая строит производную многочлена;

4. процедуру, которая строит сумму двух многочленов.

Контрольные вопросы

1. Назовите основные динамические структуры данных.

2. Расскажите о структуре однонаправленного списка.

3. Приведите схематический рисунок расположения элементов списка в памяти.

4. Назовите основные операции однонаправленного списка.

Лабораторная работа №18

Тема: «Программирование рекурсивных алгоритмов»

Целью работы является:

• изучение назначения рекурсивных алгоритмов;

• освоение объявления и реализации рекурсивных процедур и функций;

• получение навыков работы с рекурсивными алгоритмами.

Задание на выполнение лабораторной работы

Разработать схему алгоритма и программу вычисления выражения в соответствии с вариантом задания.

Программа должна включать:

• объявление рекурсивной процедуры в соответствии с вариантом задания;

• ввод исходных данных и их обработка;

• вывод результатов выполнения программы.

Средства и оборудование

Персональная ЭВМ, среда программирования не ниже Borland Delphi 5.0.

Теоретические основы

Рекурсия – есть метод определения множества объектов или процесса в терминах самого себя. Любое рекурсивное определение содержит две части: базисную часть и рекурсивную.

Рекурсивный алгоритм реализует какое-либо рекурсивное определение посредством разбиения решаемой задачи на подзадачи меньшей размерности, выполняемые с помощью одного и того же алгоритма. Процесс разбиения завершается при достижении простейших возможных решаемых задач, которые называются условиями завершения. Таким образом, рекурсивное определение алгоритма включает две части:

• условия завершения (одно или несколько), которые могут быть вычислены для определенных параметров. Условия завершения соответствуют базисной части рекурсивного определения;

• шаг рекурсии, в котором текущие значения некоторых переменных в алгоритме могут быть определены в терминах их предыдущих значений. В конечном итоге шаг рекурсии должен приводить к выполнению условий завершения.

Рекурсивные алгоритмы реализуются через рекурсивные процедуры (функции). Рекурсивной называется процедура, которая в процессе выполнения явно или неявно вызывает сама себя. Прямая (явная) рекурсия характеризуется наличием в теле процедуры оператора обращения к ней же самой. В случае косвенной (неявной) рекурсии одна процедура обращается к другой, которая (возможно через цепочку вызовов других процедур) вновь обращается к первой.

Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.

Следует сказать, что время работы рекурсивного алгоритма по сравнению с итеративным будет больше, поскольку при передаче параметров через стек потребуются дополнительные затраты времени.

В основе рекурсивного вычислительного процесса лежит рекурсивный цикл, который реализуется через вызов рекурсивной процедуры.

Общая схема рекурсивного цикла:

procedure RecursExample (…);

begin

if < условие рекурсивного цикла > then

begin

< тело рекурсивного цикла; >

RecursExample (…);

end;

end;

Следует избегать избыточной глубины рекурсии, так как это может вызвать переполнение стека.

Варианты заданий

1. Найти рекурсивную формулу для возведения числа в целую степень.

2. Найти рекурсивную формулу и вычислить факториал указанного числа.

3. Если какое либо число 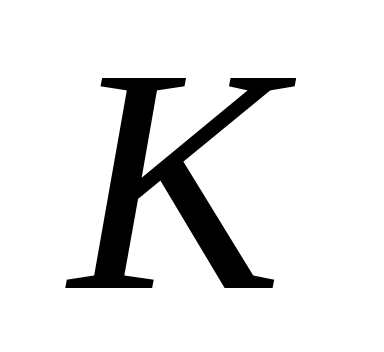является нечетным целым числом, то нечетными целыми будут числа, определяемые выражениям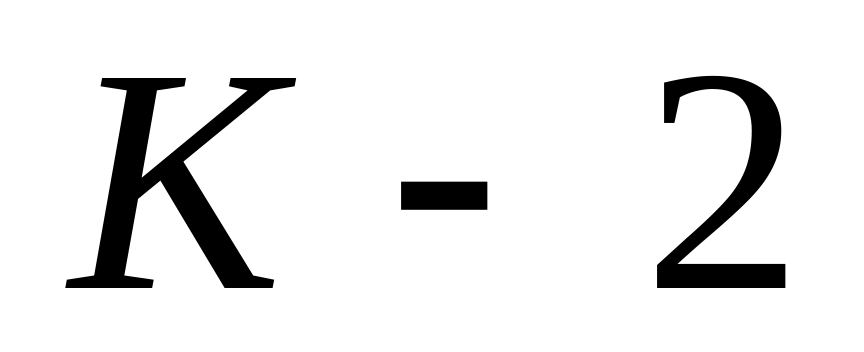и и 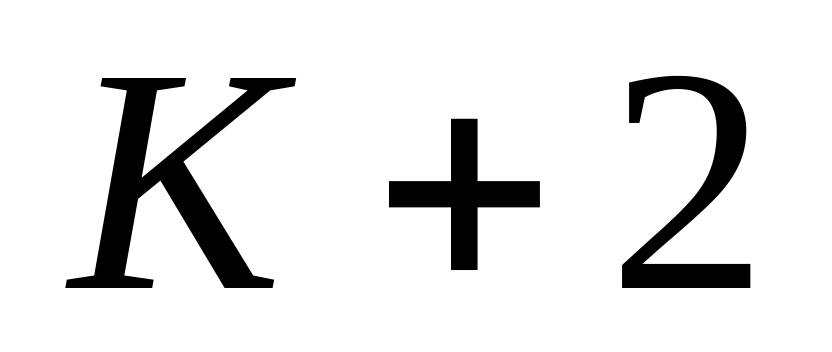. При помощи рекурсии доказать, что указанное число K является нечетным целым числом.

4. Вычислить выражение, используя рекурсию

5. Написать программу, включающую рекурсивную функцию для вычисления:

   1. наибольшего общего делителя (НОД) двух неотрицательных целых чисел 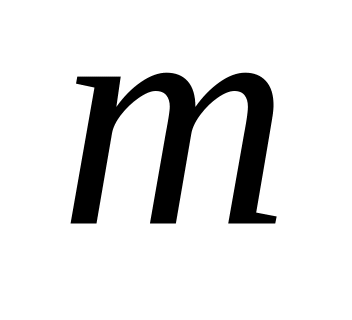и 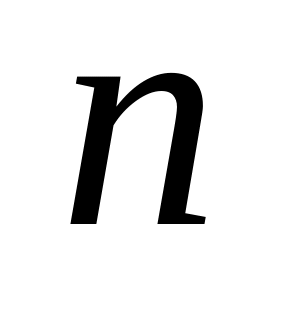с использованием алгоритма Евклида

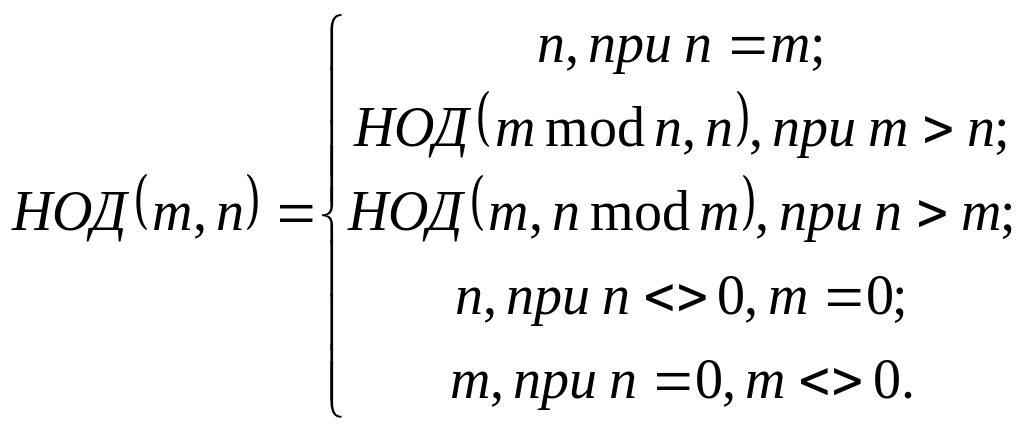
2. НОД двух неотрицательных целых чисел и с использованием первого алгоритма Евклида

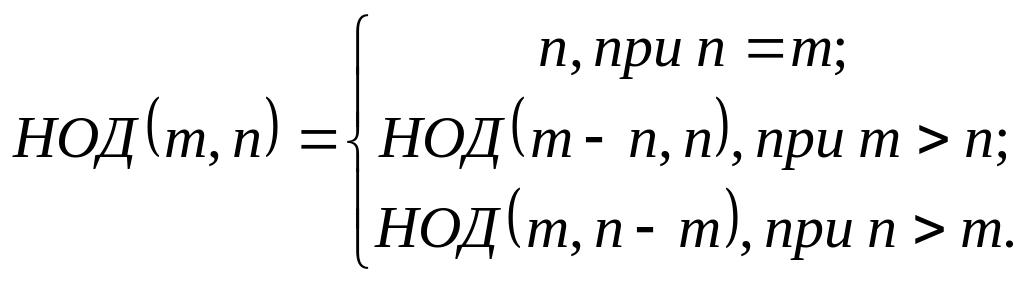
3. биноминального коэффициента 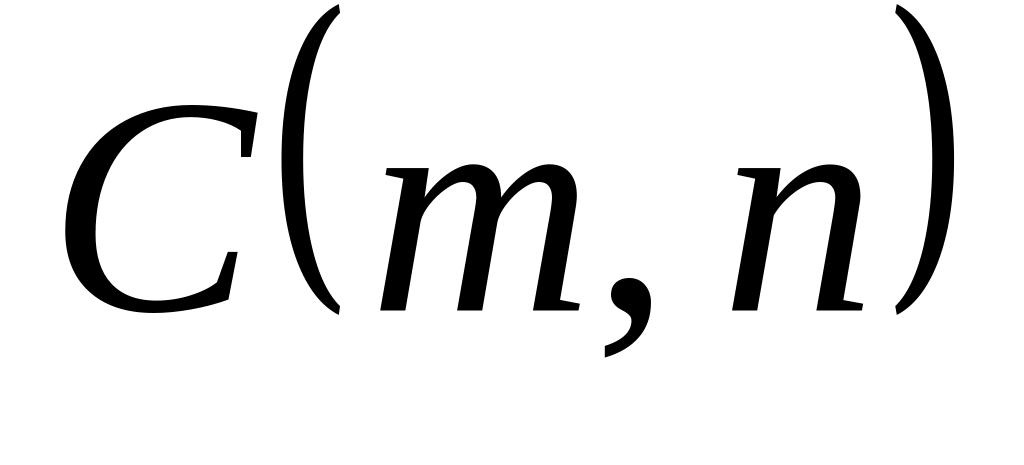, где 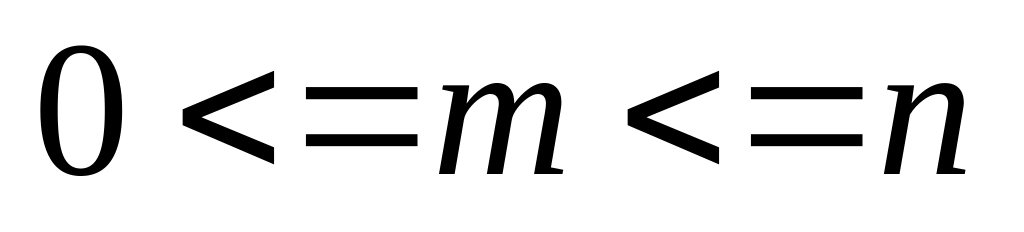формуле

4. величины 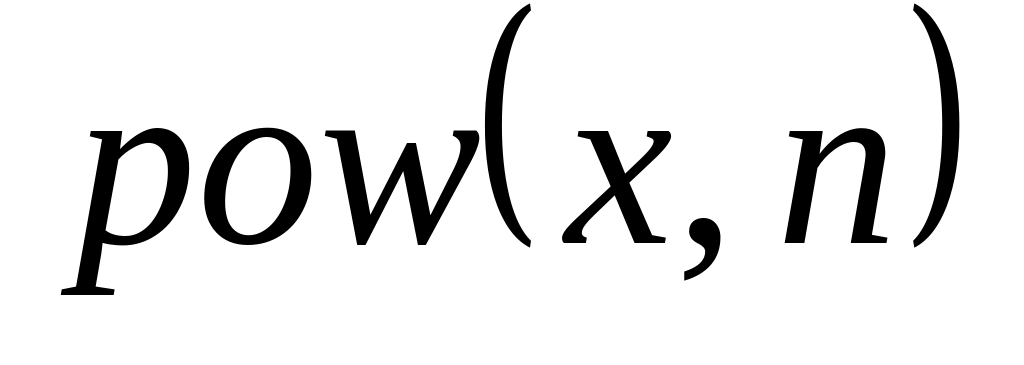для вещественного и целого по формуле

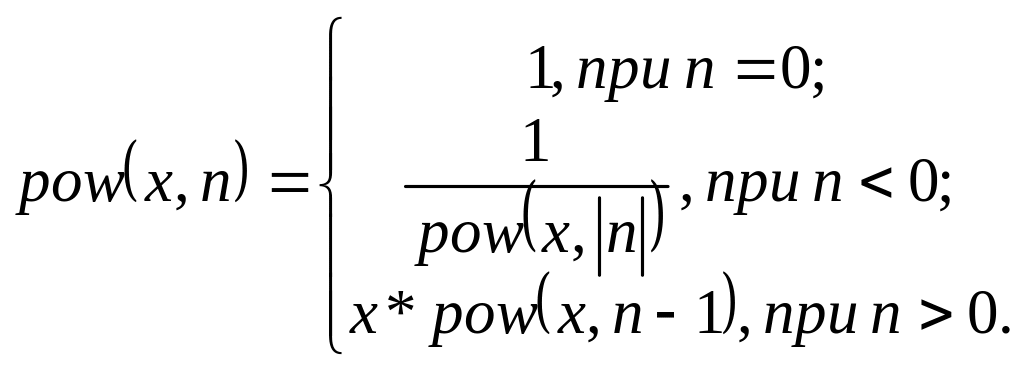
5. функции Аккермана 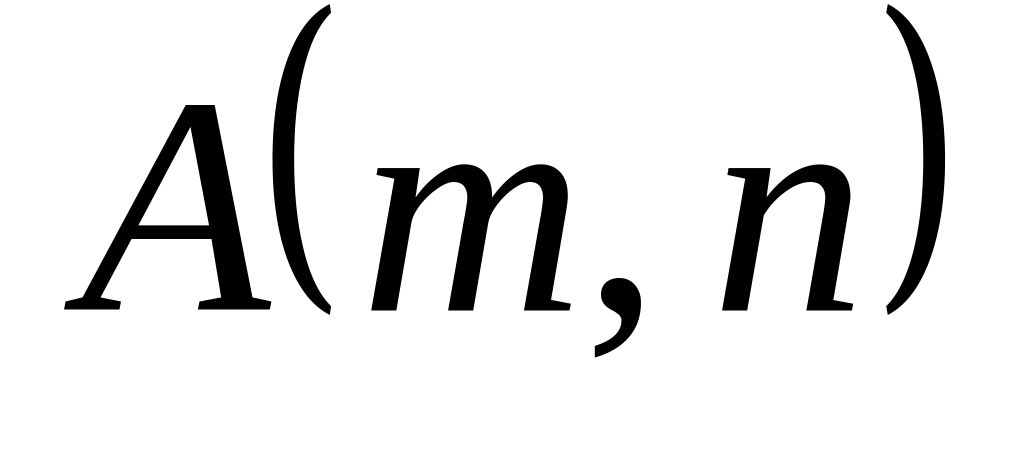для неотрицательных целых чисел и по формуле

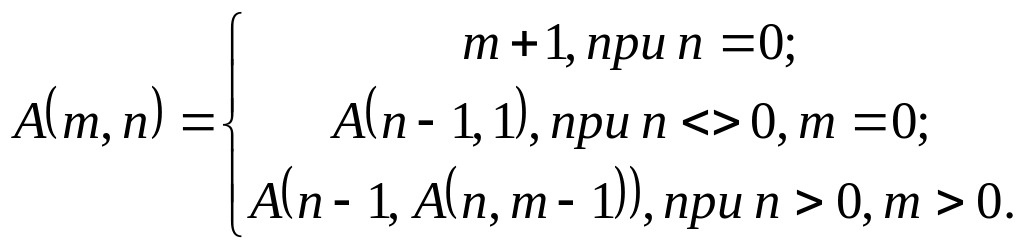
6. числа Каталана 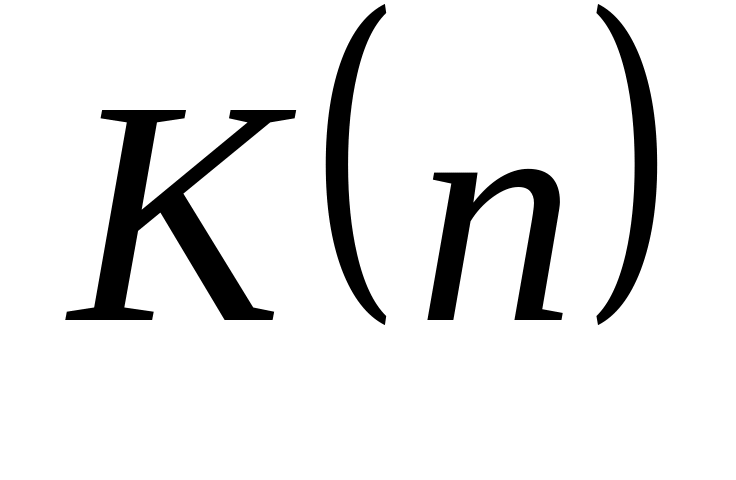для натурального по формуле

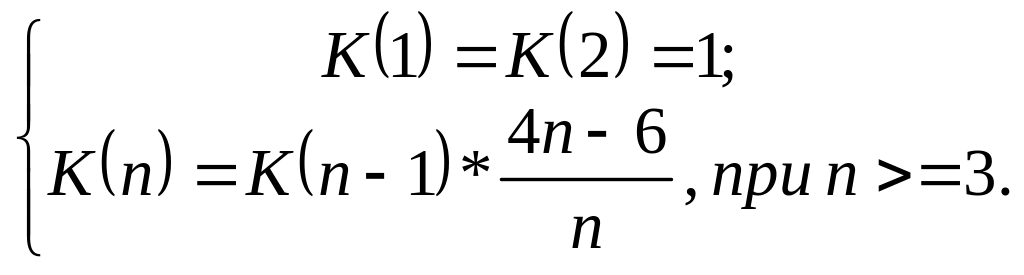
7. функции 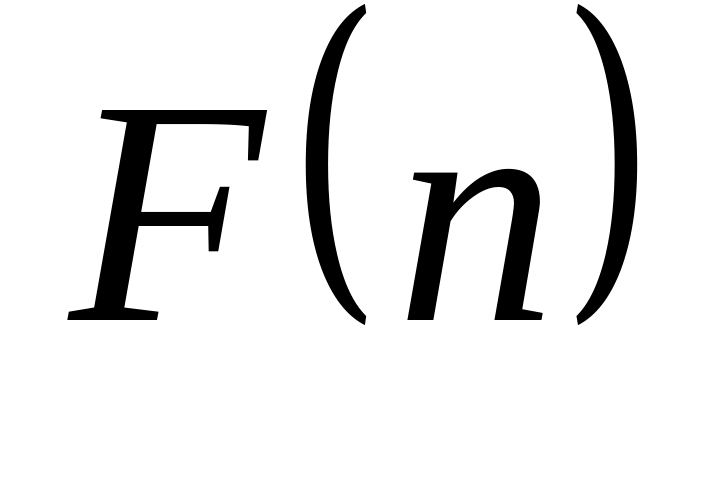для целого положительного по формуле

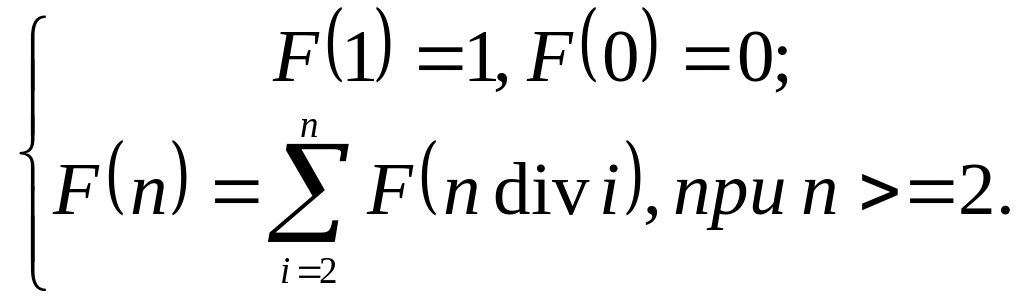
6. Определить функцию , которая возвращает количество цифр в заданном натуральном числе n:

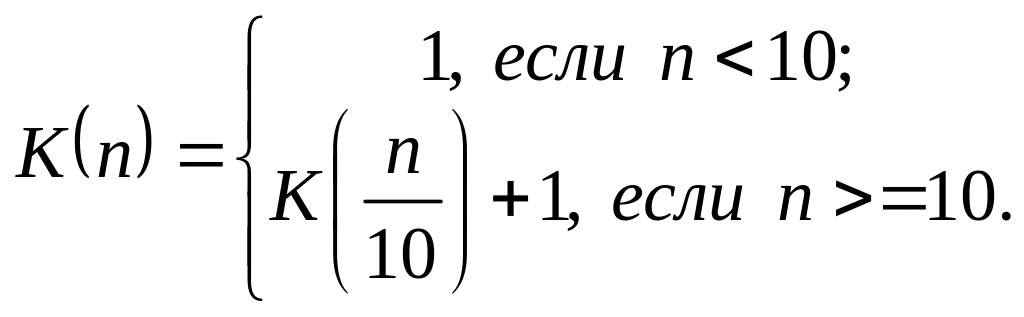
7. По аналогии с предыдущим заданием определите функцию 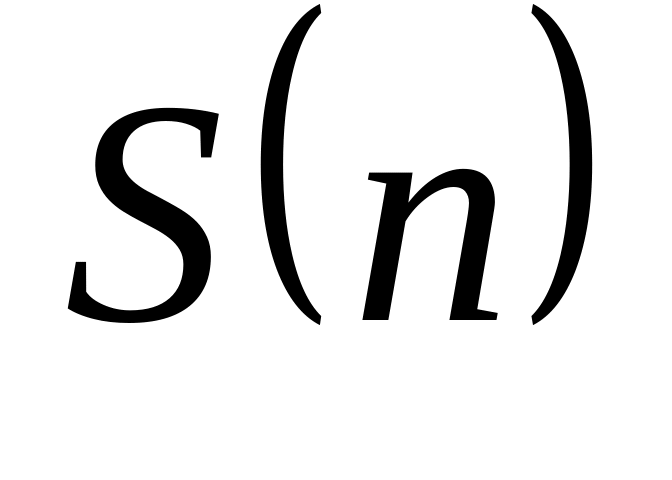, вычисляющую сумму цифр заданного натурального числа.

8. Определить функцию , где , для вычисления биномиального коэффициента 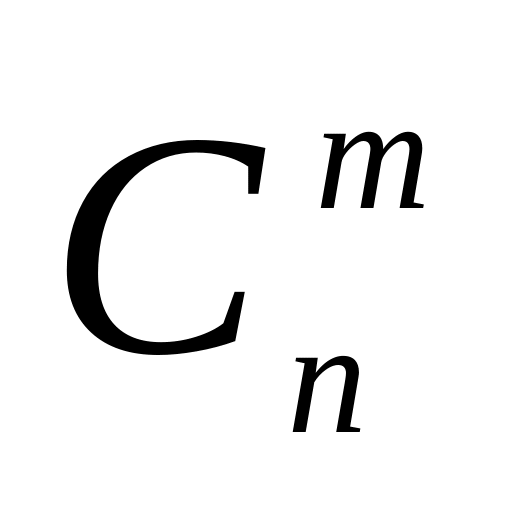по следующей формуле

.

9. Числа Фибоначчи 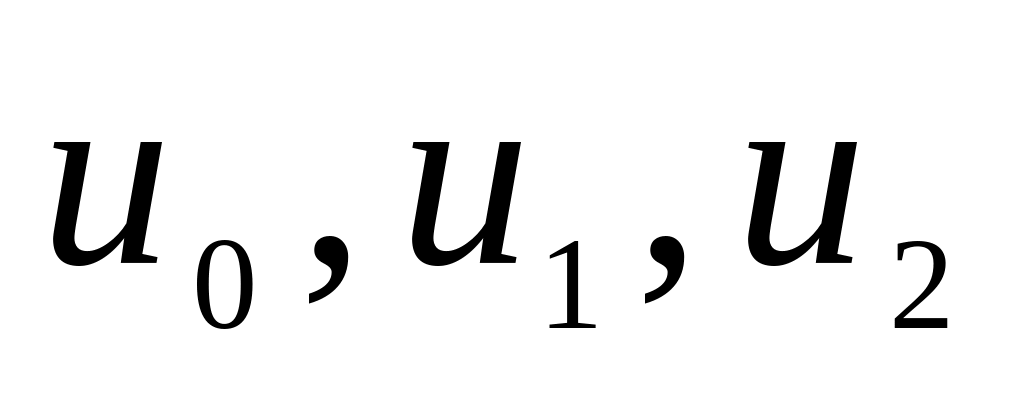определяются следующим образом:

1. написать программу вычисления первого числа Фибоначчи, большего m ( ).

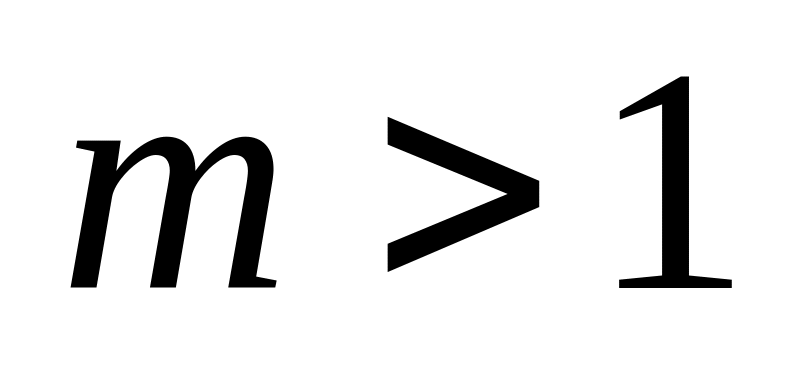2. написать программу вычисления 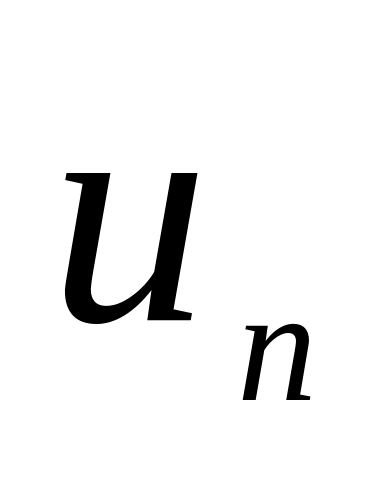для данного неотрицательного целого n.

1. Палиндром – сочетания символов, которые читаются одинаково туда и обратно (например, числа 4884, 121). Написать программу-палиндром для первых 100 чисел. Начать с любого положительного числа. Если это не палиндром, реверсируем его цифры и складываем исходное число с числом, полученным в результате реверсирования. Если сумма не палиндром, то повторить действия и выполнять их до тех пор, пока не будет получен палиндром (рис. 2).

+	78
	87
+	165
	561
+	726
	627
+	1353
	3531
	4884

Рис. 11. Поиск палиндрома

11. Разбиения. Целое число можно представить как сумму его частей, называемых разбиениями. Так, число 4 можно представить как: 4; 3+1; 2+2; 2+1+1; 1+1+1+1. Составить программу, которая читает число и печатает разбиения числа и количество разбиений 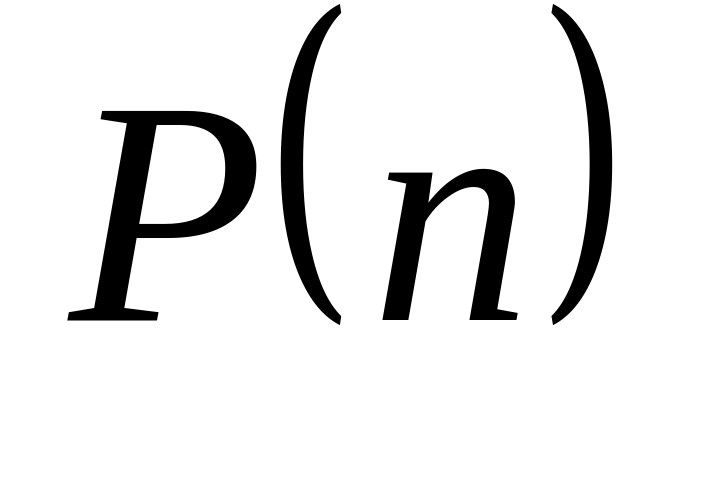(например ).

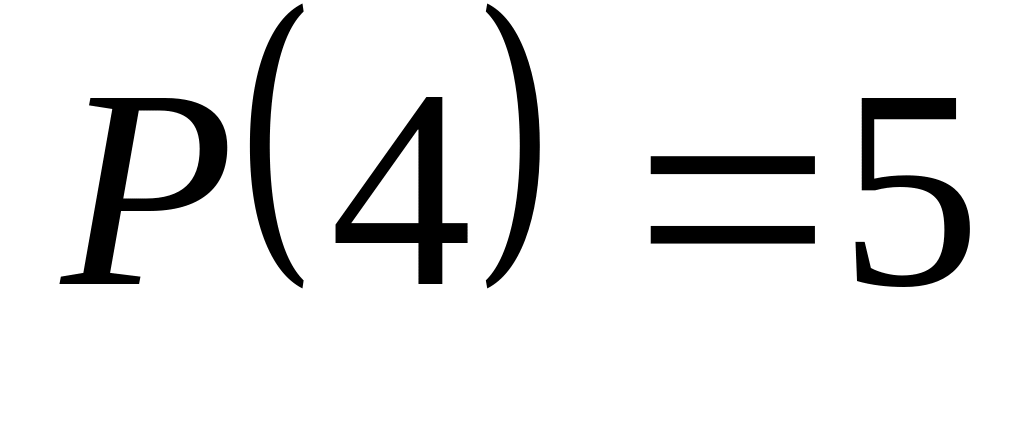12. Дано произвольное бинарное дерево (дерево, имеющее не более двух потомков). Написать функцию, определяющую его высоту, т.е. максимальную длину пути от вершины-корня к листу. Написать функцию, выводящую информационные поля лишь тех узлов дерева, которые расположены на уровнях иерархии больших или равных числу N (уровни иерархии увеличиваются от вершины корня к листьям). Оформить бинарное дерево в виде класса.

13. При помощи рекурсии реализовать задачу о “ханойских башнях”, состоящую в следующем. Есть три стержня, на первый из которых надета пирамидка из N колец (большие кольца снизу, меньшие сверху). Требуется переместить кольца на другой стержень. Разрешается перекладывать кольца со стержня на стержень, но класть большее кольцо поверх меньшего нельзя.

14. В указанной директории и поддиректориях:

1. найти файлы, содержащие в имени какую-либо подстроку;

2. найти файлы с расширением *.exe;

3. показать структуру каталогов;

4. найти все файлы с атрибутом только для чтения;

5. найти все скрытые файлы и директории;

6. найти все системные файлы;

7. показать все файлы (не директории), исключая файлы с атрибутами: архивные, только для чтения, скрытые, системные. Не искать файлы в скрытых и системных директориях;

8. найти все файлы и директории и указать их атрибуты;

9. отобразить все файлы, созданные после указанной даты;

10. отобразить все файлы, измененные в ночное время.

Контрольные вопросы

1. Что такое рекурсия, из каких частей она состоит.

2. Что такое граничное условие, каково его назначение в рекурсивной подпрограмме.

3. Дайте понятие прямой, косвенной рекурсии.

4. Приведите пример рекурсии.

5. Что такое глубина рекурсии.

Литература

1. Йенсен К., Вирт Н. Паскаль: руководство пользователя. – М.: Финансы и статистика, 1989 г. – 255 с.

2. Архангельский А.Я. Delphi 7. Справочное пособие – М.: «Бином-Пресс», 2004 г. – 1024 с.

3. Голицина О.Л., Максимов Н.В., Попов И.И. Базы данных – М.: «ИНФРА-М», 2004. – 352 с.

4. Вирт Н. Алгоритмы и структуры данных. – М.: Мир, 1989 г. – 352 с. 

5. Буч Г. Объектно-ориентированное проектирование с примерами применения: пер. с англ. – М.: Конкорд. – 1992 г.

6. Страуструп Б. Язык программирования С++. – СПб.: «Бином. Лаборатория знаний», 2000 г. – 816 с.

Содержание отчета по лабораторным работам

1. Постановка задачи:

1. текст задания;

2. допущения и ограничения;

3. определение входной информации, необходимой для решения задачи;

4. определение выходной информации, являющейся результатом работы;

5. алгоритм решения задачи.

2. Описание программы.

   1. Общие сведения:

1. наименование программы;

2. требования к аппаратному и программному обеспечению;

3. типы устройств, используемых в программе;

4. условные обозначения.

1. Структура программы:

1. структура данных;

2. организация пользовательского интерфейса;

3. сведения о функциональных ограничениях;

4. описание составных частей программы и их взаимосвязи;

5. блок-схема программы (составных частей программы).

3. Заключение:

1. анализ алгоритма решения задачи;

2. анализ структуры программы;

3. анализ полученных результатов (полнота, достоверность).

4. Приложение:

1. текст программы с подробными комментариями;

2. таблицы вспомогательных цифровых данных;

3. иллюстрации вспомогательного характера.

Горохов Максим Михайлович

Корепанов Андрей Владимирович

ПРАКТИКУМ ПО ПРОГРАММИРОВАНИЮ НА ЯЗЫКЕ PASCAL

учебное пособие для студентов направления