12. Объёмная плотность энергии электрического поля. Энергия электрического поля и работа поляризации диэлектрика.

Объёмная плотность энергии эл поля- это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля объемная плотность энергии равна   . Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем

С учетом, что   и 

Энергия электрического поля. Энергию заряженного конденсатора можно выразить через величины, характеризующие электрическое поле в зазоре между обкладками. Сделаем это на примере плоского конденсатора. Подстановка выражения для емкости в формулу для энергии конденсатора дает

Частное U / d равно напряженности поля в зазоре; произведение S·d представляет собой объем V, занимаемый полем. Следовательно,  Если поле однородно (что имеет место в плоском конденсаторе при расстоянии  d много меньшем, чем линейные размеры обкладок), то заключенная в нем энергия распределяется в пространстве с постоянной плотностью w. Тогда объемная плотность энергии электрического поля равна 

C учетом соотношения  можно записать 

В изотропном диэлектрике направления векторов D и E совпадают и  Подставим выражение  , получим 

Первое слагаемое в этом выражении совпадает с плотностью энергии поля в вакууме. Второе слагаемое представляет собой энергию, затрачиваемую на поляризацию диэлектрика. Покажем это на примере неполярного диэлектрика. Поляризация неполярного диэлектрика заключается в том, что заряды, входящие в состав молекул, смещаются из своих положений под действием электрического поляЕ. В расчете на единицу объема диэлектрика работа, затрачиваемая на смещение зарядов q_i на величину dr_i, составляет 

Выражение в скобках есть дипольный момент единицы объема или поляризованность диэлектрика Р. Следовательно,  . Вектор P связан с вектором E соотношением  . Подставив это выражение в формулу для работы, получим

Проведя интегрирование, определим работу, затрачиваемую на поляризацию единицы объема диэлектрика .

Зная плотность энергии поля в каждой точке, можно найти энергию поля, заключенного в любом объеме V. Для этого нужно вычислить интеграл:

13. Ток проводимости. Условия возникновения тока проводимости. Сила и плотность тока.

  Током проводимости называют упорядоченное движение в веществе или вакууме свободных заряженных частиц – электронов проводимости (в металлах), положительных и отрицательных ионов (в электролитах), электронов и положительных ионов (в газах), электронов проводимости и дырок (в полупроводниках), пучков электронов (в вакууме). 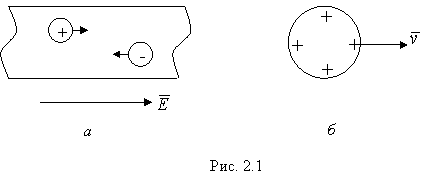Этот ток обусловлен тем, что в проводнике под действием приложенного электрического поля напряженностью   происходит перемещение свободных электрических зарядов (рис. 2.1, а). 

Для возникновения и поддержания электрического тока проводимости необходимы следующие условия:       1) наличие свободных носителей тока (свободных зарядов);       2) наличие электрического поля, создающего упорядоченное движение свободных зарядов;       3) на свободные заряды, помимо кулоновских сил, должны действовать сторонние силы неэлектрической природы; эти силы создаются различными источниками тока (гальваническими элементами, аккумуляторами, электрическими генераторами и др.);       4) цепь электрического тока должна быть замкнутой. 

Количественной мерой электрического тока является сила тока I - скалярная физическая величина, определяемая электрическим зарядом, проходящим через поперечное сечение S проводника в единицу времени:      

   

Единица силы тока – ампер (А).

Плотностью тока   называют векторную физическую величину, совпадающую с направлением тока в рассматриваемой точке и численно равную отношению силы тока dI, проходящего через элементарную поверхность, перпендикулярной направлению тока, к площади этой поверхности:        

     

      Единица плотности тока – ампер на квадратный метр (А/м^2).