9. Напряжённость и индукция электрического поля на границе раздела двух сред. Преломление линии электрического поля.

Р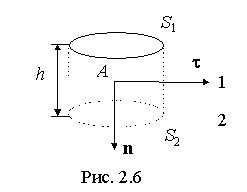 ассмотрим поведение векторов E и D на границе раздела двух однородных изотропных диэлектриков с проницаемостями   и   при отсутствии на границе свободных зарядов. Граничные условия для нормальных составляющих векторов D и E следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к границе раздела, а основания находятся на равном расстоянии от границы (рис. 2.6).

Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность .Выделяя потоки через основания и боковую поверхность цилиндра ,

г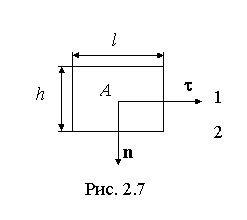 де   - значение   касательной составляющей усредненное по боковой поверхности  . Переходя к пределу при  (при   этом также стремится к нулю), получаем  , или окончательно для нормальных составляющих вектора электрической индукции . Для нормальных составляющих вектора напряженности поля получим . Таким образом, при переходе через границу раздела диэлектрических сред нормальная составляющая вектора   терпит разрыв, а нормальная составляющая вектора   непрерывна. Граничные условия для касательных составляющих векторов D и E следуют из соотношения, описывающего циркуляцию вектора напряженности электрического поля. Построим вблизи границы раздела прямоугольный замкнутый контур длины l и высоты h (рис. 2.7). 

, представим циркуляцию вектора E в следующем виде: , где   - среднее значение E_n на боковых сторонах прямоугольника. Переходя к пределу при  , получим для касательных составляющих E

Для касательных составляющих вектора электрической индукции граничное условие имеет вид

Т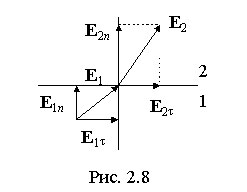 аким образом, при переходе через границу раздела диэлектрических сред касательная составляющая вектора   непрерывна, а касательная составляющая вектора   терпит разрыв. Преломление линий электрического поля. Из граничных условий для соответствующих составляющих векторов E и D следует, что при переходе через границу раздела двух диэлектрических сред линии этих векторов преломляются (рис. 2.8). Разложим векторы E₁ и E₂ у границы раздела на нормальные и тангенциальные составляющие и определим связь между углами   и   при условии  . Легко видеть, что как для напряженности поля, так и для индукции справедлив один и тот же закон преломления линий напряженности и линий смещения 

При переходе в среду с меньшим значением   угол, образуемый линиями напряженности (смещения) с нормалью, уменьшается, следовательно, линии располагаются реже. При переходе в среду с большей линии векторов E и D, напротив, сгущаются и удаляются от нормали.

10. Распределение зарядов на проводящих телах. Электрическое поле вблизи поверхности заряженного проводника. Потенциал и энергия заряженного проводящего тела.

Все вещества в соответствии с их способностью проводить электрический ток подразделяются на проводники, диэлектрики и полупроводники. Проводниками называют вещества, в которых электрически заряженные частицы - носители заряда - способны свободно перемещаться по всему объему вещества. К проводникам относятся металлы, растворы солей, кислот и щелочей, расплавленные соли, ионизированные газы.

Ограничим рассмотрение твердыми металлическими проводниками, имеющими кристаллическую структуру. Эксперименты показывают, что при очень малой разности потенциалов, приложенной к проводнику, содержащиеся в нем электроны проводимости, приходят в движение и перемещаются по объему металлов практически свободно.

В отсутствие внешнего электростатического поля электрические поля положительных ионов и электронов проводимости взаимно скомпенсированы, так что напряженность внутреннего результирующего поля равна нулю.

При внесении металлического проводника во внешнее электростатическое поле с напряженностью Е₀ на ионы и свободные электроны начинают действовать кулоновские силы, направленные в противоположные стороны. Эти силы вызывают смещение заряженных частиц внутри металла, причем в основном смещаются свободные электроны, а положительные ионы, находящиеся в узлах кристаллической решетки, практически не меняют своего положения. В результате внутри проводника возникает электрическое поле с напряженностью Е^'.

Смещение заряженных частиц внутри проводника прекращается тогда, когда суммарная напряженность поля Е в проводнике, равная сумме напряженностей внешнего и внутреннего полей, станет равной нулю: Представим выражение, связывающее напряженность и потенциал электростатического поля, в следующем виде: где Е - напряженность результирующего поля внутри проводника; n - внутренняя нормаль к поверхности проводника. Из равенства нулю результирующей напряженности Е следует, что в пределах объема проводника потенциал имеет одно и то же значение:  .

Полученные результаты позволяют сделать три важных вывода:

1. Во всех точках внутри проводника напряженность поля  , т. е. весь объем проводника эквипотенциален.

2. При статическом распределении зарядов по проводнику вектор напряженности Ена его поверхности должен быть направлен по нормали к поверхности  , в противном случае под действием касательной к поверхности проводника компоненты напряженности   заряды должны перемещаться по проводнику.

3. Поверхность проводника также эквипотенциальна, так как для любой точки поверхности

 

(+лекция)