
- •Электрический заряд и его свойства. Электрическое поле. Напряженность и индукция электрического поля. Закон Кулона. Теорема Гауса.
- •Напряженность электрического поля точечного заряда. Принцип суперпозиции. Примеры расчета электрического поля распределенных зарядов.
- •3) Применение теоремы Гаусса для расчета электрического поля заряженных тел
- •Потенциал электростатического поля. Циркуляция напряженности электрического поля. Работа перемещения заряда в электрическом поле. Энергия системы электрических зарядов.
- •Уравнение Пуассона
- •Примеры расчёта потенциала электрического поля для распределённых зарядов.
- •Электрический диполь. Поле электрического диполя. Силы, действующие на диполь в электрическом поле. Энергия электрического диполя в электрическом поле.
- •Диэлектрики в электрическом поле. Связанные заряды. Поляризованность. Диэлектрическая проницаемость и восприимчивость. Электрическое смещение.
- •9. Напряжённость и индукция электрического поля на границе раздела двух сред. Преломление линии электрического поля.
- •10. Распределение зарядов на проводящих телах. Электрическое поле вблизи поверхности заряженного проводника. Потенциал и энергия заряженного проводящего тела.
- •11. Электроёмкость. Конденсаторы. Примеры расчёта ёмкости конденсатора.
- •12. Объёмная плотность энергии электрического поля. Энергия электрического поля и работа поляризации диэлектрика.
- •13. Ток проводимости. Условия возникновения тока проводимости. Сила и плотность тока.
- •14. Уравнение непрерывности.
- •15. Сторонние силы. Электродвижущая сила. Электрическая цепь. Закон Ома и Джоуля-Ленца. Однородный и неоднородный участок цепи. Разность потенциалов и падение напряжения.
3) Применение теоремы Гаусса для расчета электрического поля заряженных тел
а) Поле равномерно заряженной плоскости.
 Электрическое
поле, создаваемое бесконечно протяженной
равномерно заряженной плоскостью,
является однородным – в каждой точке
пространства вне плоскости его
напряженность всюду одинакова. Направлено
это поле перпендикулярно к плоскости
в обе стороны (рис.2.5). Поэтому для потока
вектора напряженности поля через
произвольно выбранную цилиндрическую
поверхность, опирающуюся на элемент
плоскости ΔS, можем написать:
Электрическое
поле, создаваемое бесконечно протяженной
равномерно заряженной плоскостью,
является однородным – в каждой точке
пространства вне плоскости его
напряженность всюду одинакова. Направлено
это поле перпендикулярно к плоскости
в обе стороны (рис.2.5). Поэтому для потока
вектора напряженности поля через
произвольно выбранную цилиндрическую
поверхность, опирающуюся на элемент
плоскости ΔS, можем написать:
![]() ,
откуда
,
откуда
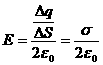 ,
где
,
где![]() - поверхностная плотность заряда.
Размерность
в СИ:
- поверхностная плотность заряда.
Размерность
в СИ:
![]() .
.
Рис.2.5. Поле равномерно заряженной плоскости.
Таким
образом, искомая напряженность
электрического поля равномерно
заряженной
плоскости
![]() .
.
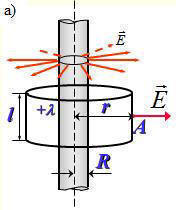
б) Поле равномерно заряженного бесконечного цилиндра (нити)
Рис. 1.13. Электрическое поле равномерно заряженного цилиндра |
Бесконечный цилиндр радиуса R заряжен равномерно; линейная плотность заряда равна l. Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный с заряженным цилиндр радиуса r и высотой l (рис. 1.13 а). Поскольку вектор напряженности параллелен торцам, поток сквозь основания цилиндра равен нулю, и
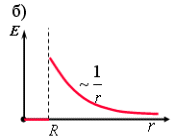
Отсюда при r R
Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области Е = 0. График зависимости E от r приведен на рис. 1.13 б.
|
в) Поле объемно заряженного шара.
Ш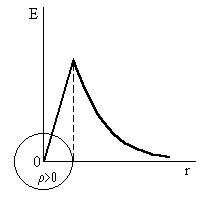 ар
радиуса R
с общим зарядом Q
равномерно заряжен с объемной плотностью
+ρ
ар
радиуса R
с общим зарядом Q
равномерно заряжен с объемной плотностью
+ρ
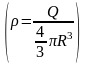 .
Поле обладает сферической симметрией
и потому силовые линии направлены
радиально.
.
Поле обладает сферической симметрией
и потому силовые линии направлены
радиально.
Проведем мысленно сферу, радиуса r с центром, совпадающим с центром заряженного шара.
При r>R внутрь поверхности попадает весь заряд Q. По теореме Остроградского-Гаусса
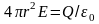 →
→ 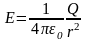
При
r<R внутри мысленной поверхности
содержится заряд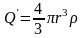
Тогда, по теореме Остроградского-Гаусса
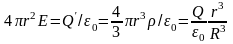 →
→ 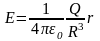
Таким образом, внутри равномерно заряженного шара напряженность поля изменяется линейно.
г) Диэлектрический шар.
Р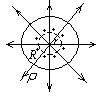
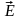
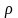 (рис.2.8).
(рис.2.8).
Размерность
объемной плотности заряда в СИ:
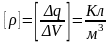 .
.
Рис.2.8. Поле равномерно заряженного диэлектрического шара.
Полный
заряд шара, очевидно, есть:
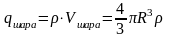 .
.
Имеем по теореме Гаусса:
1)
Внутри
шара
(r
< R):
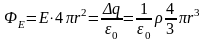 , где Δq
=
, где Δq
=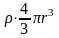 - заряд внутренней области шара,
ограниченной выбранной сферической
поверхностью радиуса r.
Отсюда находим:
- заряд внутренней области шара,
ограниченной выбранной сферической
поверхностью радиуса r.
Отсюда находим:
 .
.
2)
Вне
шара
(r
> R):
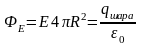 ,
откуда
,
откуда
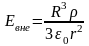 =
=
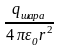 ,
,
то есть вне заряженного диэлектрического шара электрическое поле такое же, как и в случае металлического шара.
На рис.2.9 показан качественный ход зависимостей E(r) для металлического и диэлектрического шаров.
металл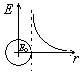 Рис.2.9.
Зависимость E(r).
Рис.2.9.
Зависимость E(r).
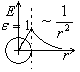 диэлектрик
диэлектрик

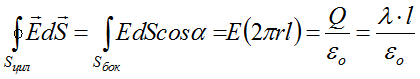 .
.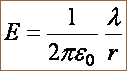 .
.