
- •Электрический заряд и его свойства. Электрическое поле. Напряженность и индукция электрического поля. Закон Кулона. Теорема Гауса.
- •Напряженность электрического поля точечного заряда. Принцип суперпозиции. Примеры расчета электрического поля распределенных зарядов.
- •3) Применение теоремы Гаусса для расчета электрического поля заряженных тел
- •Потенциал электростатического поля. Циркуляция напряженности электрического поля. Работа перемещения заряда в электрическом поле. Энергия системы электрических зарядов.
- •Уравнение Пуассона
- •Примеры расчёта потенциала электрического поля для распределённых зарядов.
- •Электрический диполь. Поле электрического диполя. Силы, действующие на диполь в электрическом поле. Энергия электрического диполя в электрическом поле.
- •Диэлектрики в электрическом поле. Связанные заряды. Поляризованность. Диэлектрическая проницаемость и восприимчивость. Электрическое смещение.
- •9. Напряжённость и индукция электрического поля на границе раздела двух сред. Преломление линии электрического поля.
- •10. Распределение зарядов на проводящих телах. Электрическое поле вблизи поверхности заряженного проводника. Потенциал и энергия заряженного проводящего тела.
- •11. Электроёмкость. Конденсаторы. Примеры расчёта ёмкости конденсатора.
- •12. Объёмная плотность энергии электрического поля. Энергия электрического поля и работа поляризации диэлектрика.
- •13. Ток проводимости. Условия возникновения тока проводимости. Сила и плотность тока.
- •14. Уравнение непрерывности.
- •15. Сторонние силы. Электродвижущая сила. Электрическая цепь. Закон Ома и Джоуля-Ленца. Однородный и неоднородный участок цепи. Разность потенциалов и падение напряжения.
Электрический заряд и его свойства. Электрическое поле. Напряженность и индукция электрического поля. Закон Кулона. Теорема Гауса.
Электрический заряд – это физическая величина, характеризующая электромагнитное взаимодействие.
Свойства.
1)Существование в двух видах. Отрицательные и положительные. Разноименные заряды притягиваются, одноименные отталкиваются. Носителем элементарного, т.е. наименьшего, отрицательного заряда является электрон, заряд которого qe= -1,6*10-19Кл, а масса mе=9,1*10-31кг. Носителем элементарного положительного заряда является протон qр=+1,6*10-19Кл, масса mр=1,67*10-27кг.
2)Дискретность(квартование) электрического заряда. Это означает, что заряд любого тела кратен заряду электрона q=Nqe, где N – целое число.
3) Закон сохранения зарядов – в замкнутой системе алгебраическая сумма зарядов не изменяется.
4)Релятивистская инвариантность заряда. В любой ИСО с какой бы скоростью она не двигалась заряд сохраняется.
5) Единица заряда в СИ – кулон (Кл). По определению, 1 кулон равен заряду, протекающему через поперечное сечение проводника за 1 с при силе тока 1 А.
Электрическое поле — совокупность неподвижных зарядов.
Сила
взаимодействия зарядов - сила центральная,
т. е. направлена вдоль прямой,
соединяющей заряды (рис. 1.1). Для
изотропной среды закон Кулона записывается
следующим образом:
![]()
|
где k – коэффициент пропорциональности; q1 и q2 - величины взаимодействующих зарядов; r – расстояние между ними; r – радиус-вектор, проведенный от одного заряда к другому и направленный к тому из зарядов, на который действует сила.
Формулировка закона Кулона: «Сила электростатического взаимодействия между двумя точечными электрическими зарядами прямо пропорциональна произведению величин зарядов, обратно пропорциональна квадрату расстояния между ними и направлена вдоль соединяющей их прямой так, что одноименные заряды отталкиваются, а разноименные притягиваются».
Точечным зарядом называется заряженное тело, размерами которого можно пренебречь по сравнению с расстояниями до других тел, несущих электрический заряд.
Закон Кулона для изотропной и однородной среды записывается в виде
![]()
Напряженность электрического поля
Силовой характеристикой электрического поля служит напряженность E. Если на находящийся в некоторой точке заряд q0 действует сила F, то напряженность электрического поля Е равна: Е=F/q0. Графически силовые поля изображают силовыми линиями. Силовая линия – это линия, касательная, в каждой точке которой совпадает с вектором напряженности электрического поля в этой точке.
Однородное электрическое поле – это такое поле, во всех точках которого напряженность имеет одно и то же абсолютное значение и направление. П: две разноимённо заряженные металлические пластины. Если на заряд действуют одновременно несколько электрических полей, то напряженность поля равна векторной сумме напряженностей всех полей (принцип суперпозиции):
Индукция
электрического поля. Часто
бывает удобно исследовать электрическое
поле, рассматривая только заряды и их
расположение в пространстве, не принимая
во внимание свойств окружающей среды.
Для этой цели используется векторная
величина, которая называется электрической
индукцией или электрическим
смещением. Вектор электрической
индукции D в однородной
изотропной среде связан с вектором
напряженности Е соотношением![]() .
Единицей измерения индукции электрического
поля служит 1 Кл/ м2. Направление
вектора электрического смещения
совпадает с вектором Е. Графическое
изображение электрического поля можно
построить с помощью линий электрической
индукции по тем же правилам,
что и для линий напряженности.
.
Единицей измерения индукции электрического
поля служит 1 Кл/ м2. Направление
вектора электрического смещения
совпадает с вектором Е. Графическое
изображение электрического поля можно
построить с помощью линий электрической
индукции по тем же правилам,
что и для линий напряженности.
Поток
вектора напряженности электрического
поля. ![]()
Поток вектора электрической индукции. Поток вектора электрической индукции определяется аналогично потоку вектора напряженности электрического поля dFD = D dS.
Теорема
Гаусса. Рассмотрим точечный
положительный электрический заряд q,
находящийся внутри произвольной
замкнутой поверхности S (рис.
1.3). Поток вектора индукции через элемент
поверхности dS равен![]() (1.4)
(1.4)
Составляющую dSD = dS cosa элемента поверхности dS в направлении вектора индукции D рассматриваем как элемент сферической поверхности радиуса r, в центре которой расположен заряд q.
|
Учитывая,
что dSD / r2 равен элементарному
телесному углу dw, под которым из точки
нахождения заряда q виден
элемент поверхности dS,
преобразуем выражение (1.4) к виду dFD = qdw /
4p, откуда после интегрирования по всему
окружающему заряд пространству, т. е. в
пределах телесного угла от 0 до 4p, получим
F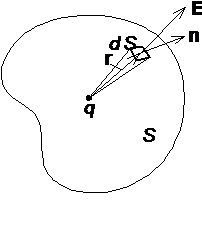 D = q.
Теорема
Гаусса:
поток
вектора электрической индукции через
замкнутую поверхность произвольной
формы равен суммарному заряду в объеме,
охваченном этой поверхностью, и не
зависит от зарядов, расположенных вне
рассматриваемой поверхности.
Основные формулы т. Гаусса:
D = q.
Теорема
Гаусса:
поток
вектора электрической индукции через
замкнутую поверхность произвольной
формы равен суммарному заряду в объеме,
охваченном этой поверхностью, и не
зависит от зарядов, расположенных вне
рассматриваемой поверхности.
Основные формулы т. Гаусса:
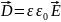

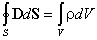 Из
теоремы Гаусса следует важное свойство
электрического поля: силовые
линии начинаются или заканчиваются
только на электрических зарядах или
уходят в бесконечность.
Из
теоремы Гаусса следует важное свойство
электрического поля: силовые
линии начинаются или заканчиваются
только на электрических зарядах или
уходят в бесконечность.
Дифференциальная
форма теоремы Гаусса. Отметим,
что интегральная
форма теоремы
Гаусса характеризует соотношения между
источниками электрического поля
(зарядами) и характеристиками электрического
поля (напряженностью или индукцией) в
объеме V произвольной,
но достаточной для формирования
интегральных соотношений, величины.
Производя деление объема V
на
малые объемы Vi ,
получим выражение![]() справедливое как
в целом, так и для каждого слагаемого.
Преобразуем полученное выражение
следующим образом:
справедливое как
в целом, так и для каждого слагаемого.
Преобразуем полученное выражение
следующим образом:
![]() (1.7)
и рассмотрим предел, к которому стремится
выражение в правой части равенства,
заключенное в фигурных скобках, при
неограниченном делении объема V.
В математике этот предел
называют дивергенцией вектора
(в данном случае вектора электрической
индукции D):
(1.7)
и рассмотрим предел, к которому стремится
выражение в правой части равенства,
заключенное в фигурных скобках, при
неограниченном делении объема V.
В математике этот предел
называют дивергенцией вектора
(в данном случае вектора электрической
индукции D):
![]() Дивергенция
вектора D в
декартовых координатах:
Дивергенция
вектора D в
декартовых координатах:
![]() Таким образом, выражение
(1.7) преобразуется к виду:
Таким образом, выражение
(1.7) преобразуется к виду:
![]()
Учитывая,
что при неограниченном делении сумма
в левой части последнего выражения
переходит в объемный интеграл, получим
![]()
Полученное соотношение должно выполняться для любого произвольно выбранного объема V. Это возможно лишь в том случае, если значения подынтегральных функций в каждой точке пространства одинаковы. Следовательно, дивергенция вектора D связана с плотностью заряда в той же точке равенством
![]() или
для вектора напряженности электростатического
поля
или
для вектора напряженности электростатического
поля![]() Эти равенства выражают теорему Гаусса
в дифференциальной
форме.
Эти равенства выражают теорему Гаусса
в дифференциальной
форме.
![]() .
.
Последнее выражение называется формулой Гаусса - Остроградского и связывает интеграл по объему от дивергенции вектора с потоком этого вектора сквозь замкнутую поверхность, ограничивающую объем.
