Свойства смешанного произведения:

 

            1)Смешанное произведение равно нулю, если:

                        а)хоть один из векторов равен нулю;

                        б)два из векторов коллинеарны;

                        в)векторы компланарны.

            2)

            3)

            4)

Аналитическая геометрия

1. Прямая на плоскости. Нормальные уравнения прямой нормальный вектор прямой. Прямая и уравнение первой степени.

Общее уравнение 

Ax + By + C (  > 0).

     Вектор   = (А; В) - нормальный вектор прямой.

     В векторном виде:   + С = 0, где   - радиус-вектор произвольной точки на прямой

Нормальное уравнение прямой. Расстояние от точки до прямой

Пусть на плоскости хОу дана прямая. Проведем через начало координат перпендикуляр к данной прямой и назовем его нормалью. Обозначим через Р точку пересечения нормали с данной прямой и установим положительное направление нормали от точки О к точке Р.

Если   - полярный угол нормали, р - длина отрезка   (рис.), то уравнение данной прямой может быть записано в виде

;

уравнение этого вида называется нормальным.

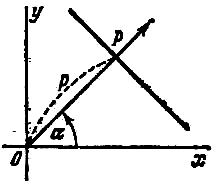
Пусть дана какая-нибудь прямая и произвольная точка  ; обозначим через d расстояние от точки М* до данной прямой. Отклонением   точки   от прямой называется число +d, если данная точка и начало координат лежат по разные стороны от данной прямой, и -d, если данная точка и начало координат расположены по одну сторону от данной прямой. (Для точек, лежащих на самой прямой,  =0). Если даны координаты  ,   точки   и нормальное уравнение прямой  , то отклонение   точки  от этой прямой может быть вычислено по формуле

.

Таким образом, чтобы найти отклонение какой-нибудь точки   от данной прямой, нужно в левую часть нормального уравнения этой прямой вместо текущих координат подставить координаты точки  . Полученное число будет равно искомому отклонению.

Чтобы найти расстояние d от точки до прямой, достаточно вычислить отклонение и взять его модуль:  .

Если дано общее уравнение прямой  , то, чтобы привести его к нормальному виду, нужно все члены этого уравнения умножить на нормирующий множитель  , определяемый формулой

.

Знак нормирующего множителя выбирается противоположным знаку свободного члена нормируемого уравнения.

2. Уравнение прямой на плоскости, проходящей через заданную точку, перпендикулярно данному вектору.

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору n (3, -1)

Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.

Получаем: 3 – 2 + C = 0, следовательно С = -1.

Итого: искомое уравнение: 3х – у – 1 = 0.

3. Расстояние от точки до прямой на плоскости.

Расстояние от точки до прямой

Длина перпендикуляра, опущенного из данной точки на прямую, называется расстоянием от дочки до прямой.