Векторная алгебра

1. Понятие вектора. Линейные операции над векторами: сложение векторов и умножение на число. Линейные свойства векторов. Примеры.

Величины, которые характеризуются, не только числом, но еще и направлением, называются векторными величинами или просто векторами. Векторами являются, например, скорость, ускорение, сила.

Сложение векторов

Под параллельным переносом вдоль вектора понимают перемещение всех точек пространства в одном направлении на одинаковое расстояние. Определим сложение векторов так, чтобы последовательные сдвиги вдоль двух векторов соответствовали сдвигу вдоль суммы этих векторов.

Пусть даны два вектора   и  . Приложим вектор   к некоторой точке  , получим  . Приложим вектор   к точке  , получим  . Тогда вектор   будем называть суммой векторов:  .

Докажем, что данное определение не зависит от выбора точки  .

Приложим вектор   к другой точке  , получим  . Приложим вектор   к точке  , получим  .

Рассмотрим направленные отрезки   и  . Они, очевидно, равны (см. рис.), поскольку   — параллелограмм.

Умножение на число

Произведением вектора   на число   называется вектор, который:

1. коллинеарен вектору  ;

2. сонаправлен ему, если  , или противоположнонаправлен, если  ;

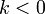3. длины связаны следующим соотношением:  .

Данное определение согласовано с определением сложения:

для любого натурального  .

Свойства линейных операций

Сложение векторов коммутативно:  .

Сложение векторов ассоциативно:  .

Прибавление нулевого вектора к любому не меняет последнего:  . Очевидно,  .

Для любого вектора   существует вектор   такой, что   или  .

Умножение вектора на число ассоциативно:  . Умножение вектора на число дистрибутивно относительно сложения чисел:  .

Доказательство сводится к перечислению всех возможных знаков   и  , в каждом случае утверждение очевидно.

Умножение вектора на число дистрибутивно относительно сложения векторов:  . Это следует из подобия треугольников   и   на рисунке.

Очевидно, умножение на единицу не меняет вектор:  .

2. Координаты и компоненты вектора. Линейные операции над векторами в координатах. Примеры.

Если   и   — два неколлинеарных вектора в плоскости, а   — произвольный вектор в той же плоскости, то всегда существуют такие числа   и  , что  . В этом случае говорят, что вектор   разложен по векторам   и  .

Если   и   — неколлинеарные единичные векторы (т. е. вектора, модуль которых равен единице)  , то произвольный вектор   плоскости может быть представлен в виде  . В этом случае говорят, что вектор   имеет в системе   и   координаты  .

Если векторы   и   взаимно перпендикулярны, причем вектор   может быть получен из вектора   поворотом против часовой стрелки, то говорят, что прямые, в которых лежат   и  , образуют декартову прямоугольную систему координат, а числа   называются декартовыми координатами вектора  .

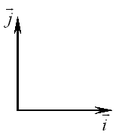
Пусть точка   с координатами   — начало вектора  , а точка   с координатами   — его конец. Тогда координаты вектора связаны с координатами точек   и  формулами:  ,  , т. е. декартовы координаты вектора равны разности соответствующих координат конца вектора и его начала.

Декартовы координаты вектора   являются проекциями этого вектора на соответственные оси систем координат:  ,  .

Пусть вектор   имеет координаты  , что записывается в виде  , а вектор   —  , или  .

Тогда:

,

,

,

,

т. е. действиям с векторами отвечают идентичные действия с их координатами.

Модуль вектора   определяется через его декартовы координаты посредством равенства:  , а единичный вектор  , имеющий с вектором   одинаковое направление, записывается в виде   и имеет координаты: 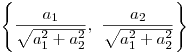 .