- •[Править]Определение
- •13) Вторая производная и ее физический смысл
- •Физический смысл второй производной
- •24) Определение вектора
- •Равенство двух векторов
- •Действие над векторами и их свойства
- •Сфера в трёхмерном пространстве
- •Аксиомы стереометрии и их следствия
- •Перпендикулярные прямые
- •[Править]Построение перпендикуляра
- •[Править]Координаты точки основания перпендикуляра к прямой
- •Двугранный угол
- •Угол между плоскостями
Перпендикулярные прямые
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
В
аналитическом выражении прямые, заданные
линейными функциями ![]() и
и ![]() будут
перпендикулярны, если выполнено
условие
будут
перпендикулярны, если выполнено
условие ![]() .
Эти же прямые будут перпендикулярны,
если
.
Эти же прямые будут перпендикулярны,
если ![]() .
(Здесь
.
(Здесь ![]() —
углы наклона прямой к горизонтали)
—
углы наклона прямой к горизонтали)
Для
обозначения перпендикулярности имеется
общепринятый символ: ![]() ,
предложенный в 1634
году французским
математиком Пьером
Эригоном.
,
предложенный в 1634
году французским
математиком Пьером
Эригоном.
[Править]Построение перпендикуляра

![]()
Построение перпендикуляра
Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А' и В'.
Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A' и В' соответственно, проходящими через точку Р. Кроме точки Р есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: (синий) Соединяем точки Р и Q. PQ и есть перпендикуляр к прямой АВ.
[Править]Координаты точки основания перпендикуляра к прямой
A(xa,ya) и B(xb,yb) — прямая, O(xo,yo) — основание перпендикуляра, опущенного из точки P(xp,yp).
xo = (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) / ((yb-ya)^2+(xb-xa)^2);
yo = (yb-ya)*(xo-xa)/(xb-xa)+ya.
Признак перпендикулярности прямой и плоскости
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И ПЛОСКОСТИ. Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости. |
|
Доказательство:
Пусть а прямая,
перпендикулярная прямым b и c в
плоскости |
|
35)теорема о трёх перпендикулярах
О ТРЕХ ПЕРПЕНДИКУЛЯРАХ. Если прямая, проведенная на плоскости черезоснование наклонной, перпендикулярна еепроекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной. |
|
Доказательство: Пусть АВ -
перпендикуляр плоскости
, АС -
наклонная и с -
прямая в плоскости
,
проходящая через основание С.
Проведем
прямую СA1,
параллельную прямой АВ.
Она перпендикулярна плоскости
.
Проведем через прямые АВ и СA1 плоскость |
|
36) признак перпендикулярности плоскостей
ПРИЗНАК ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ. Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны. |
|
Доказательство: Пусть
-
плоскость , b -
перпендикулярная ей прямая,
-
плоскость проходящая через прямую b,
и с -
прямая по которой пересекаются
плоскости
и
.
Докажем, что плоскости
и
перпендикулярны.
Проведем
в плоскости
через
точку пересечения прямой b с
плоскостью
прямую а,
перпендикулярную прямой с.
Проведем через прямые а и bплоскость |
|
37) связь между параллельностью и перпендикулярностью плоскостью
Определение 3.3.
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.
Т еорема 3.1. Признак перпендикулярности прямой и плоскости.
Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.
Доказательство
|
Сформулируем некоторые теоремы, устанавливающие связь между параллельностью и перпендикулярностью в пространстве.
Т еорема 3.2.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.
|
|
Чертеж 3.2.2. |
Т еорема 3.3.
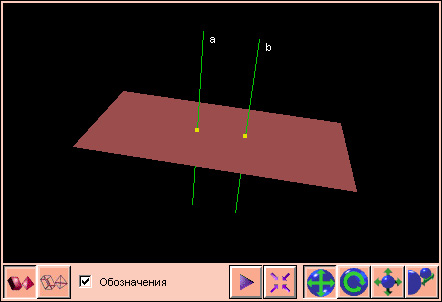
Две прямые, перпендикулярные одной плоскости, параллельны между собой.
Т еорема 3.4.
Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.
Т еорема 3.5.
Две плоскости, перпендикулярные одной прямой, параллельны между собой.
|
|
Чертеж 3.2.3. |
Докажите
эти теоремы самостоятельно, используя
такое свойство: если векторы ![]() коллинеарные
и
коллинеарные
и ![]() то
то ![]()
О пределение 3.4.
Перпендикуляром, проведенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной данной плоскости, который соединяет данную точку с точкой плоскости.
|
38) двугранный угол