24) Определение вектора

Рассмотрим на плоскости две точки A и B. Обозначим через  вектор AB, понимая под этим направленный отрезок AB, т. е. отрезок, у которого точка A является началом, а точка B -- концом . Таким образом, точки A и B, ограничивающие вектор   , играют различную роль. Именно в этом в первую очередь и состоит главное различие между вектором   и отрезком AB. Две точки A и B плоскости задают два различных вектора   и  одинаковой длины и противоположно направленные.

Равенство двух векторов

Два вектора   и   , расположенные на одной прямой, считаются равными, если равны отрезки AB и CD, т. е. равны длины этих векторов, а лучи AB и CD задают одинаковые направления. Если же векторы   и   не расположены на одной прямой, то они считаются равными, если четырехугольник ABDC (вершины рассматриваются в данном порядке) является параллелограммом. Таким образом, мы можем вектор не только перемещать вдоль соответствующей прямой, но и переносить его начало в любую точку плоскости. Следовательно, для обозначения вектора нет необходимости указывать его начало и конец, и можно использовать обозначения вида a , b ,l   и т. п., помещая в случае необходимости начало соответствующего вектора в удобную точку плоскости. Для длины вектора a будем использовать обозначение | a | - читается: "длина вектора a" или "модуль вектора a"

Действие над векторами и их свойства

Ключевые слова: вектор, сумма, разность векторов, координаты вектора

Вектор - это направленный отрезок. 

Суммой векторов − a(a1;a2) и − b(b1;b2) называется вектор − c a1+b1;a2+b2  ,  т.е. − a a1;a2 +− b b1;b2 =− c a1+b1;a2+b2  .

Для любых векторов − a(a1;a2)  и − b(b1;b2) справедливы равенства:

• переместительный закон: − a+− b=− b+− a;

• сочетательный закон: − a+(− b+− c)=(− a+− b)+− c;

• из переместительного и сочетательного законов следует, что, складывая любое число векторов, можно как угодно переставлять и группировать слагаемые.

Каковы бы ни были три точки A , B и C , имеет место векторное равенство −− AB+−− BC=−− AC

Разностью векторов − a(a1;a2) и − b(b1;b2) называют такой вектор − c(c1c2), который в сумме с вектором − b(b1;b2) дает вектор − a(a1;a2). Таким образом: − c(c1c2) + − b(b1;b2) = − a(a1;a2), откуда c₁ =a₁ - b₁ и c₂ = a₂ - b_2.

Произведением вектора − a(a1;a2) на число   называется вектор − b(b1;b2), такой что  b₁ =  a₁ и b₂ =  a₂. т.е.  − a(a1;a2)=− b( a1; a2).

Скалярным произведением двух ненулевых векторов называют произведение длин этих векторов на косинус угла между ними:  S=− a − b= − a − b cos  , если угол между векторами равен 

25) Скаля́рное произведе́ние — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины данного вектора x на проекцию другого вектора y на данный вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Обычно используется одно из следующих обозначений:

,

,

,

или (обозначение Дирака, часто применяемое в квантовой механике для векторов состояния):

.

Обычно предполагается что скалярное произведение положительно определено, то есть

 для всех  .

Если этого не предполагать, то произведение называется индефинитным.

26) прямоугольная система координат

Прямоугольная система координат - прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению.

Связанные термины: Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям, а общей Декартовой системой координатназывают аффинную систему координат (не прямоугольную). ^[1]

Действие над векторами, заданными координатами

Теорема 3. Пусть на плоскости выбран векторный базис   ,   и относительно него векторы  и   заданы своими координатами:  . Тогда  , т. е. при сложении или вычитании векторов  складываются или вычитаются их одноименные координаты;  , т. е. при умножении вектора на число его координаты умножаются на это число. Теорема 3. Пусть на плоскости выбран векторный базис   ,   и относительно него векторы  и   заданы своими координатами:  . Тогда  , т. е. при сложении или вычитании векторов  складываются или вычитаются их одноименные координаты;  , т. е. при умножении вектора на число его координаты умножаются на это число.

Длина вектора Векторы Обозначения:   Длина вектора, модуль (абсолютная величина): 

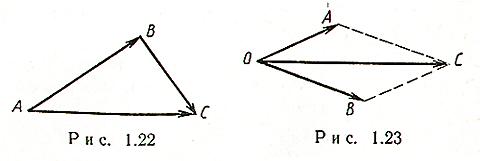
     Сумма векторов:

       (правило треугольника) (рис. 1.22);

       (правило параллелограмма) (рис. 1.23);

       (правило многоугольника);

       (правило параллелепипеда,   - диагональ).

     Разность векторов: 

     Формула вычитания векторов:   (рис. 1.24).

     Признак коллинеарности векторов: 

27)векторы в пространстве и действия над ними

Вектором наз. упорядоченная совокупность чисел Х={X₁,X₂,...X_n} вектор дан в n-мерном пространстве. Т(X₁,X₂,X₃). n=1,2,3. Геометрический вектор - направленный отрезок. |AB|=|a| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.

1.умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми: а) А||В. б) l>0, то А­­В, l<0, то А­¯В. в)l>1, то А<<span style="TEXT-DECORATION: underline">В, )l<1, то АВ. 2. Разделить вектор на число n значит умножить его на число, обратное n: а/n=a*(1/n).

3.Суммой неск-их векторов а и в наз. соединяющий начало 1-го и конец последнего вектора. 4. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор а.

Скалярное произведение Определение 9.15. 

Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a, либо на прямой, параллельной a.

О пределение 9.16. 

Углом между ненулевыми векторами называется угол между прямыми, для которых данные вектора являются направляющими. Угол между любым вектором и нулевым вектором по определению считаем равным нулю. Если угол между векторами равен 90°, то такие вектора называются перпендикулярными. Угол между векторами будем обозначать так: 

О пределение 9.17. 

Скалярным произведением векторов   и   называется произведение их длин на косинус угла между ними: 

28) уравнение прямой и плоскости

Определение. Любая прямая на плоскости может быть задана уравнением первого порядка

Ах + Ву + С = 0,

причем постоянные А, В не равны нулю одновременно, т.е. А² + В²  0. Это уравнение первого порядка называют общим уравнением прямой.

 

            В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

-          C = 0, А  0, В  0 – прямая проходит через начало координат

-          А = 0, В  0, С  0 { By + C = 0}- прямая параллельна оси Ох

-          В = 0, А  0, С  0 { Ax + C = 0} – прямая параллельна оси Оу

-          В = С = 0, А  0 – прямая совпадает с осью Оу

-          А = С = 0, В  0 – прямая совпадает с осью Ох

Уравнение сферы

 Сфе́ра (греч. σφαῖρα — мяч) — замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учетом непостоянства значения размеров дуг составляет 41252.96 кв. градусов.

Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностьюшара.

Объёмы цилиндра, вписанной в него сферы, касающейся его основания, и двух конусов, имеющих общую вершину в центре основания и основания, равные основаниям цилиндра, находятся в соотношении 1:2:3^[1]

Площадь сферы

Объем шара, ограниченного сферой

Площадь сегмента сферы

 , где H — высота сегмента, а   — зенитный угол