8. Линейные дифференциальные уравнения второго порядка. Пространство решений. Фундаментальная система решений.

Определение 1. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

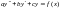, (1)

где a,b,c - числа и 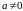.Если f(x)=0, то уравнение (1) называют однородным . В противном случае - неоднородным .Теорема 1. Если функция f (x) непрерывна на отрезке [d,e], то для любой точки 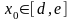и любой пары чисел 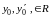уравнение (1) имеет единственное решение, удовлетворяющее начальным условиям

и определенное на всем отрезке [d,e].

2. Однородное уравнение.

Обозначим через S_L множество решений однородного уравнения :

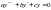. (4)Cледствием предыдущей теоремы является следующая теорема.Теорема 2. Множество S_L является линейным пространством функций, определенных на всей прямой и Определение. Функции y=y₁(x) и y=y₂(x), определенные при всех x, называются линейно-зависимыми, если  C₁, C₂ такие , чтоC₁²+C₂²  0 и C₁ y₁(x) + C₂y₂(x) = 0  x.В противном случае функции y₁ и y₂ называются линейно-независимыми .Из теоремы 2 следует, что базис в пространстве решений S_L состоит из двух линейно-независимых решений.Определение. Базис в пространстве решений S_L называется фундаментальной системой решений (в дальнейшем ФСР).Следствие . Если y₁ ,y₂ есть линейно-независимые решения уравнения (4), то есть ФСР , то общее решение является линейной комбинацией y₁ и y₂, то есть задается формулой y = C₁y₁ + C₂y₂ .

Таким образом, решение уравнения (4) свелось к отысканию ФСР. Решение этой задачи связано с корнями квадратного трехчлена: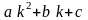 . (5)

Определение. Многочлен (5) и уравнение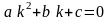 . (6)называются характеристическими.

Обозначим 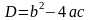- дискриминант уравнения (6).

Теорема 3.

1. Если 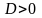и k₁ , k₂ есть действительные различные корни уравнения (6), то функции :

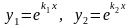(7)

являются ФСР и 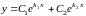есть общее решение уравнения (4).

2. Если 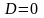и к есть единственный действительный корень уравнения (6), то функции :

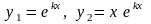являются ФСР и

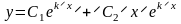есть общее решение (4).

3. Если 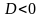, то функции:

(8)

являются ФСР и 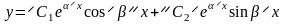есть общее решение уравнения (4). Здесь Пример. Решить задачу Коши:

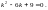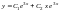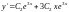Найдем сначала общее решение уравнения (9). Для этого составим харак-теристическое уравнение Оно имеет единственный действи-тельный корень k =3. Поэтому, согласно теореме общее решение уравнения (9) имеет вид: . Подставив в это равенство начальное условие (10), получим C₁= 0. Следовательно , y = C₂ x e^3x . Найдем производную .Отсюда и начального условия (11) найдем C₂ = 2.

Ответ: y=2xe^3x.