
- •2. Общее и частное решение.
- •2.Дифференциальные уравнения с разделяющимися переменными
- •Это уравнение с разделяющимися переменными, где
- •3. Однородные уравнения
- •4. Линейные уравнения и уравнения Ьернулли.
- •5. Экономическая модель Эванса
- •6.Экономическая модель Соллоу. Золотое правило экономики
- •7. Дифференциальные уравнения второго порядка. Понижение порядка. Примеры.
- •2. Дифференциальные уравнения второго порядка, которые приводятся к уравнениям первого порядка.
- •Это уравнение приводится к уравнению (n-k)-го порядка
- •8. Линейные дифференциальные уравнения второго порядка. Пространство решений. Фундаментальная система решений.
- •9. Неоднородные линейные дифференциальные уравнения второго порядка.
- •10. Числовые ряды. Сумма рде и се свойства. Необходимое условие сходимости. Геометрическая прогрессия
- •11. Ряды со знакопеременными членами. Абсолютная сходимость. Пришак Лейбница
- •12. Ряды со знакопеременными членами. Абсолютная сходимость. Пришак Лейбница
- •13. Функциональные рядЫ. При шахи Коши и Даламбсра для знакопеременных рядов.
- •14. Степенные ряды. Радиус и интервал сходимости. Формула Коши и Даламбсра для радиуса сходимости
- •15. Свойства степенных рядов. Разложение функции в ряд Тейлора
- •17.Комплексные числа.Операции над ними.
- •18. Тригонометрическая форма записи. Умножение и деление в тригонометрической форме. Формула Муавра. .
6.Экономическая модель Соллоу. Золотое правило экономики
Экономика рассматривается как единое целое (без структурных подразделений), в ней производится единственный универсальный продукт, который может потребляться как в непроизводственной сфере, так и в производственной; потребление его в производственной сфере может рассматриваться как инвестирование (с некоторой натяжкой таким “продуктом” может выступать денежная оценка всего и вся). Эта модель достаточно адекватно отражает важнейшие макроэкономические аспекты, в том числе и процесса воспроизводства ([14]).В модели Солоу экономика описывается пятью параметрами, которые зависят от времени t:
 –
конечный
продукт (выраженный в денежном выражении),
–
конечный
продукт (выраженный в денежном выражении),
 – трудовые
ресурсы,
– трудовые
ресурсы,
 – производственные фонды,
– производственные фонды, – инвестиции в производство,
– инвестиции в производство, – размер непроизводственного
потребления.Конечный продукт
– размер непроизводственного
потребления.Конечный продукт
 используется на инвестиции и
непроизводственное потребление
используется на инвестиции и
непроизводственное потребление
 ,
то есть
,
то есть
 Обозначим
Обозначим
 – доля конечного продукта, вкладываемая
в инвестиции. Тогда
– доля конечного продукта, вкладываемая
в инвестиции. Тогда
 Таким образом
Таким образом
 и
и
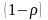 есть доли инвестиций и непроизводственного
потребления в конечном продукте. Легко
видеть, что
,
есть доли инвестиций и непроизводственного
потребления в конечном продукте. Легко
видеть, что
,
 Предположим,
что конечный продукт
выражается производственной функцией
Кобба – Дугласа:
Предположим,
что конечный продукт
выражается производственной функцией
Кобба – Дугласа:
 ,где
,где
 ,
α есть положительные константы и
,
α есть положительные константы и

 .
В примере 2 на странице 23 было показано,
что
равняется коэффициенту эластичности
производственной функции по фондам.Будем
считать, что прирост трудовых ресурсов
пропорционален наличным трудовым
ресурсам и длительности этого прироста
с коэффициентом пропорциональности
.
В примере 2 на странице 23 было показано,
что
равняется коэффициенту эластичности
производственной функции по фондам.Будем
считать, что прирост трудовых ресурсов
пропорционален наличным трудовым
ресурсам и длительности этого прироста
с коэффициентом пропорциональности
 Пусть
Пусть
 есть коэффициент выбытия производственных
фондов. Тогда
есть коэффициент выбытия производственных
фондов. Тогда

 При
получим
При
получим
 Таким образом, модель Солоу описывается
системой уравнений:
Таким образом, модель Солоу описывается
системой уравнений:
 ;
(6)
;
(6)
 (7)
(7)
 (8)
(8)

 (10
(10 (11)
(11)
 .
(12)
.
(12)
Здесь
 есть значения
есть значения
 и
и
 в
начальный момент времени
.
Решим вначале задачу Коши (9), (10) по плану
на странице 31. 1) Приравняв к нулю правую
часть (9), получим частное решение
в
начальный момент времени
.
Решим вначале задачу Коши (9), (10) по плану
на странице 31. 1) Приравняв к нулю правую
часть (9), получим частное решение
 ,
которое не удовлетворяет начальному
условию (10), поскольку
,
которое не удовлетворяет начальному
условию (10), поскольку
 .
2) При
.
2) При
 разделим переменные и в соответствии
с теоремой 1 на странице 31 запишем общий
интеграл уравнения (9):
разделим переменные и в соответствии
с теоремой 1 на странице 31 запишем общий
интеграл уравнения (9):
 =
=
 .
Отсюда
.
Отсюда
 ;
;
 ;
;
 ,
где
,
где
 .
При
из (10) получим
.
При
из (10) получим
 Следовательно,
Следовательно,
 .
(13)
.
(13)
Обозначим
 - средняя фондовооруженность,
- средняя фондовооруженность,
 - средняя производительность труда.
Выразим
- средняя производительность труда.
Выразим
 и подставим в (11):
и подставим в (11):
 .
Воспользовавшись (9) и сократив на
,
получим задачу Коши:
.
Воспользовавшись (9) и сократив на
,
получим задачу Коши:
 (14)
(14)
 ,
(15)
,
(15)
где
 Найдем общее решение уравнения с
разделяющимися переменными (14) по плану
на странице 31. 1) Решим уравнение
Найдем общее решение уравнения с
разделяющимися переменными (14) по плану
на странице 31. 1) Решим уравнение

 Данное уравнение имеет два решения
Данное уравнение имеет два решения
 и
и
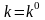 ,
где
,
где
 (16)
(16)
Стационарное решение не удовлетворяет начальному условию (15).
Рассмотрим
стационарное решение
.
Из (13) выведем

 ;
;
 Таким образом, на стационарной траектории
все основные показатели растут
экспоненциально, пропорционально
трудовым ресурсам ([14]).
Таким образом, на стационарной траектории
все основные показатели растут
экспоненциально, пропорционально
трудовым ресурсам ([14]).
2)
При
 разделим переменные и напишем общий
интеграл уравнения (14):
разделим переменные и напишем общий
интеграл уравнения (14):
 (17)
(17)
Обозначим
 (18)
(18)
Тогда




Отсюда и (17) следует

 (19)
(19)
где
 Равенство (19) задает общее решение
уравнения (14). Из (18), (16) следует, что
частое решение
входит
в семейство (19) при
.
Равенство (19) задает общее решение
уравнения (14). Из (18), (16) следует, что
частое решение
входит
в семейство (19) при
.
Положив в (19) t = 0 и воспользовавшись (16), (18), найдем

Так
как
 то
из (19) выведем,
то
из (19) выведем,
 (20)
(20)
Таким
образом, для любого начального значения
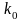 средняя фондовооруженность сходится
к стационарному значению
средняя фондовооруженность сходится
к стационарному значению
 ([14]).
Обозначим
([14]).
Обозначим
 удельное
потребление (на одного работника).
Учитывая, то что
удельное
потребление (на одного работника).
Учитывая, то что
 из (8),(20) выведем
из (8),(20) выведем
 ,
,
 ,
(21)
,
(21)
где

 Обозначим
Обозначим
 Принято считать, что чем больше удельное
потребление с,
тем общество богаче и экономика
развивается успешнее. Найдем при какой
доле инвестиций
предельное удельное потребление
Принято считать, что чем больше удельное
потребление с,
тем общество богаче и экономика
развивается успешнее. Найдем при какой
доле инвестиций
предельное удельное потребление
 достигает наибольшее значение. Для
этого найдем
достигает наибольшее значение. Для
этого найдем
 . Вычислим
. Вычислим

 ,
,
поскольку
 Следовательно, на интервале
Следовательно, на интервале
 есть только одна критическая точка
есть только одна критическая точка
 Подсчитаем значения
Подсчитаем значения
 в критической точке
и на концах отрезка
в критической точке
и на концах отрезка


Поэтому
 и этот максимум достигается при
и этот максимум достигается при

Данное равенство представляет собой Золотое правило экономики:Чтобы экономика развивалась наиболее успешно доля инвестиций от валового продукта должна равняться коэффициенту элластичности функции Кобба-Дугласа по фондам.
