21. Моделирование равномерно распределенных случайных величин.

Определение. Непрерывная СВ γ имеет непрерывное равномерное распределение в интервале[a; b], если ее плотность вероятности имеет вид:

При моделировании часто используют случайные числа из интервала [0,1]. В этом случае:

Случайное число из интервала[0,1] x_i соответствует числу:

x_i' = (b–a)x_i + a

Применительно к двоичным дробям случайное число из интервала[0,1] представляет собой бесконечную дробь

Непрерывные СВ существуют только в теории.

На практике все СВ дискретны. Шаг дискретности равен наименьшей единице измерения. Сл. величина кси на интервале[0,1] принимает значения:

x_i = i / (2ⁿ - 1), i = 0,1,2,... , 2ⁿ -1.

p_i = 0,5ⁿ

22. Моделирование случайных величин с произвольным законом распределения.

В основе моделирования случайных величин с произвольными законами распр. вероятности лежит, как правило, метод обратной функции.

Теорема: (Смирнов)

Если СВ yимеет плотность распределения вероятностейf(y), то распределение случайной величины

(1)

F(y) является по определению функцией распределения СВ.

Из формулы (1)

Моделировать x_i мы умеем. Нужно найти неизвестное y_i, находящееся в верхнем пределе интеграла. Относительно y_i выражение принимает вид

y_i = F^-1(x_i) (2)

поэтому и называется метод ОФ (Смирнова)

Примеров подобного аналитического преобразования СЧ из равномерного распределения в случайное число из произвольного распределения немного, т.к. для многих законов распределения интеграл (1) относится к расходящимся, а численные методы увеличивают затраты машинного времени. Поэтому на практике используются приближенные методы формирования случайных чисел, которые могут быть разделены на специальные и универсальные. Специальные методы пригодны для получения СЧ с конкретными теоретическими законами распределения. Универсальные способы позволяют генерировать числа с любым произвольным законом распределения.

23. Моделирования единичного события.

Под единичным событием будем понимать смену состояний одного элемента или системы, причем состояний всего два. Переход из одного состояния в другое случайный. В любой момент времени система находится в одном состоянии с вероятностью P, а в другом – с вероятностью (1 – P).

Цель моделирования: имитировать состояние такого элемента.

Пусть некоторое событие Aсвершается с вероятностью P(A). Моделью свершения такого единичного события A является попадание значения x_iслучайной величины γ РРСВ в интервале [0,1] в числовой интервал [0; P(A)].

Пример: Пусть вероятность состояния элемента P(A) = 0,9. В i-той реализации x_i = 0,955. Значит, событие не свершилось.

Фрагмент алгоритма имитации:

k

24. Моделирование полной группы несовместных событий.

Элемент системы или система в целом может находиться во многих (больше двух) несовместных состояниях. Известны вероятности нахождения системы в этих состояниях. Такие события называются полной группой несовместных событий.

Алгоритм моделирования основан на следующей теореме:

Теорема:

В полной группе несовместных событий моделью свершения события A_m является попадание значения в отрезок P_m числовой шкалы , где n - число несовместных событий.

Такой способ моделирования несовместных событий обычно называют определением исхода по жребию.

Варианты алгоритмов определения исходов по жребию:

25. Моделирование совместных независимых событий.

Способ моделирования состоит в том, что совместные независимые события сводятся к одному сложному событию. Моделирование может быть выполнено двумя способами:

– определение совместных исходов выбором по жребию;

– последовательная проверка исходов.

3.1. Определение совместных исходов по жребию

По вероятностям и нужно определить вероятности возможных исходов, т. е. появления совместных независимых событий. Возможные исходы совместного события и соответствующие вероятности представлены в табл. 2.

Таблица 2

Совместное событие в -ой реализации определяется выбором исхода по жребию.

Если случайное число при очередной реализации окажется, например, на участке , то в данной реализации фиксируется свершение сложного события . Если же окажется , то фиксируется событие .

3.2. Последовательная проверка исходов

Алгоритм последовательной проверки исходов

Проверку свершения каждого из совместных событий надо осуществлять разными случайными числами, так как события независимые. При первом способе достаточно одного случайного числа , но сравнений может быть больше. Кроме того, нужно предварительно рассчитывать вероятности возможных исходов.

26. Моделирование совместных зависимых событий.

Пусть события A и B имеют вероятности свершения P(A) и P(B). Условная вероятность P(B/A) свершения события B при условии, что событие A произошло, известна. Рассмотрим алгоритм моделирования на примере.

Пример

В ремонтное подразделение поступают вышедшие из строя средства связи (СС). В каждом СС могут быть неисправными в любом сочетании блоки . Вероятности выхода из строя блоков соответственно. Ремонт производится путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС вероятности наличия исправных блоков соответственно. При отсутствии хотя бы одного из исправных блоков ремонт неисправного СС не производится.

Построить алгоритм имитационной модели с целью определения абсолютного и относительного количества отремонтированных СС с неисправными блоками и из общего количества поступивших в ремонт СС.

Решение

Для имитации неисправных блоков СС и имитации наличия исправных блоков в ремонтном подразделении воспользуемся способом определения по жребию. Для этого рассчитаем вероятности исходов и сведем их в табл. 3 и 4 соответственно.

Таблица 3

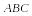
			С другими блоками
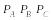
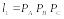
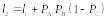
			1

Таблица 4

			С другими блоками
			1

Так как нужно определить абсолютное и относительное количества отремонтированных СС, поступивших с неисправными блоками и , то нет смысла рассчитывать вероятности для других сочетаний неисправных и исправных блоков.

В алгоритме приняты следующие обозначения:

 — заданное количество реализаций модели;

 — счетчик количества реализаций модели;

 — счетчик числа отремонтированных СС за реализаций модели;

 — абсолютное количество отремонтированных СС;

 — относительное количество отремонтированных СС.

Согласно постановке задачи в блоках 3…7 по данным табл. 3 разыгрывается, с какими неисправными блоками поступает СС в ремонт. В результате розыгрыша определяется номер интервала (столбца табл. 3) и запоминается в переменной .

Аналогично в блоках 8…11 разыгрывается по данным табл. 3.6 наличие в ремонтном подразделении необходимых блоков для замены.

Если такие блоки имеются, т. е. выполняется условие в блоке 12, в счетчик (блок 13) добавляется единица.

Алгоритм модели функционирования системы ремонта