6. Индукция и напряженность магнитного поля. Закон полного тока.

Напряжённость магни́тного по́ля — (стандартное обозначение Н) это векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.

Где -магнитная постоянная =

Намагни́ченность — векторная физическая величина, характеризующая магнитное состояние макроскопического физического тела. Обозначается обычно М или J. Определяется как магнитный момент единицы объёма вещества:

Здесь, M — вектор намагниченности; m - вектор магнитного момента; V — объём.

В общем случае (случае неоднородной, по тем или иным причинам, среды) намагниченность выражается как

и является функцией координат.

В вакууме (или в отсутствие среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряженность магнитного поля совпадает с вектором магнитной индукции.

В магнетиках (магнитных средах) напряженность магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».

Например, если поле создается катушкой с током, в которую вставлен железный сердечник, напряженность магнитного поля H внутри сердечника совпадает (в СГС точно, а в СИ - с точностью до постоянного размерного коэффициента) с вектором B0, который был бы создан этой катушкой при отсутствии сердечника и который в принципе может быть рассчитан исходя из геометрии катушки и тока в ней, ничего не зная о материале сердечника и его магнитных свойствах.

Магни́тная инду́кция — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно, — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 104 Гс

Закон полного тока

Датский физик X.Эрстед в начале 19 века определил главный в теории электромагнетизма экспериментальный факт, он заключается в следующим, протекание по проводникам электрического тока приводит к появлению в окружающем пространстве магнитного поля.

Этот факт предоставил возможность французскому выдающемуся ученому Лмперу выразить формулировкой закон, который на сегодняшний день имеет название закона полного тока.

Проанализируем рисунок ниже, воображаемый контур L в пространстве, ограничивающий поверхность S.

На этом контуре установим направление обхода так, чтобы движение с конца вектора вдоль контура элементарной площадки dS прослеживалось в направлении против часовой стрелки.

Далее представим то, что поверхность S пронизывается отдельной системой токов, которая может нести как дискретный характер (к примеру, систему отдельных проводников), так и быть непрерывно распределенной (электронный поток может послужить этому примером). Не обуславливая тем временем физической природы данных токов, будем подразумевать для конкретности, что они распределены непрерывно в пространстве с кое-какой плотностью

То теперь полный ток, пронизывающий контур, найдется в виде

Закон полного тока говорит о том, что циркуляция по контуру L вектора напряженности магнитного поля, инициированного протеканием тока равна полному току, то есть.

Закон полного тока формулирует соотношение выше в интегральной форме.

В том, чтобы связать плотность полного тока в данной гонке с напряженностью магнитного поля, то есть найти дифференциальную форму данного закона, надлежит употребить знаменитой теоремой Стикса из векторного анализа, которая говорит нам о том, что для каждого векторного поля А верно равенство

Использовав крайнюю формулу и перестроив с её помощью

будем располагать

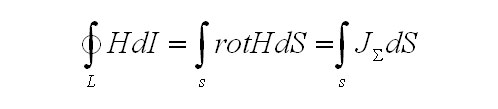
откуда получим из-за произвольности выбранного контура

Формула выше несёт в себе закон полного тока в дифференциальной форме. Заметим, что при помощи закона полного тока в интегральной форме удается разрешить ряд задач, связанных по нахождению магнитного поля заданных токов.