2.2. Расчёт главных балок пролётного строения. Определение расчётных усилий.

Постоянная нагрузка на пролётное строение складывается из собственного веса конструкции и веса мостового полотна.

Нормативная нагрузка на 1 пог.м. главной балки определяется , кН/м:

• от собственного веса

p₁= = =27,02 кН/м;

• от веса мостового полотна с ездой на балласте

р₂= = =17,64 кН/м,

где V и l_п- объём железобетона и полная длина пролётного строения;

n- число главных балок;

h_б- толщина слоя балласта;

b_б- ширина балластного корыта.

Коэффициенты надёжности по нагрузке _f для постоянных нагрузок при расчёте на прочность принимаются:

• для собственного веса конструкции _f1=1,1;

• для веса мостового полотна с ездой на балласте _f2=1,3.

При расчёте на прочность нормативная временная нагрузка по схеме СК используется в расчётах в виде

• эквивалентной нагрузки К кН/м, соответствующей наиболее тяжёлой нагрузке от состава с локомотивом;

• распределённой нагрузки 9,81К кН/м, от веса гружёных вагонов состава;

• нагрузки 13,7 кН/м от порожнего подвижного состава.

Нормативная временная вертикальная нагрузка на одну главную балку принимается равной

р_= .

Для класса нагрузки К=13 и данных линий влияния (см. рис. 3) имеем:

при α=0,25;λ=16,50м  р_1=189,20 кН/м , =25,52

при α=0,5;λ=16,50м  р_2=176,35 кН/м , =34,03

при α=0;λ=16,50м  р_3=202,05 кН/м , =8,25

при α=0;λ=8,25м  р_4=236,70 кН/м. =2,0625

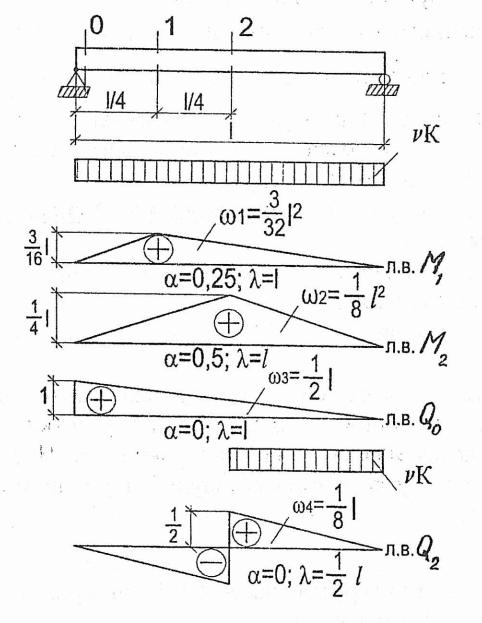
Рис.3. Линии влияния усилий в разрезной балке.

Нормативная временная нагрузка умножается при расчёте на прочность на коэффициент надёжности по нагрузке _f ,который принимает значения в зависимости от длины загружения линии влияния :

_f1= 1,3-0,003*16,5=1,25 ,

_f2=1,25 ,

_f3=1,25 ,

_f4=1,3-0,003*8,25=1,28.

Динамический коэффициент к нагрузкам от подвижного состава определяется по формуле

1+= =1+ =1,27.

Полные усилия в сечениях разрезной балки при расчёте на прочность определятся по следующим формулам:

М₁= = =9008,79 кНм;

М₂= = =11318,71 кНм;

Q₀= = =3080,62 кН;

Q₂= = =843,60 кН.

Усилия при расчёте на трещиностойкость определяются от действия на конструкцию нормативных нагрузок. Коэффициенты надёжности по нагрузке в вышеприведённых формулах принимаются _f1=_f2=_f=1,0; динамический коэффициент 1+=1,0:

М₁= = =5968,11 кНм;

М₂= = =7520,97 кНм;

Q₀= = =2035,36 кН;

Q₂= = =1434,99 кН.

Огибающие эпюры представлены на рис. 4.

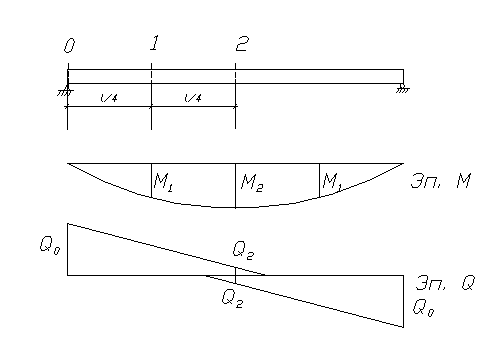
Рис.4. Огибающие эпюры в разрезной балке.

Расчёт балки из обычного железобетона.

Расчёт на прочность по изгибающему моменту.

Расчёту подлежат балочные пролётные строения железнодорожных мостов из обычного железобетона ( типовой проект серии 3.501-108).

Действительную форму поперечного сечения приводим к расчётной форме (рис. 5).

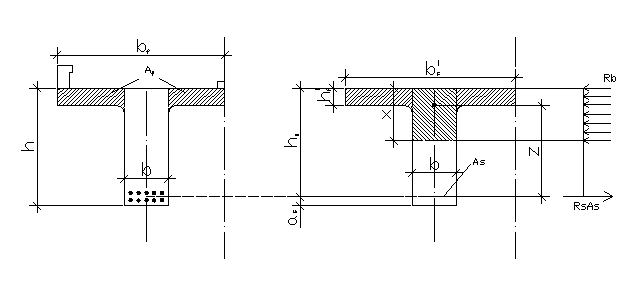
Рис. 5. Расчётная схема поперечного сечения главной балки.

Вычисляем приведённую (среднюю) толщину плиты при фактической ширине плиты b_f=2,09 м:

h_f^’= = =0,26 м.

Максимальная ширина плиты сжатой зоны тавровых и коробчатых сечений, учитываемая в расчёте, ограничена длиной свесов плиты, которая не должна быть больше 6h_f=1,56 м ; расчётная ширина плиты b_f^’ таврового сечения не должна превышать значения b_f^’ b+12h_f^’=3,62 м, а длина свесов плиты между соседними балками не должна быть больше 0,5(B-b)=0,5(1,80-0,50)=0,65 м, где B=1,80 м- расстояние между осями главных балок.

Действительная форма плиты переменной толщины и вутов заменяется в расчётном сечении прямоугольной формой с толщиной h_f^’ и шириной b_f^’.

Центр тяжести арматуры ориентировочно назначается на расстоянии a_s=0,16 м от нижней грани пояса балки.

Расчёт на прочность по изгибающему моменту производим, начиная с наиболее нагруженного сечения. Определим в первом приближении высоту сжатой зоны бетона x₁ при действии расчётного момента М₂=11318,71 кН/м:

x₁=h₀- =1,24- =0,3241 м.

Получаем x₁=0,3241 м >h_f^’=0,26 м , то из этого следует, что в сжатую зону, кроме плиты входит часть ребра главной балки, и сечение рассчитывается как тавровое. Расчетный изгибающий момент М₂ можно представить как сумму двух моментов: М₂`- воспринимаемый свесами плиты, М₂`` - воспринимаемый сжатой зоной ребра.

М₂= М₂`+ М₂``

Предельный момент, воспринимаемый свесами плит и соответствующей частью рабочей арматуры, равен:

М₂`= =15,5*1000*(2,09-0,5)*0,26*(1,24-0,5*0,26)=7112,55 кН

По оставшейся части момента

М₂``= М₂- М₂`=11318,71-7112,55=4206,16 кН

Находим высоту сжатой зоны в ребре:

x₁=h₀- =1,24- =0,5676 м.

Плечо пары внутренних сил таврового сечения

z=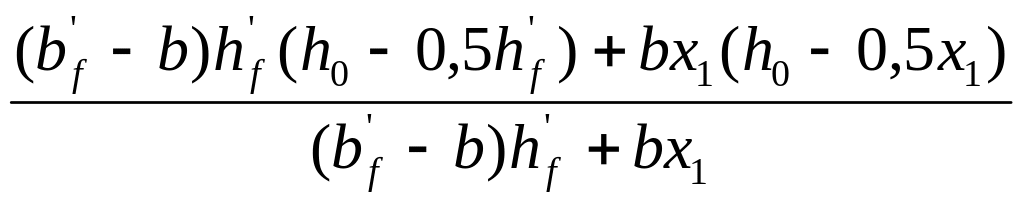 = =1,047 м.

Определяем необходимая площадь рабочей арматуры

.

Армирование будем производить пучками арматурой класса А-III диаметром d=40мм. Площадь поперечного сечения одного стержня равна 8,04 см². Определяем необходимое количество стержней:

n_ст = =26,06 шт.

Принимаем количество стержней n_ст=27.

После уточнения площади A_s c учётом принятого количества стержней арматуры находим значение x₂:

x₂= = =0,6184 м.

Окончательное значение z вычисляем по формуле:

z=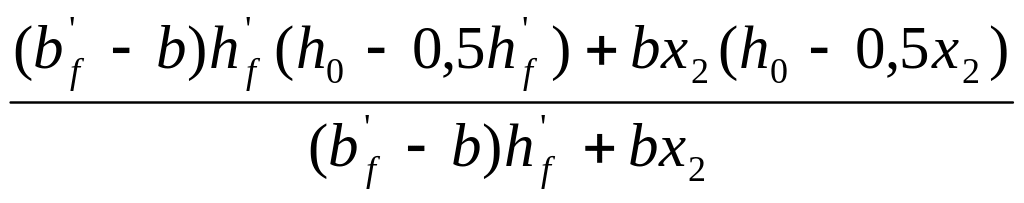 = =1,0333 м.

Условие прочности сечения по изгибающему моменту записывается в виде

М_пр=R_sA_szМ₂

М_пр=330000*339,39*10^-4*1,0333=11573,05 кН М₂=11318,71 кН.

Проверка выполняется, расчёт сечения на прочность по изгибающему моменту закончен.

Расчёт на трещиностойкость по касательным напряжениям.

Расчёт по касательным напряжениям выполняем в предположении упругой работы конструкции, но без учёта бетона растянутой зоны. В расчёте ограничивается величина касательных напряжений, действующих по нейтральной оси сечения.

Касательные напряжения могут быть определены по формуле:

;

где - поперечная сила в рассматриваемом сечении;

b - толщина ребра балки;

z - плечо пары внутренних сил из расчёта на прочность по изгибающему моменту.

При переменной толщине ребра балки из условия определяем толщины b₁ и b₂ в опорном сечении и в середине пролёта:

.

=0,5693 м=56,93см; принимаем b₁=57 см;

=0,4014 м=40,14 см; принимаем b₂=41 см.

Максимальная поперечная сила, воспринимаемая при меньшей толщине ребра b₂:

=1465,80 кН.

Расстояние от места изменения толщины до середины пролёта будет равно

м.

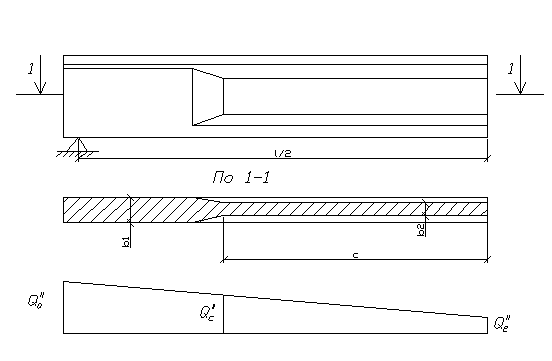
Рис. 6. Схема к расчёту на трещиностойкость по касательным напряжениям.

Расчёт на прочность по поперечной силе.

Поперечная сила в наклонном сечении воспринимается отогнутой арматурой, хомутами и бетоном сжатой зоны.

Места отгибов стержней рабочей арматуры согласуем с эпюрой действующих в балке изгибающих моментов.

Предельный момент, воспринимаемый сечением с одним стержнем рабочей арматуры равен

.

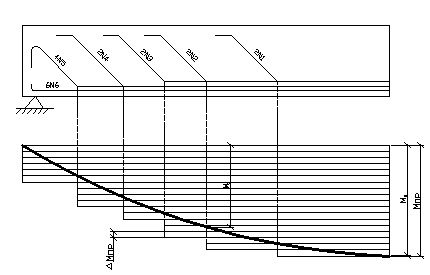
Рис.7. Схема к расчёту главной балки.

Угол наклона стержней к оси балки α=45˚. Не менее 1/3 стержней рабочей арматуры доводим без отгибов до опоры ( см. рис.7).

Проверка прочности наклонного сечения (рис.8.) на действие поперечной силы производится из условия:

;

где Q - максимальное значение поперечной силы от внешних нагрузок;

R_sw=0,8R_s - расчётное сопротивление арматуры отогнутых стержней и хомутов;

A_si и A_sw - площади поперечного сечения соответственно одного отогнутого стержня и всех ветвей хомута, пересекающего наклонное сечение;

- поперечное усилие, передаваемое на бетон сжатой зоны сечения;

с - длина горизонтальной проекции сечения.

Проверка наклонного сечения у опоры.

На приопорных участках длиной 2h₀ наклонное сечение составляет с продольной осью балки угол 45˚, длина его горизонтальной проекции равна с=h₀-x=1,24-0,11=1,13 м.

Располагая схемой размещения отогнутых стержней ( рис.8), определяем количество стержней, пересекающих наклонное сечение и их суммарную площадь .

Площадь всех ветвей одного хомута определяется из выражения:

=2,26 см²;

где d_sw - диаметр хомутов;

n - число ветвей одного хомута.

Шаг хомутов на концевых участках принимаем a_sw=10см, в середине пролёта - a_sw=15см.

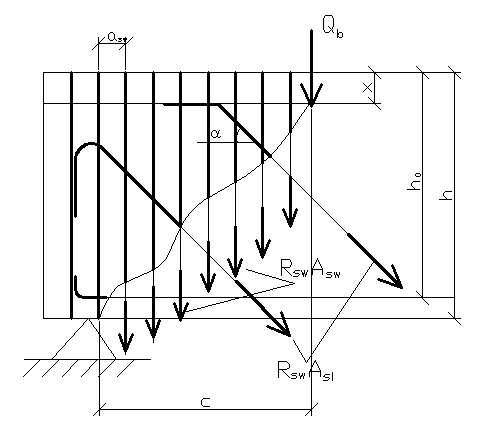Рис. 8. Схема к расчёту наклонного сечения у опоры.

Производим проверку:

;

, проверка выполняется, прочность приопорного участка обеспечена!

Проверка наклонного сечения в середине пролёта.

В середине пролёта прочность наклонного сечения обеспечивается постановкой хомутов с шагом 15 см. Длина проекции наклонного сечения равна 2h₀=2,48 м. Количество хомутов, пересекающих наклонное сечение, равно 16. Проводим проверку наклонного сечения:

, проверка выполняется, прочность сечения в середине пролёта обеспечена!