17. Формула Ньютона-Лейбница.

18. Замена переменной в определенном интеграле.

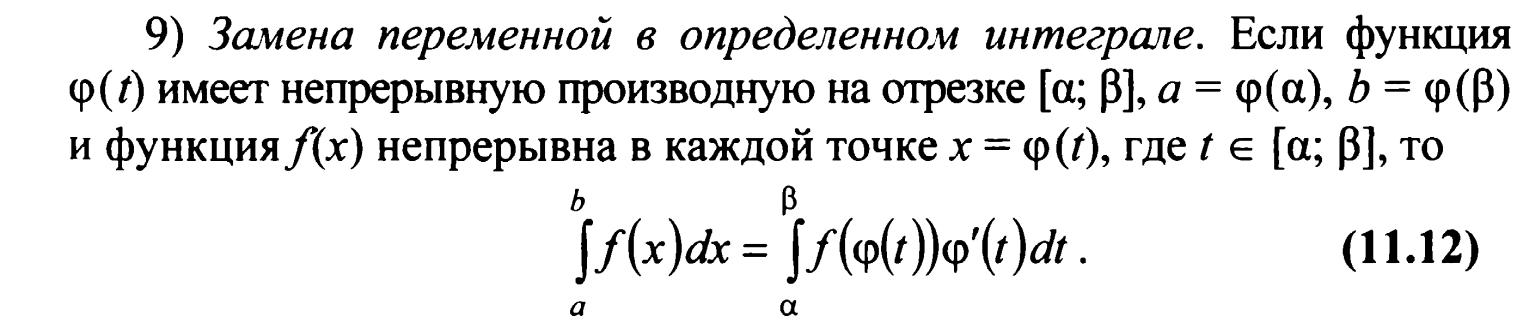
19. Интегрирование по частям в определенном интеграле.

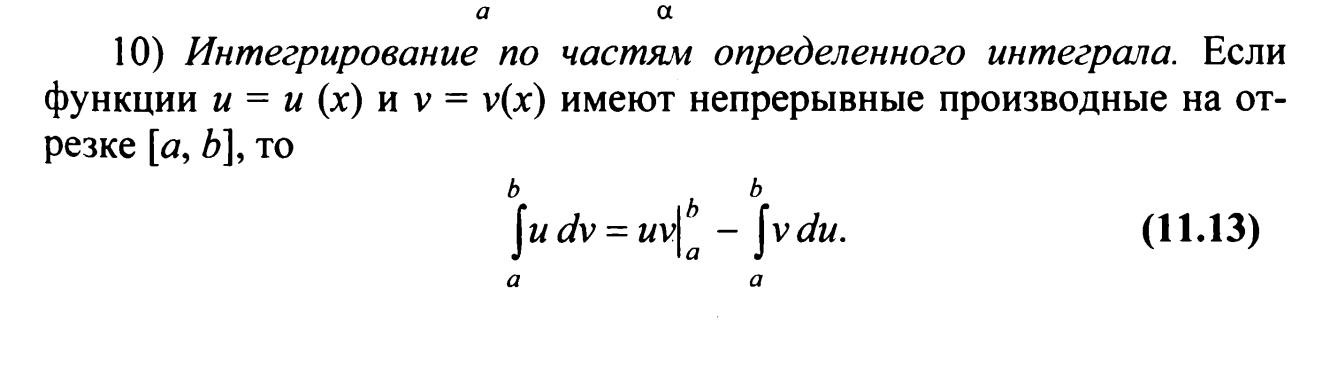20 Геометрические приложения определенного интеграла

.1. Вычисление площадей плоских фигур.

у

+ +

0 a - b x

Известно, что определенный интеграл на отрезке представляет собой площадь криволинейной трапеции, ограниченной графиком функции f(x). Если график расположен ниже оси Ох, т.е. f(x) < 0, то площадь имеет знак “-“, если график расположен выше оси Ох, т.е. f(x) > 0, то площадь имеет знак “+”.

Для нахождения суммарной площади используется формула .

Площадь фигуры, ограниченной некоторыми линиями может быть найдена с помощью определенных интегралов, если известны уравнения этих линий.

2. Нахождение площади криволинейного сектора.

 = f()



О  

Для нахождения площади криволинейного сектора введем полярную систему координат. Уравнение кривой, ограничивающей сектор в этой системе координат, имеет вид  = f(), где  - длина радиус – вектора, соединяющего полюс с произвольной точкой кривой, а  - угол наклона этого радиус – вектора к полярной оси.

Площадь криволинейного сектора может быть найдена по формуле

.3. Вычисление длины дуги кривой.

y y = f(x)

S_i y_i

x_i

a b x

Длина ломаной линии, которая соответствует дуге, может быть найдена как

4. Вычисление объемов тел.

Вычисление объема тела по известным площадям его параллельных сечений.

Q(x_i-1)

Q(x_i)

a x_i-1 x_i b x

Если функция y=y(x) на отрезке ( a,b), то объем

тела, образованного вращением вокруг оси Оx

фигуры, ограниченного линиями y=y(x), x=a,x=b.

y=0 вычисляется по формуле:

Аналогично, объем ,образованного при вращении вокруг оси Oy плоской фигуры, ограниченной линиями y=c, y=d, x=x(y), x=0, вычисляется по формуле:

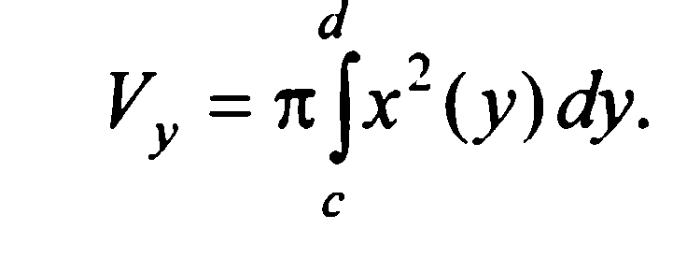
21Понятие дифференциального уравнения. Задача Коши.

Задача Коши – это задача нахождения

частного решения дифференциального

уравнения, удовлетворяющего заданным начальным условиям , где - числа.