1. Определение функции двух

и более переменных.

Определение 1.1. Переменная z (с областью изменения Z) называется функцией двух независимых переменных х,у в множестве М, если каждой паре (х,у) из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z.

Определение 1.2. Множество М, в котором заданы переменные х,у, называется областью определения функции, а сами х,у – ее аргументами.

Обозначения: z = f(x,y), z = z(x,y).

Примеры.

z = xy, z = x² + y² - функции, определенные для любых действительных значений х,у.

- функция, областью определения которой являются решения неравенства .

 Замечание. Так как пару чисел (х,у) можно считать координатами некоторой точки на плоскости, будем впоследствии использовать термин «точка» для пары аргументов функции двух переменных, а также для упорядоченного набора чисел , являющихся аргументами функции нескольких переменных.

 Определение 1.3. . Переменная z (с областью изменения Z) называется функцией нескольких независимых переменных в множестве М, если каждому набору чисел из множества М по некоторому правилу или закону ставится в соответствие одно определенное значение z из Z. Понятия аргументов и области определения вводятся так же, как для функции двух переменных.

Обозначения: z = f , z = z .

3. График функции двух переменных. Линии уровня. Поверхности уровня.

Геометрическое изображение функции двух переменных.

 

Рассмотрим функцию z = f(x,y), (1.1)

определенную в некоторой области М на плоскости Оху. Тогда множество точек трехмерного пространства с координатами (x,y,z), где , является графиком функции двух переменных. Поскольку уравнение (1.1) определяет некоторую поверхность в трехмерном пространстве, она и будет геометрическим изображением рассматриваемой функции.

\

Примерами могут служить изучаемые в предыдущем семестре уравнения плоскости

z = ax + by + c

и поверхностей второго порядка:

z = x² + y² (параболоид вращения),

(конус) и т.д.

Замечание. Для функции трех и более переменных будем пользоваться термином «поверхность в n-мерном пространстве», хотя изобразить подобную поверхность невозможно.

 

Линии и поверхности уровня. Для функции двух переменных, заданной уравнением (1.1), можно рассмотреть множество точек (х,у) плоскости Оху, для которых z принимает одно и то же постоянное значение, то есть z = const. Эти точки образуют на плоскости линию, называемую линией уровня.Пример.

Найдем линии уровня для поверхности z = 4 – x² - y². Их уравнения имеют вид x² + y² = 4 – c (c=const) – уравнения концентрических окружностей с центром в начале координат и с радиусами . Например, при с=0 получаем окружность x² + y² = 4 .Для функции трех переменных u = u (x, y, z) уравнение u (x, y, z) = c определяет поверхность в трехмерном пространстве, которую называют поверхностью уровня.Пример.Для функции u = 3x + 5y – 7z –12 поверхностями уровня будет семейство параллельных плоскостей, задаваемых уравнениями 3x + 5y – 7z –12 + с = 0.

 4. Предел и непрерывность функции нескольких переменных.

Предел функции нескольких переменных.

Определение: Окрестностью точки М₀(х₀, у₀) радиуса r называется совокупность всех точек (х, у), которые удовлетворяют условию .

Определение: Число А называется пределом функции f(x, y) при стремлении точки М(х, у) к точке М₀(х₀, у₀), если для каждого числа  > 0 найдется такое число r >0, что для любой точки М(х, у), для которых верно условие

также верно и условие .

Записывают:

19.3. Непрерывность функции нескольких переменных.

Определение: Пусть точка М₀(х₀, у₀) принадлежит области определения функции f(x, y). Тогда функция z = f(x, y) называется непрерывной в точке М₀(х₀, у₀), если

(1)

причем точка М(х, у) стремится к точке М₀(х₀, у₀) произвольным образом.

Если в какой – либо точке условие (1) не выполняется, то эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях:

Функция z = f(x, y) не определена в точке М₀(х₀, у₀).

Не существует предел .

Этот предел существует, но он не равен f( x₀, y₀).

 5. Определение частных производных

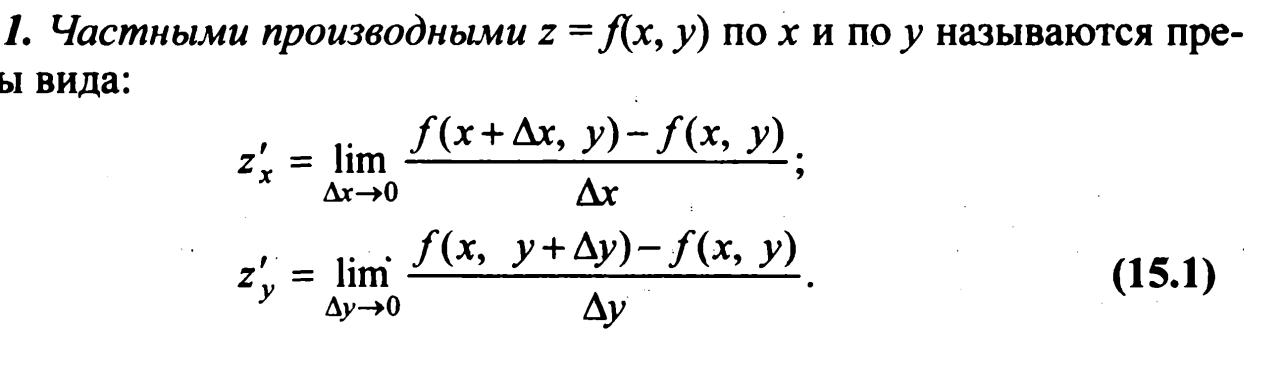Из определения частной производной следует правило: при вычислении производной по одной из переменных все остальные переменные считаем постоянными, учитывая, что производная постоянной равна нулю и постоянную можно выносить за знак производной.

6. Определение смешенных производных.

Рассматривая.я частные производные и 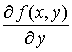как функции от , приходим к понятиям частных производных второго порядка. А именно, выражения

,

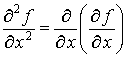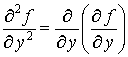
называют частными производными второго порядка функции по и по соответственно, а выражения

,

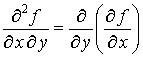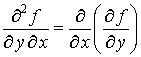
– смешанными частными производными второго порядка функции . Их обозначают также символам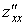и: , , и . Аналогично определяют частные производные 3-го порядка (их будет 8=2³ ), 4-го порядка (их будет 16=2⁴ ) и т.д.

7. Дифференциал функции нескольких переменных.

8. Экстремум функции нескольких переменных.

Экстремум функции нескольких переменных.

Необходимое и достаточное условие экстремума.

Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

то точка М₀ называется точкой максимума.

Определение. Если для функции z = f(x, y), определенной в некоторой области, в некоторой окрестности точки М₀(х₀, у₀) верно неравенство

то точка М₀ называется точкой минимума.

Теорема. (Необходимые условия экстремума).

Если функция f(x,y) в точке (х₀, у₀) имеет экстремум, то в этой точке либо обе ее частные производные первого порядка равны нулю , либо хотя бы одна из них не существует.

Эту точку (х₀, у₀) будем называть критической точкой.

Теорема. (Достаточные условия экстремума).

Пусть в окрестности критической точки (х₀, у₀) функция f(x, y) имеет непрерывные частные производные до второго порядка включительно. Рассмотрим выражение:

Если D(x₀, y₀) > 0, то в точке (х₀, у₀) функция f(x, y) имеет экстремум, если

- максимум, если - минимум.

Если D(x₀, y₀) < 0, то в точке (х₀, у₀) функция f(x, y) не имеет экстремума

В случае, если D = 0, вывод о наличии экстремума сделать нельзя.

Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение

g(х, у) = 0, которое называется уравнением связи

Точка условного экстремума явл точкой экстремума функ-ции

L(x,y, ) = f(x, y) + (x, y). Функция L называется функцией Лагранжа.

- называется множителем Лагранжа

При исследовании функц-и на экстремум рекомендуется пользоваться след схемой:

1) найти частные производные

2) решить систему уравнений и найти критические точки

3) найти частные производные второго порядка, вычислить их значения в каждой критич точке и с помощью достаточного условия сделать вывод о наличии экстремумов

4) найти экстремумы(экстрем значения) функ-и

9. Необходимые и достаточные условия экстремума функции нескольких (двух) переменных

Рассмотрим функцию , где -- открытое множество.

Определение 1.   называется точкой максимума (минимума) функции , если

Аналогично если выполняется строгое неравенство, точка называется точкой строгого максимума (строгого минимума).

Теорема 1. (необходимое условие экстремума)   Если -- точка экстремума и существует , то .

Теорема 2. (достаточное условие экстремума)   Если дважды дифференцируема в стационарной точке , то -- точка минимума (максимума), если квадратичная форма положительно (отрицательно) определена. Если эта форма не определена, то экстремума в этой точке нет. Если она вырождена, то неизвестно, является ли точкой экстремума.

10. Понятия первообразной функции и неопределенного интеграла.

Первообразная функция.

Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:

F(x) = f(x).

Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.

F₁(x) = F₂(x) + C.

Неопределенный интеграл.

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

F(x) + C.

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.