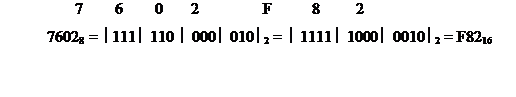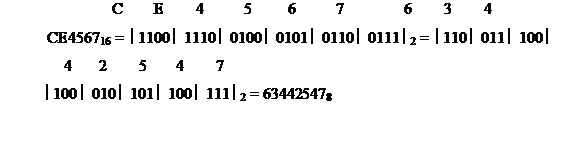2.2.5 Работа с числами в других системах счисления, используемых

в компьютерных технологиях

Восьмеричная и шестнадцатеричная системы счисления являются вспомогательными системами при подготовке задачи к решению. Удобство ее использования состоит в том, что числа соответственно в 3 и 4 раза короче двоичной системы, а перевод в двоичную систему и обратно несложен и выполняется простым механическим способом.

Для того чтобы произвольное двоичное число записать в системе счисления с основанием q =2ⁿ , нужно:

­        данное двоичное число разбить слева и справа (целую и дробную части) на группы по  n цифр в каждой;

­ если в последних правой и левой группах окажется меньше n разрядов, то их надо дополнить справа и слева нулями до нужного числа разрядов;

­  рассмотреть каждую группу как n – разрядное двоичное число и записать ее соответствующей цифрой в системе счисления с основанием   q = 2ⁿ.

Значит для того чтобы произвольное число записать в системе счисления с основанием q = 2ⁿ , т. е. перевести в двоичную систему счисления, нужно каждую цифру этого числа заменить ее n-разрядным эквивалентом в двоичной системе счисления. Применительно к компьютерной информации часто используются системы счисления с основанием 8 (восьмеричная) и 16 (шестнадцатеричная).

Перевод из двоичной в восьмеричную и шестнадцатеричную систему счисления и обратно. Для того чтобы двоичное число записать в восьмеричной системе счисления, необходимо разбить его на триады (т.е. группы по 3 цифры, так как 8 = 2³), начиная от запятой, отделяющей целую часть от дробной части. После этого каждая триада заменяется одной соответствующей ей восьмеричной цифрой. Недостающие справа и слева цифры восполняются нулями. Связь между двоичной и восьмеричной системами счисления  приведена в таблице 2.2. Каждой восьмеричной цифре соответствует тройка – тетрада двоичных чисел.

Таблица 2.2 – Двоично-восьмеричная таблица

 

8-я система счисления	2-я система счисления
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

 

Пример 17. Перевести число 1011101,10111₂ в восьмеричную систему счисления.

1011101,10111₂ =  001  011  101 ,  101  110   = 135,56₈   

 

Перевод двоичных чисел в шестнадцатеричную систему счисления. Для того чтобы двоичное число записать в 16-ричной системе счисления, необходимо разбить его на тетрады (группы из 4 цифр, т.к. 16 = 2⁴), начиная от запятой, в обе стороны. После этого каждая тетрада заменяется соответствующей ей 16-ричной цифрой. В этом случае используется двоично-шестнадцатеричная таблица. Связь между двоичной и шестнадцатеричной системами счисления приведена  в таблице 2.3.

Таблица 2.3 – Двоично-шестнадцатеричная таблица.

 

16-я система счисления	2-я система счисления		16-я система счисления	2-я система счисления
0	0000		8	1000
1	0001		9	1001
2	0010		A	1010
3	0011		B	1011
4	0100		C	1100
5	0101		D	1101
6	0110		E	1110
7	0111		F	1111

 

Пример 18. Перевести число 1011101,10111₂ в шестнадцатеричную систему счисления.

1011101,10111₂ =   0101   1101 ,  1011  1000  = 5D,B8₁₆

Перевод восьмеричных и шестнадцатеричных чисел в двоичную систему счисления. Для перевода 8-ричного числа в двоичную систему счисления достаточно каждую восьмеричную цифру нужно заменить соответствующей ей двоичной триадой. Для перевода 16-го числа в двоичную систему  счисления достаточно каждую шестнадцатеричную цифру заменить соответствующей ей двоичной тетрадой.

 

Пример 19. Перевести числа в двоичную систему.

 

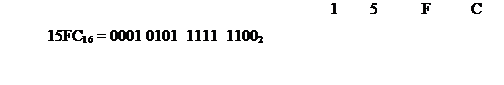
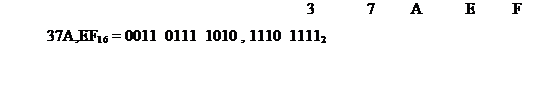
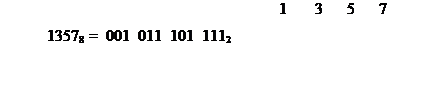
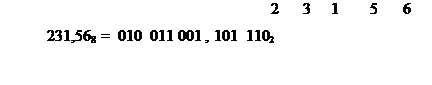
При переходе из 8-ричного счисления в 16-ричное счисление и обратно используется вспомогательный, двоичный код числа.

 

Пример 20. Перевести восьмеричные числа в шестнадцатеричные и наоборот шестнадцатеричные числа в восьмеричные.