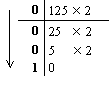2.2.3 Арифметические действия над двоичными числами

В компьютерах для записи чисел используется двоичная система счисления.  В этой системе для представления любого числа используются два символа — цифры  0 и 1. Основание системы счисления 

Произвольное число с помощью формулы можно представить в виде разложения по степеням двойки:

(2.8)

 

Таким образом, все числа в двоичной системе счисления составляются из цифр 0 или 1. Например, x = (110011,1101)₂. Двоичное представление числа требует примерно в 3,3 раза большего числа разрядов, чем его десятичное представление. Тем не менее, применение двоичной системы счисления создает большие удобства для работы ЭВМ, так как для представления в машине разряда двоичного числа может быть использован любой запоминающий элемент, имеющий два устойчивых состояния.

Арифметические действия над одноразрядными двоичными числами выполняются по следующим правилам:

 

		(2.9)

 

При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и перенос единицы из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.

 

Пример 7. Выполнить сложение двоичных чисел:

а) X=1101, Y=101;

    

Результат 1101+101=10010.

б) X=1101, Y=101, Z=111;

    

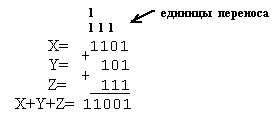
Результат 1101+101+111=11001.

 

При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.

 

Пример 8. Заданы двоичные числа X=10010 и Y=101. Вычислить X-Y.

    

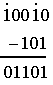
Результат 10010 - 101=1101.

Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.

 

Пример 9. 1001 101=?

    

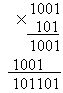
Результат 1001 101=101101.

 

Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.

Пример 10.   1100.011 : 10.01=?

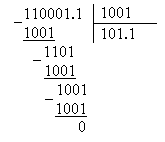Результат 1100.011 : 10.01=101.1.

 

2.2.4. Перевод чисел в различные позиционные системы счисления

ЭВМ работают с двоичными кодами, пользователю удобнее иметь дело с десятичными или шестнадцатеричными кодами. Возникает необходимость перевода числа из одной системы счисления в другую. Любое число по специальным правилам можно перевести из одной системы счисления в другую. Рассмотрим эти правила.

Допустим, число Х из системы счисления с основанием q требуется перевести в систему счисления с основанием p. Числа, имеющие целую и дробные части, переводятся в два этапа: вначале целая часть числа, а затем дробная.

Перевод целых чисел из одной системы счисления в другую осуществляется по следующему правилу:

-          целую часть числа делим на новое основание p;

-          полученный от деления первый остаток является младшей цифрой целой части числа с основанием  р;

-          деление будем производить до тех пор, пока не получим частное меньше делителя;

-          последнее частное дает старшую цифру числа с основанием р

Перевод дробных чисел из одной системы счисления в другую. Предположим, что правильную дробь Х, представленную в системе с основанием q, требуется перевести в систему счисления с основанием р. Перевод осуществляется по следующему правилу:

-                     исходное число умножаем на новое основание р;

-                     полученная при этом целая часть произведения является первой искомой цифрой;

-                     дробную часть снова умножаем на основание р и т.д.

Перевод чисел в десятичную систему осуществляется путем составления степенного ряда с основанием той системы, из которой число переводится по формуле (2.6). Затем подсчитывается значение суммы.

 

Пример 11.

а) Перевести 10101101.101₂ в 10-ю систему счисления

Замечание: Здесь и в дальнейшем при одновременном использовании нескольких различных систем счисления основание системы счисления, к которой относится число, будем указывать в виде нижнего индекса.

10101101.101₂ = 1 2⁷+ 0 2⁶+ 1 2⁵+ 0 2⁴+ 1 2³+ 1 2²+ 0 2¹+ 1 2⁰+ 1 2^-1+ 0 2^-2+ 1 2^-3 =  173.625₁₀

б) Перевести 703.04₈ в 10-ю систему счисления

703.04₈ = 7∙8²+ 0∙8¹+ 3∙8⁰+ 0 8^-1+ 4∙8^-2 = 451.0625₁₀

в) Перевести B2E.4₁₆ в 10-ю систему счисления

B2E.4₁₆ =  11∙16²+ 2∙16¹+ 14∙16⁰+ 4∙16^-1 = 2862.25₁₀

Перевод целых десятичных чисел в недесятичную систему. Допустим, число A из системы счисления с основанием q требуется перевести в систему счисления с основанием 2 или систему счисления с другим основанием.

 При переводе целой части числа из десятичной системы счисления в двоичную систему счисления применяется метод последовательного деления на число 2, равное основанию новой системы счисления. Полученное частное сравнивается с делителем. Если частное больше делителя, то теперь уже частное делим на основание системы. И так до тех пор, пока частное не станет меньше делителя 2. Результат формируется путем последовательной записи последнего частного и всех без исключения остатков деления, начиная с последнего.

Для перевода числа из системы счисления с основанием 2 в десятичную, следует сложить все степени с основанием 2, соответствующие позициям разрядов исходного 2-го числа, в которых цифры равны 1.

 

Пример 12. Перевести 165₁₀ в 2-ю систему счисления

165	2
-164	82	2
1	-82	41	2
	0	-40	20	2
		1	-20	10	2
			0	-10	5	2
				0	-4	2	2
					1	-2	1
						0

 

Результат: 165₁₀ = 10100101₂

Аналогичная операция производится при переводе числа в систему счисления с другим основанием.

 

Пример 13.

а) Перевести 181₁₀ в 8-ю систему счисления

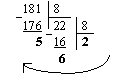    Результат: 181₁₀ = 265₈

б) Перевести 622₁₀ в 16-ю систему счисления

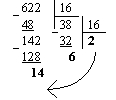    Результат: 622₁₀ = 26E₁₆

 

Перевод правильных дробей из десятичной системы счисления в недесятичную. При переводе дробной части числа применяется метод последовательного умножения на число, равное основанию новой системы счисления.

Перевод осуществляется по следующему правилу:

-                     исходное число умножаем на новое основание 2;

-                     полученная при этом целая часть произведения является первой искомой цифрой;

-                     дробную часть снова умножаем на основание 2 т.д.

Результат формируется путем последовательной записи целых частей произведения, начиная с первого.

 

Пример 14.

Перевести 0.3125₁₀ в 8-ю систему счисления

    

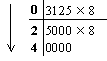
Результат: 0.3125₁₀ = 0.24₈

Замечание: Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.

 

Пример 15.

Перевести 0.65₁₀ в 2-ю систему счисления с точностью 6 знаков.

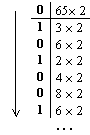     Результат: 0.65₁₀   0.10(1001)₂

Перевод неправильной десятичной дроби в систему счисления с недесятичным основанием. Перевод смешанных чисел, содержащих целую и дробную части, осуществляется в два этапа. Целая и дробная части исходного числа переводятся отдельно по соответствующим алгоритмам. В итоговой записи числа в новой системе счисления целая часть отделяется от дробной запятой  (точкой).

 

Пример 16.

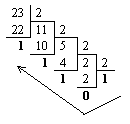
Перевести 23.125₁₀  в 2-ю систему счисления

1) Переведем целую часть:	2) Переведем дробную часть:

 

 

 

 

 

 

 

Таким образом:  23₁₀ = 10111₂; 0.125₁₀ = 0.001₂.

Результат:  23.125₁₀ = 10111.001₂.

Необходимо отметить, что целые числа остаются целыми, а правильные дроби – дробями в любой системе счисления.