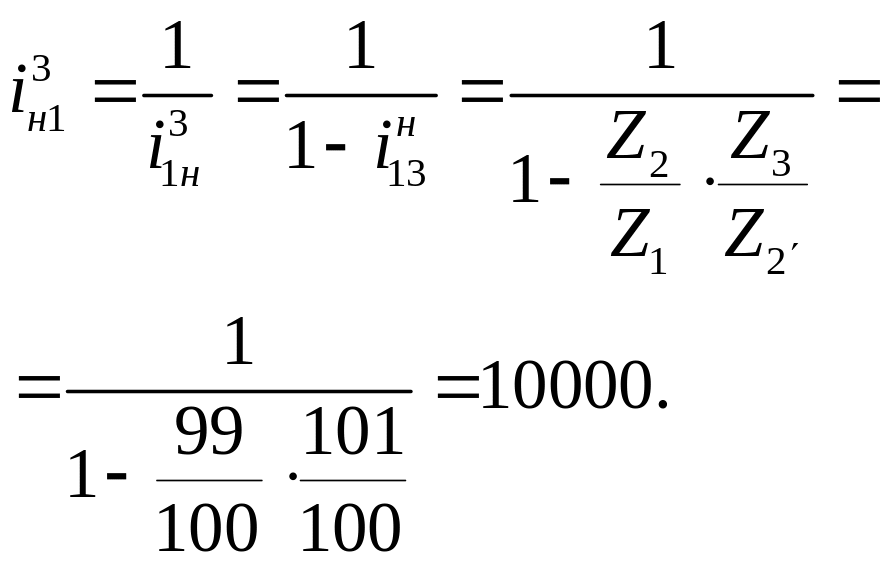- •Тема 1. Структура механизмов
- •19. Основные понятия
- •20. Классификация кинематических пар. Кинематические цепи
- •21 Кинематические цепи
- •22. Конструктивно-функциональная классификация механизмов
- •23. Структурные формулы механизмов
- •24. Структурный синтез и анализ механизмов
- •25. Общие сведения о передачах. Основные виды зубчатых передач
- •26 Элементы зубчатого колеса
- •27 Теорема виллиса
- •28. Общие сведения о методах изготовления зубчатых колес
- •29. Кинематика зубчатых механизмов с неподвижными осями вращения
- •(12.13)30,31. Кинематика зубчатых механизмов с подвижными осями вращения
(12.13)30,31. Кинематика зубчатых механизмов с подвижными осями вращения
Механизмы, в составе которых имеется хотя бы одно колесо с перемещающейся в пространстве осью вращения, называются планетарными. Различают три вида таких механизмов: 1)простые, 2)дифференциальные, 3) замкнутые дифференциальные.
Рассмотрим один из простейших дифференциальных механизмов (рис.2.10).Звенья 1 и 3 – центральные колеса, 2 – сателлит, Н –водило. Водило Н и соосные с ним центральные колеса 1 и 3 называются основными звеньями.
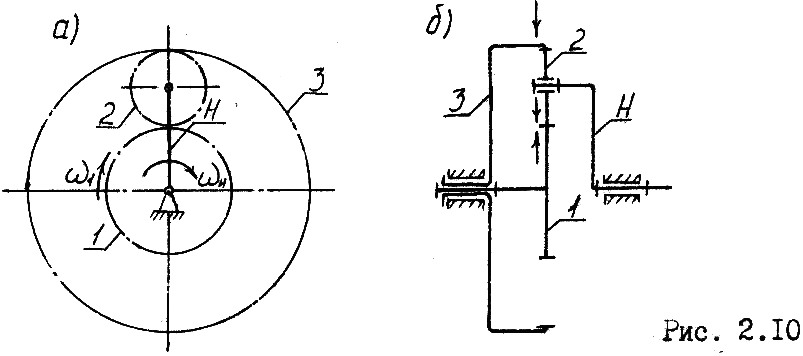
Получим
формулу, связывающую угловые скорости
звеньев в дифференциальном механизме.
Используем метод обращения движения.
Сообщаем всем звеньям механизма
дополнительную угловую скорость, равную
угловой скорости водила Н, но противоположно
направленную, т.е. (![]() ).
При этом относительное движение звеньев
не изменится, а угловые скорости в
обращенном движении будут следующими:
).
При этом относительное движение звеньев
не изменится, а угловые скорости в
обращенном движении будут следующими:
![]()
Таким
образом, так как
![]() то
дифференциальный механизм превратился
в зубчатый механизм с неподвижными
осями. Для такого обращенного механизма
то
дифференциальный механизм превратился
в зубчатый механизм с неподвижными
осями. Для такого обращенного механизма
![]() (2.6)
(2.6)
где
![]() -
передаточное
отношение обращенного механизма,
определяемое через число зубьев
колес:
-
передаточное
отношение обращенного механизма,
определяемое через число зубьев
колес:
![]()
Полученное выражение(2.6) называется формулой Виллиса. В общем случае формула Виллиса имеет вид
![]()
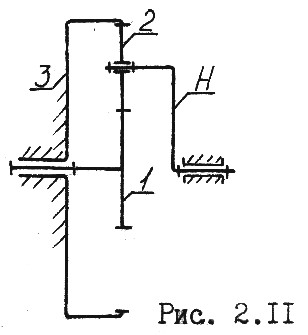
Если в дифференциальном механизме одно из центральных колес сделать неподвижным, то получится планетарный механизм (рис. 2.11).
Так
как
![]() то из формулы
то из формулы
![]() получим:
получим:
![]()
![]()
![]() (2.7)
(2.7)
Выражение(2.7) называется формулой Виллиса для планетарных механизмов. В общем случае она имеет вид
![]() (2.8)
(2.8)
где индекс в соответствует неподвижному центральному колесу.
Планетарные механизмы часто называются планетарными передачами. Они позволяют получать большие передаточные отношения при малых габаритах.
П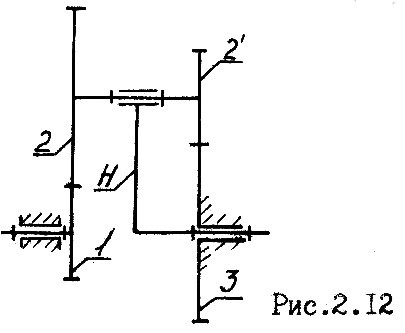 ример.
Определить
ример.
Определить
![]() если
если
![]()
![]()
![]() (рис.2.12).
(рис.2.12).
На основании формулы (2.7) находим