§25. Особые звенья

Эти звенья в отличие от типовых являются неминимально - фазовыми, т.е. при одной и той же АЧХ с соответствующим ему типовым звеном особое звено имеет ФЧХ с бóльшими по модулю ординатами. Математически это объясняется тем, что передаточные функции особых звеньев имеют нули и (или) полюсы, расположенные в правой комплексной полуплоскости. Особые звенья делятся на два вида:

1) с сосредоточенными в пространстве параметрами ;

2) с распределенными в пространстве параметрами .

Из особых звеньев с сосредоточенными параметрами в практике наиболее часто встречаются два:

1) Устойчивое неминимально-фазовое звено первого порядка.

2) Неустойчивое звено первого порядка.

Устойчивое неминимально-фазовое звено

Оно описывается дифференциальным уравнением первого порядка

,

которое отличается от уравнения инерционно-форсирующего звена разными знаками слагаемых правой части.

Передаточная функция имеет нуль , расположенный в правой полуплоскости.

Переходную функцию можно получить из функции инерционно-форсирующего звена изменением знака перед Т₂:

.

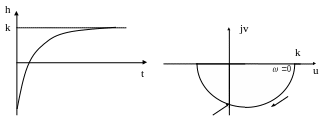Этой функции соответствует переходная характеристика в виде переходящей через ноль экспоненты.

Частотная передаточная функция :

показывает, что ее мнимая часть всегда отрицательна, и поэтому АФХ представляет собой полуокружность в нижней полуплоскости. ЛАХ у данного звена совпадает с ЛАХ инерционно- форсирующего звена первого порядка, так как изменение знака перед T­₂ не сказывается на модуле передаточной функции. ФЧХ определим из ЧПФ по правилу аргументов:

.

Эта формула показывает, что ФЧХ совпадает с ФЧХ апериодического звена второго порядка. Следовательно, данное звено является неминимально - фазовым по сравнению с инерционно - форсирующим звеном первого порядка.

Примером рассмотренного особого звена могут служить симметричные мостовые схемы с реактивными элементами.

R1>R2

Неустойчивое звено первого порядка

Его уравнение , п.ф .

Это уравнение отличается от уравнения инерционного звена первого порядка разными знаками слагаемых в левой части. Это звено называют так же квазиинерционным звеном первого порядка. Переходную функцию определим операторным методом: .

Применим формулу известной теоремы разложения. Если , то

, где , Q(s)=k

s_i -некратные корни уравнения D(s)=0. В данном случае -полюс передаточной функции,

Подставляя в формулу разложения, найдем .

Графиком этой функции является неограниченно возрастающая экспонента так же, как и для весовой функции

Весовая характеристика иллюстрирует свойства неустойчивости данного звена: после снятия приложенного воздействия в виде - функции выходная величина неограниченно удаляется от нулевого значения. Переходная характеристика имеет значения противоположного знака по сравнению с вынужденным (-k), которое из-за неустойчивости установившимся не является.

Частотная п.ф.

показывает, что АФХ расположена в третьем квадранте.

АЧХ совпадает с АЧХ инерционного звена первого порядка, а ФЧХ можно найти по правилу аргументов с учетом квадранта фазового угла. По модулю эта ФЧХ больше, чем у инерционного звена:

Примером может служить интегратор, охваченный положительной жесткой обратной связью, что видно из эквивалентной передаточной функции.

Особые звенья с распределенными параметрами

Эти звенья описываются дифференциальными уравнениями в частных производных:

- уравнение длинной линии;

- уравнение теплопроводности;

r - пространственная координата, изменяющаяся от 0 до ∞,

z - физическая переменная, характеризующая состояние звена.

В качестве выходной величины звена принимают y(t)=z( ,t), где - некоторое значение r.

В качестве входной могут выбираться разные величины:

Рассмотрим нахождение передаточной функции длинной линии при x(t)=z(0,t). Допустим, что в этом звене существует установившийся режим гармонических колебаний. При этом .

Для нахождения комплексной амплитуды подставим комплекс в уравнение длинной линии. После дифференцирования получим

.

Запишем соответствующее характеристическое уравнение, рассматривая r как независимую переменную:

.

Корни этого уравнения позволяют выразить комплексную амплитуду как функцию r следующей формулой:

.

Для звена направленного действия учитывается только прямая волна от входа к выходу и тогда

.

Соответствующая истинная функция времени и r определится обычным образом, т.е. как коэффициент при j:

и отсюда при r=0 и

,

,

где имеющее размерность времени произведение обозначается и называется временем запаздывания.

Определим частотную передаточную функцию как отношение комплексов выхода и входа

.

Заменив на s получим передаточную функцию в изображениях Лапласа

.

Эта передаточная функция трансцедентная.

Сравнение функций y(t) и x(t) позволяет записать уравнение данного звена в более простом виде:

.

Если в этом уравнении с запаздывающим аргументом правую и левую часть подвергнуть преобразованию Лапласа, получим такую же W(s). Согласно последнему уравнению, выходная величина звена в точности повторяет входную, но с постоянным запаздыванием . Поэтому звено называется звеном постоянного запаздывания и его переходная характеристика будет представлять собой единичную ступенчатую функцию, смещенную на :

, а .

Т.к. , то

АЧХ у данного звена такая же, как у безинерционного, а ФЧХ .

Следовательно, звено с постоянным запаздыванием является неминимально-фазовым по отношению к безинерционному звену.

Его АФХ представляет собой окружность единичного радиуса с центром в начале координат, которая с изменением  обходится периодически.

Примерами данного звена могут служить:

1

) Длинная линия без потерь, нагруженная на согласованное сопротивление Z_н при индуктивности L₀ и емкости C₀ на единицу длины l.

2) Транспортер сыпучих материалов.

x(t)-нагр.на 1м на входе

y(t)-нагр. на 1м на выходе

из бункера

V-скорость движения транспортной ленты.

v

l

Особые звенья, описываемые уравнением теплопроводности, имеют в качестве

переменной температуру, т.е. в некоторой точке объекта. Основные разновидности этих звеньев сведем в таблицу.

№	Название и п.ф	Вход	Выход	Пример
1	Звено полузапаздывания			Нагреваемый радиационным способом объект бесконечной толщины без учета теплоотвода с поверхности
2	Полуинтегрирущее	Удельная мощность излучения		То же
3	Полуинерционное 1-го рода	То же	То же	То же с учетом теплоотвода с поверхности
4	Полуинерционное 2-го рода	То же	То же	Объект радиационного или индукционного нагрева с осевой симметрией и с учетом теплоотвода.

Передаточные функция этих звеньев иррациональны(комплексная переменная s под корнем). Кроме того передаточная функция звена полузапаздывания еще и трансцедентна, что усложняет исследование систем с такими объектами. В этих случаях замена s на не имеет смысла.