
- •6.4 Режимы движения цапфы в подшипнике
- •6.5 Уравновешивание ротора
- •6.6 Статическая балансировка
- •6.7 Динамическая балансировка роторов
- •6.8 Допустимая неуравновешенность
- •7 Исследование кпм
- •7,1 1.Назначение и уст-во кпм.
- •7.2. Аналитический способ определения положения, скорости и ускорения ползуна
- •7,3 3.Индикаторная диаграмма и силы прилож. К ползуну
- •7,4. Момент инерции вращающегося звена и маховика
- •5.Степень неравномерности колеб. Кривошипа в кпм.
6.7 Динамическая балансировка роторов
На станках первой группы величины противовесов определяются непосредственно измерением динамических сил в опорах балансируемого ротора. На станках второй группы величины и положения противовесов находят с помощью компенсирующего устройства, установленного на станке, а третьей группы - колебанием подшипниковых опор балансируемого ротора.
Среди станков третьей группы широкое распространение получил станок, предложенный проф. Б.В. Шишковым. Принципиальная схема этого станка представлена на рис. 4.13.
Маятниковая рама 1, опираясь на пружину 2, может колебаться относительно горизонтальной оси, проходящей через точку О. Балансируемый ротор 3 устанавливается на опорах 4, жестко связанных с маятниковой рамой.
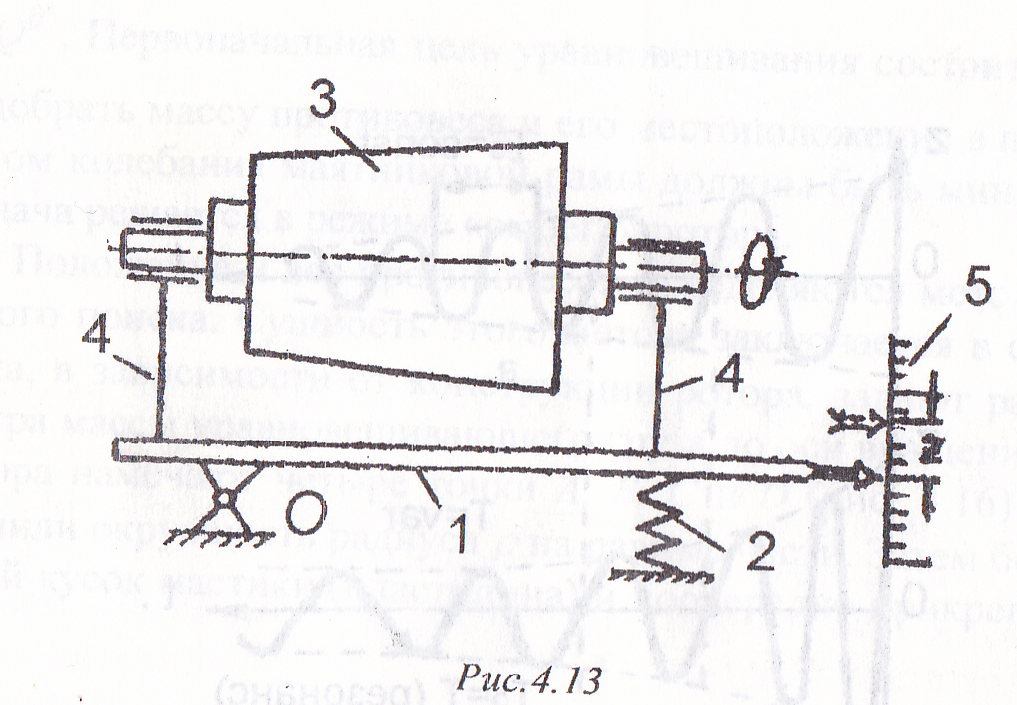 Ротор приводится во вращение с помощью
клиноременной передачи (на схеме не
показана). Кроме того, имеется отсчетное
устройство 5 для измерения амплитуды
колебаний маятниковой рамы.
Ротор приводится во вращение с помощью
клиноременной передачи (на схеме не
показана). Кроме того, имеется отсчетное
устройство 5 для измерения амплитуды
колебаний маятниковой рамы.
С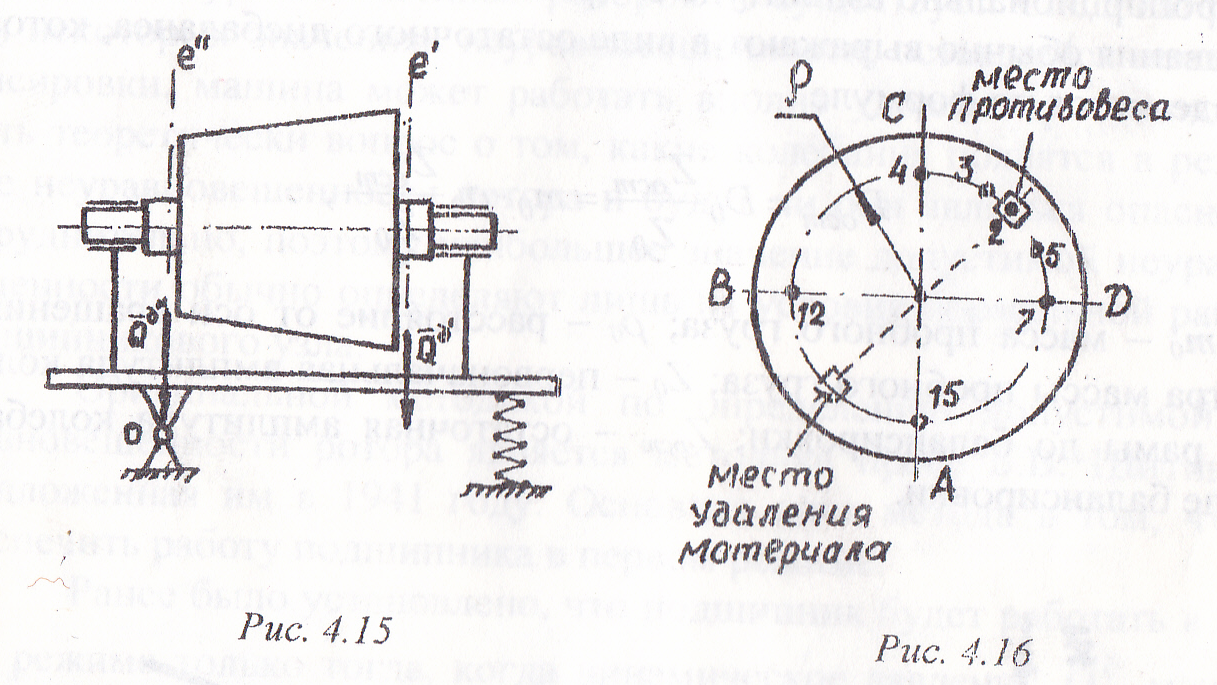 ущность
этого метода заключается в следующем.
Сначала, в зависимости от конструкции
ротора, задают расстояние р от центра
массы уравновешивающего груза до оси
вращения, и на торце ротора намечают
четыре точки А,
В, С и
D
(рис. 4.16) так, чтобы они делили окружность
радиуса р на равные части. Затем
берут произвольный кусок мастики
(пластилина) и поочередно прикрепляют
его в
ущность
этого метода заключается в следующем.
Сначала, в зависимости от конструкции
ротора, задают расстояние р от центра
массы уравновешивающего груза до оси
вращения, и на торце ротора намечают
четыре точки А,
В, С и
D
(рис. 4.16) так, чтобы они делили окружность
радиуса р на равные части. Затем
берут произвольный кусок мастики
(пластилина) и поочередно прикрепляют
его в
намеченных точках. Сообщая вращение ротору, замеряют амплитуды колебания при резонансе. Сопоставляя полученные значения, определяют сектор (CD) с наименьшими показателями амплитуд, который дополнительно делят на ряд точек, и повторяют вышеописанный процесс с мастикой той же массы, замеряя амплитуды колебания при ре зонансе во вновь отмеченных точках. Таким образом находят положение противовеса, местом которого является та точка, где амплитуда будет наименьшей.
На втором этапе ротор устанавливается так, чтобы плоскость е" не проходила через ось вращения маятниковой рамы, и по вышеописанной методике подпирается уравновешивающая масса груза и его положение в плоскости е".
Произведение массы противовеса или какого-либо другого груза ria расстояние центра масс до оси вращения называют дисбалансом:
D = тр.
П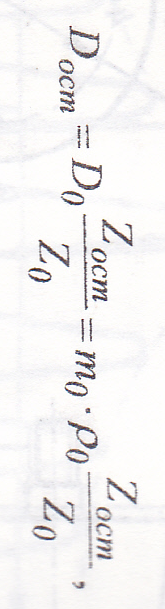 ри
этом массу груза измеряют в граммах, а
расстояние — в сантиметрах! Точность
уравновешивания обычно выражают в
виде остаточного дисбаланса, который
определяется по формуле
ри
этом массу груза измеряют в граммах, а
расстояние — в сантиметрах! Точность
уравновешивания обычно выражают в
виде остаточного дисбаланса, который
определяется по формуле
г де
mо - масса пробного груза;
ро - расстояние от оси вращения до центра
массы пробного груза;
Z0-
первоначальная амплитуда колебания
рамы до балансировки;
Zocm
—
остаточная амплитуда колебания после
балансировки. Остаточные дисбалансы
определяют отдельно для каждой плоскости
уравновешивания и сравнивают их с
допустимыми значениями. должно
выполняться условие: Dост<=Dдоп
де
mо - масса пробного груза;
ро - расстояние от оси вращения до центра
массы пробного груза;
Z0-
первоначальная амплитуда колебания
рамы до балансировки;
Zocm
—
остаточная амплитуда колебания после
балансировки. Остаточные дисбалансы
определяют отдельно для каждой плоскости
уравновешивания и сравнивают их с
допустимыми значениями. должно
выполняться условие: Dост<=Dдоп
6.8 Допустимая неуравновешенность
Ранее было установлено, что подшипник будет работать в первом режиме только тогда, когда динамическое давление QдA меньше статического QAс. Для надежности Б.В. Шитиков принял следующее соотношение:
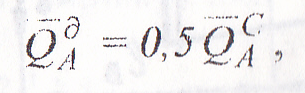
(4.4)
с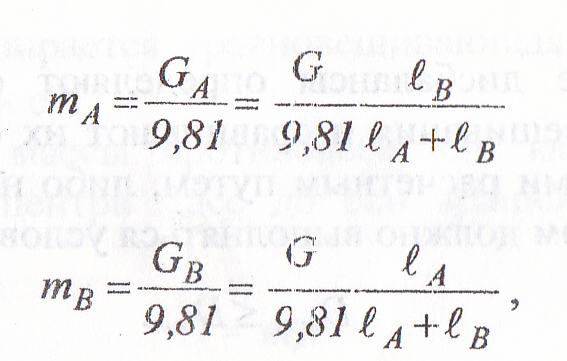
 огласно
которому вычисляется величина допустимого
смещения центра масс ротора от оси
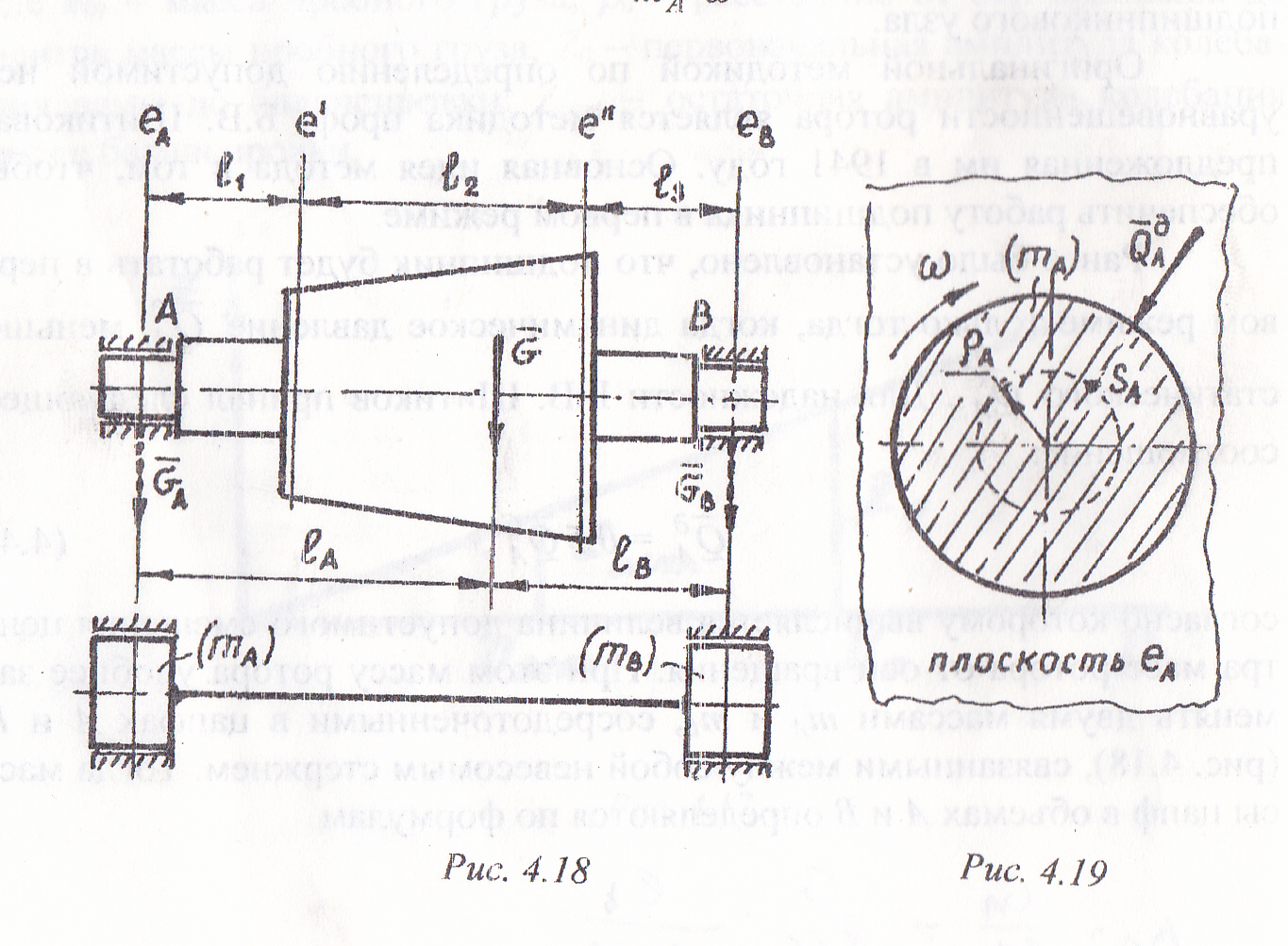
вращения ; При этом массу ротора удобнее
заменять двумя массами
тА
и mB,
сосредоточенными в цапфах
А и В (рис. 4.18), связанными между
собой невесомым стержнем. Тогда массы
цапф в объемах А и В определяются
по формулам
огласно
которому вычисляется величина допустимого
смещения центра масс ротора от оси
вращения ; При этом массу ротора удобнее
заменять двумя массами
тА
и mB,
сосредоточенными в цапфах
А и В (рис. 4.18), связанными между
собой невесомым стержнем. Тогда массы
цапф в объемах А и В определяются
по формулам
где G - сила тяжести ротора; GA и GB - составляющие силы тяжести в плоскостях еА и ев.
Рассматривая, например, цапфу А (рис.4.19), можно заметить, что динамическое давление подшипника на цапфу является лишь результатом смещения центра масс SA с оси вращения, то есть
QA=mA*w2 *рА.
О тсюда
смещение центра массы от оси вращения
будет составлять величину, равную
тсюда
смещение центра массы от оси вращения
будет составлять величину, равную
У читывая
соотношение (4.4), для цапфы
А принимается следующее
соотношение:
читывая
соотношение (4.4), для цапфы
А принимается следующее
соотношение:
Т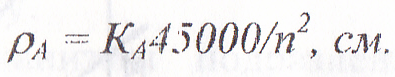 ак
как w=пП/30,
а
QсA
-KaGa,
выражение (4.5) преобразуется в следующее
равенство:
ак
как w=пП/30,
а
QсA
-KaGa,
выражение (4.5) преобразуется в следующее
равенство:
Величина рА, Шитиков предлагает эту величину брать в качестве критерия неуравновешенности. Очевидно, что для полной характеристики ротора необходимо учитывать и рв — величину смещения центра массы второй цапфы - цапфы В: рв =Кв45000/п2, см, где Кв= Qс B /Gв
Зная величины рА и рв, нетрудно определить значение допустимых дисбалансов Da и Db плоскостях еА и ев: Dа=тАрА; DB =тврв
О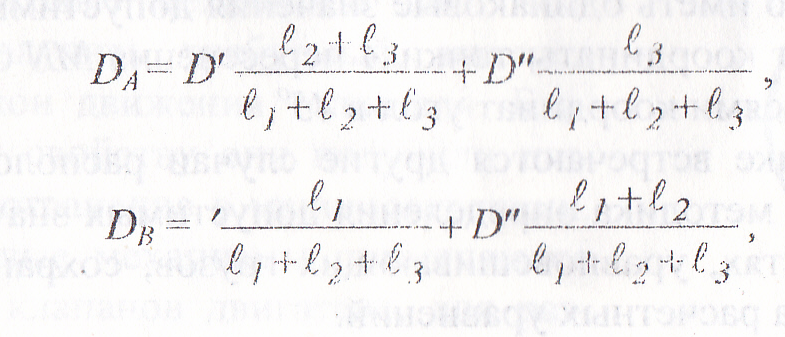 днако
при балансировке необходимо знать
допустимые значения дисбалансов не
в плоскостях подшипников еА и ев
в плоскостях е'и
е” где устанавливаются уравновешивающие
грузы. Уравнения для определения
D'
и
D"
допустимых значений дисбалансов в
плоскостях уравновешивания - примут
вид
днако
при балансировке необходимо знать
допустимые значения дисбалансов не
в плоскостях подшипников еА и ев
в плоскостях е'и
е” где устанавливаются уравновешивающие
грузы. Уравнения для определения
D'
и
D"
допустимых значений дисбалансов в
плоскостях уравновешивания - примут
вид
