Графическое изображение синусоидальных переменных величин

Практика остановила свой выбор на синусоидальных измене­ниях переменных электрических величин. В дальнейшем, говоря о переменном токе, э. д. с, напряжении и магнитном потоке, мы будем считать их изменяющимися по закону синуса.

Пусть мы имеем радиус-вектор ОA (рис. 124) произвольной длины. Будем вращать с постоянной скоростью вектор вокруг точки О против часовой стрелки. Конец вектора будет описывать окружность, а угол а, на который поворачивается вектор, будет меняться с течением времени.

Угловая скорость, или угловая частота и (омега), вращения равна углу поворота вектора в единицу вре­мени:

Следовательно, угол поворота вектора

 

Часто вместо градуса пользуются другой единицей измерения угла — радианом. Радианом называется угол, дуга которого равна радиусу. Так как длина окружности С = 2πR, то полному углу 360⁰   соответствует   радиан.

За один оборот радиус-вектор ОА будет иметь один период вра­щения продолжительностью Т сек.

Угловая частота в этом случае выразится так:

Так как    то 

 

Угол  поворота   радиуса-векто­ра  α   от   начального   положения будет равен 

 

 

 

 

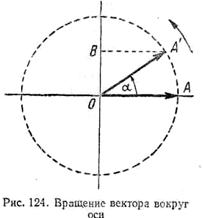
Угол   α   называется    фазным    у г л о м,    или    фазой. Проекция вектора ОА на вертикальный диаметр   равна  про­изведению величины вектора на синус фазного угла, т. е.

Следовательно, проекция вращающегося вектора ОА на вер­тикальный диаметр изменяется по закону синуса. Если длина век­тора будет А_m, то мгновенное значение проекции а равно

В последнем случае мгновенное значение проекции равно ее амплитудному или максимальному значению.

Задаваясь величиной. фазного угла и проектируя вектор А_m на вертикальный диаметр, будем получать мгновенное значение синусоидальной величины.

Таким образом, синусоидальная величина изображается вращаю­щимся вектором; длина вектора в масштабе выражает амплитуду синусоиды.

Проведем  горизонтальную ось,   на которой отложим фазные углы, проходимые вектором при его вращении (рис.  125). Откла­дываем затем вертикальные отрезки, равные соответствующим значениям проекции вращающегося вектора.

 

Соединяя концы вертикальных отрезков плавной кривой, получим знакомую нам кривую — синусоиду.

Способ изображения синусоидально изменяющихся величин с помощью векторов определенной длины и определенным образом расположенных друг относительно друга называется вектор­ной диаграммой,

Та же зависимость может быть выражена в виде синусоидальных кривых.

Таким образом, переменную синусоидальную величину можно представить тремя способами: уравнением, векторной диаграммой и графиком синусоиды.

 Если радиус-вектор в начальный момент отсчета времени (t = 0) составляет некоторый угол Ψ с горизонтальной осью, то в этом случае мгновенное значение переменной величины будет:

Угол Ψ (пси) называется начальным ф а з н ы м у г л о м,  или начальной   фазой.

Векторная диаграмма и график для этого случая даны на рис. 126.

Мы не внесем ничего нового, если будем вращать одновременно и с одинаковой скоростью со два вектора, совпадающие по направ­лению. В определенный момент времени оба вектора будут повер­нуты на один и тот же фазный угол. Поэтому как сами векторы,  так и переменные величины, которые они выражают, называют совпадающими по фазе. Векторная диаграмма и график двух величин, совпадающих по фазе, даны на рис. 127.

Уравнения для таких величин запишутся так:

 

 

 

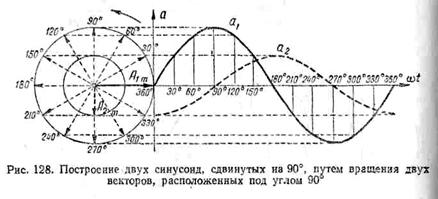
Если векторы сдвинуть один относительно другого на опре­деленный угол α и вращать их вокруг точки О, то мы получим две синусоидальные кривые, сдвинутые, как говорят, по фазе между собой на тот же угол α. На рис. 128 показано построение двух синусоид, сдвинутых но фазе на угол а, равный 90°. В этом случае о кривой а₁ говорят, что она опережает кривую а₂ по фазе на .90°, или, наоборот, кривая а₂ отстает по фазе от кривой а₁ на 90°.

27.