Что такое матрица Коши однородной системы линейных оду? Пример.
Рассмотрим систему линейных ДУ:
Система (1) называется ОДНОРОДНОЙ, если , в противном случае – НЕОДНОРОДНОЙ. Предположим, что и непрерывны на интервале . При этих условия на существует единственное решение системы (1), удовлетворяющее начальному условию:
Матричная запись.
В системе (1) обозначим через и столбцы:
А через обозначим -матрицу с элементами :
Тогда систему (1) можно записать в виде одного уравнения:
, и начальные условия:
Однородное уравнение:
Пусть имеется столбцов: Составим из них матрицу :
Сопоставим уравнению (2), правая и левая части которого – столбцы, аналогичное уравнение: , правая и левая части которого – матрицы размерности , и в котором неизвестной является матрица .
Теорема:
Пусть есть решений уравнения (2). Тогда -матрица , образованная из них, является решением матричного уравнения (3). И наоборот.
Определение:
Решение уравнения (3), для которого определитель Вронского (см. вопрос 16) отличен от нуля всюду на , называется ФУНДАМЕНТАЛЬНОЙ МАТРИЦЕЙ.
Теорема:
Линейная однородная система уравнений имеет фундаментальную матрицу.
Теорема:
Если - фундаментальная матрица, то любое решение уравнения (2) представимо в виде: , где - некоторый постоянный столбец.
Построим решение уравнения (2), удовлетворяющее начальным условиям, выразив с помощью величину через :
,
откуда и, следовательно, .
Матрицу , являющуюся функцией двух переменных, назовём ИМПУЛЬСНОЙ МАТРИЦЕЙ.
Теорема:
Решение задачи (2) с начальными условиями, имеет вид:
,
где матрица удовлетворяет по аргументу матричному уравнению (3) и условию
Пример: дана система:
найдём матрицу Коши этой системы.
Общее решение: =>
Сформулировать теорему Ляпунова об устойчивости и неустойчивости по первому приближению.
Решение задачи Коши для нормальной
системы ОДУ
непрерывно зависит от начальных условий
при
,
если правая часть
удовлетворяет условиям теорем
существования и единственности (СМ.
ВОПРОС 23!!!).
Но это было раньше. А теперь мы рассмотрим
зависимость задачи Коши от начальных
условий, когда
.
Будем предполагать, что для системы
уравнений (1) выполнены условия теорем
существования и единственности на
множестве таких точек
,
что
,
,
где
- открытое множество в пространстве
переменного
.
Пусть
- решение системы уравнений (1), определённое
при
.
Определение:
Решение
системы (1) называется УСТОЙЧИВЫМ ПО
ЛЯПУНОВУ, если для
,
решение
определено при
и
.
Если, кроме того,
,
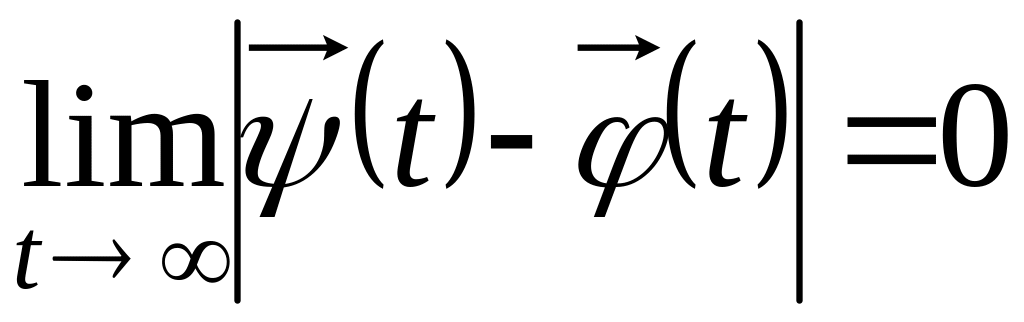то решение
называется асимптотически устойчивым.
Исследование на устойчивость по первому приближению.
Пусть
- положение равновесия для нормальной
системы ДУ:
,
правая часть которой удовлетворяет
условиям теорем существования и
единственности и имеет вид:
,
где
- квадратная матрица. Пусть также
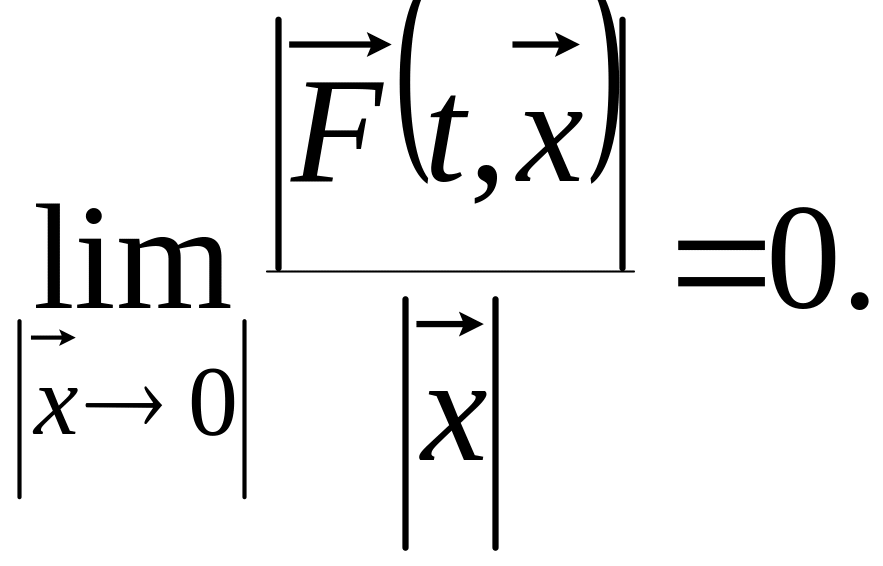Линейная однородная система ДУ
называется первым приближением или
линеаризацией исходной системы
уравнений (1) в окрестности точки
.
Заметим также, что
,
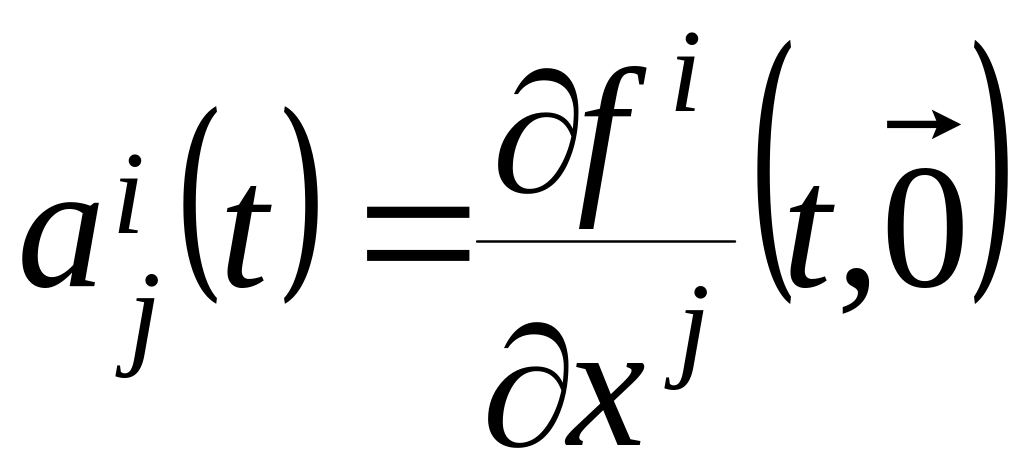- матрица Якоби.
Теорема Ляпунова:
Пусть имеется нормальная система уравнений:
,
,
где
- постоянная матрица, все собственные
значения которой имеют отрицательные
действительные части. Пусть также при
всех
и достаточно малом
:
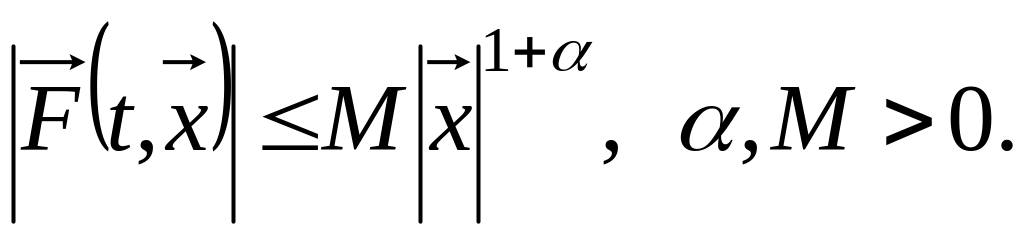
Тогда положение равновесия данной НС уравнений асимптотически устойчиво.
Теорема о неустойчивости:
Пусть задана нормальная система уравнений , с постоянной матрицей , имеющей хотя бы одно собственное значение с положительной действительной частью. Пусть при для достаточно малых значений выполнено неравенство:
Тогда положение равновесия данной системы уравнений неустойчиво.