Определение и свойства определителя Вронского, построенного из решений однородного оду -ого порядка. Пример.
Однородное линейное уравнение -ого порядка:
,
где коэффициенты
непрерывны на интервале
.
Определение:
Будем говорить, что функции ЛИНЕЙНО НЕЗАВИСИМЫ НА ИНТЕРВАЛЕ , если существуют постоянные , не все равные нулю, такие, что имеет место тождество:
В противном случае (т.е. если тождество выполняется только при ) будем говорить, что ЛИНЕЙНО НЕЗАВИСИМЫ.
Пусть - решения уравнения (1).
Определение:
Назовём детерминант
ОПРЕДЕЛИТЕЛЕМ ВРОНСКОГО.
Теорема:
Если решения
уравнения (1) линейно зависимы на
,
то
на
.
В самом деле, согласно тождеству (см.выше)
имеем
.
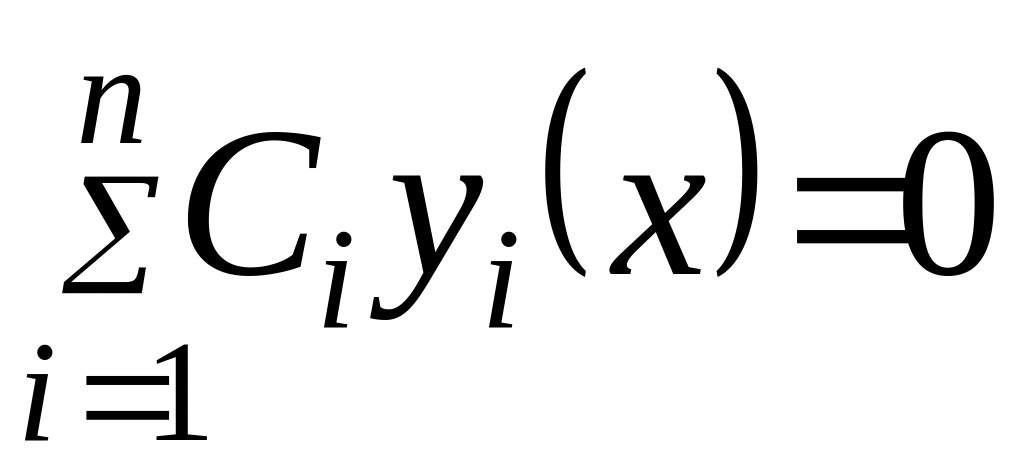Продифференцировав это тождество
раз, получим:
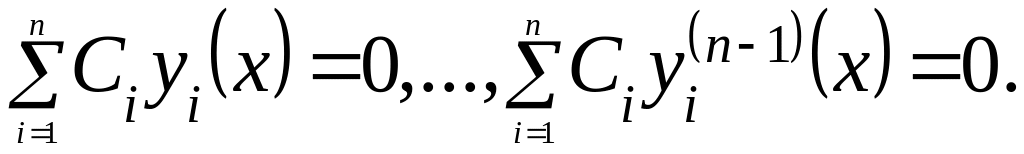
Теорема:
Если хотя бы для одного , то решения уравнения (1) линейно зависимы на .
Теорема:
Определитель Вронского либо тождественно равен нулю, и это означает, что решения линейно зависимы, либо не обращается в нуль ни в одной точке , и это означает, что линейно независимы.
Теорема:
Определитель Вронского ФСР (определённой
на отрезке
)отличен
от нуля во всех точках отрезка
.
Пример:
Найти определитель Вронского для функций
,
,
.
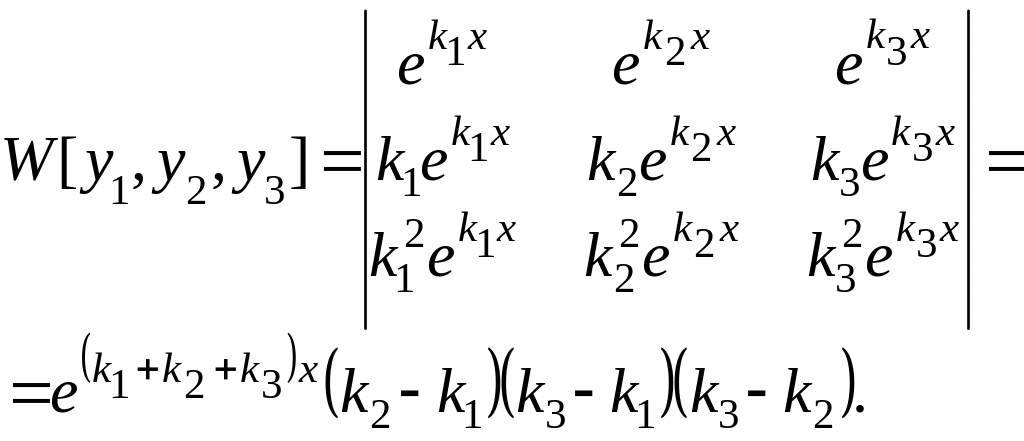
Сформулировать теорему существования и единственности решения задачи Коши для нормальной системы оду.
Определение:
НОРМАЛЬНОЙ СИСТЕМОЙ (НС) линейных дифференциальных уравнений называется система вида:
где
- квадратная матрица
,
а
- заданная вектор-функция, определённые
при
Определение:
ОДНОРОДНОЙ СИСТЕМОЙ (ОС) линейных ДУ, соответствующей системе (1), называется система уравнений:
Теорема:
Пусть матрица системы (1)
и
.
Тогда решение задачи Коши для системы
(1) с начальным условием
единственно на отрезке
Алгоритм решения задачи Коши для линейного неоднородного оду -ого порядка с нулевыми начальными условиями с помощью функции Коши. Пример.
.
Теорема:
Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения
Задача Коши для линейного неоднородного уравнения:
состоит в следующем: найти решение этого уравнения, удовлетворяющее начальным условиям (данным Коши):
.
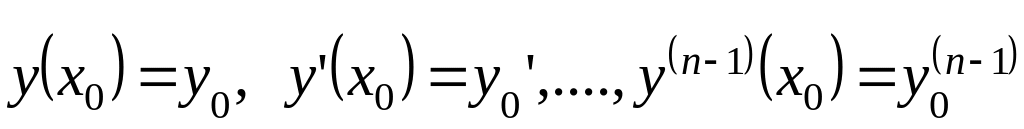Определение:
ФСР однородного уравнения будем называть любые линейно независимых решений этого уравнения.
Теорема (другая формулировка первой теоремы):
Если - фундаментальная система решений однородного уравнения (с такой же левой частью, как и уравнения (1)), а - частное решение неоднородного уравнения (1), то любое решение неоднородного уравнения (1) представимо в виде:
,
где
- некоторые постоянные.
Доказательство:
Рассмотрим разность
.
Согласно теореме* (*: разность двух
решений неоднородного линейного
уравнения удовлетворяет однородному
уравнению) эта разность удовлетворяет
однородному уравнению, и, значит:
.
Т.о., для построения общего решения неоднородного уравнения нужно помимо ФСР однородного уравнения знать хотя бы одно частное решение неоднородного уравнения.
Алгоритм:
Покажем, что, зная ФСР, можно найти квадратурой некоторое частное решение неоднородного уравнения. Зададимся целью построить частное решение , удовлетворяющее нулевым начальным условиям:
Представим
приближённо как сумму функций (элементарных
воздействий), равных
в промежутке
и нулю в остальных точках. Решение
,
отвечающее каждой такой элементарной
функции, имеющее пир
равные нулю производные до
-ого
порядка включительно, является
тождественным нулём вплоть до
,
но:
Т.е.
равно уже не нулю, а
и, таким образом, далее решение также
будет не нулём. В силу принципа суперпозиции
достаточно построить решение однородного
уравнения (ведь вне
правая часть равна нулю), принимающее
в точке
нулевое значение вместе с производными
до
-ого
порядка включительно и с производной
-ого
порядка, равной единице (обозначим это
решение
,
указывая зависимость от начальной
точки, и назовём его ИМПУЛЬСНОЙ
ФУНКЦИЕЙ), а затем умножить его на
.
Итак,
строится как решение однородного
уравнения, удовлетворяющее условиям:
.
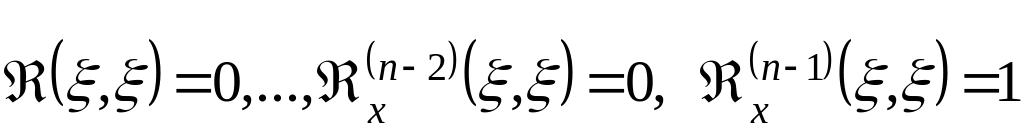А решение, отвечающее элементарному
воздействию, имеет вид
.
Суммируя теперь элементарные воздействия
на основании того же принципа суперпозиции
и переходя от суммы к интегралу, получим
решение
,
удовлетворяющее нулевым начальным
условиям:
.
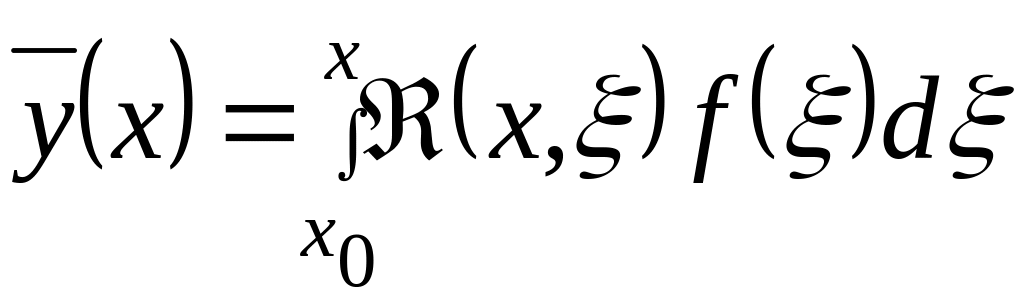Пример:
Общее решение: