Сформулировать теорему о структуре фср однородного линейного уравнения -ого порядка с постоянными коэффициентами в случае простых корней характеристического уравнения. Пример.
Однородное линейное уравнение -ого порядка:
,
коэффициенты которого
непрерывны на интервале
.
Определение:
Будем говорить, что функции
ЛИНЕЙНО ЗАВИСИМЫ НА ИНТЕРВАЛЕ
,
ЕСЛИ СУЩЕСТВУЮТ ПОСТОЯННЫЕ
,
не все равные нулю, такие что имеет место
тождество:
В противном случае (т.е. если (2) выполняется
только при
)
будем говорить, что
ЛИНЕЙНО НЕЗАВИСИМЫ.
Пусть
- решения уравнения (1).
Определение:
Назовём детерминант:
ОПРЕДЕЛИТЕЛЕМ ВРОНСКОГО.
Теорема:
Если решения уравнения (1) линейно зависимы на , то на .
Теорема:
Если
хотя бы для одного
,
то решения
уравнения (1) линейно зависимы на
.
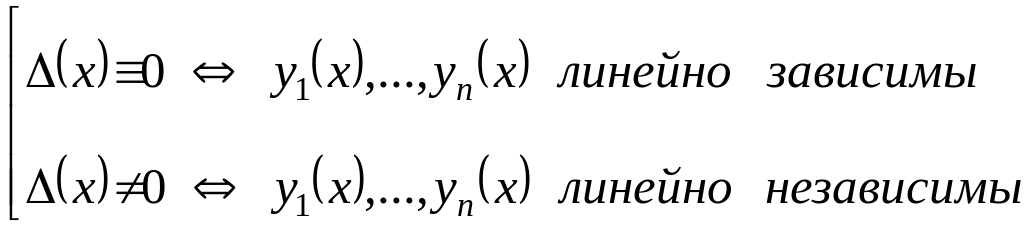при
.
Определение:
ФУНДАМЕНТАЛЬНОЙ СИСТЕМОЙ РЕШЕНИЙ уравнения (1) будем называть любые линейно независимых решений.
Теорема:
Линейное однородное уравнение имеет ФСР.
Теорема:
Если - фундаментальная система решений, то любое решение уравнения (1) представимо в виде:
Где
- некоторые постоянные.
Ищем решение в виде:
- характеристическое уравнение.
Если все
- ВЕЩЕСТВЕННЫЕ И РАЗЛИЧНЫЕ, то общее
решение:
,
Пример:
Теорема:
Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения и какого-либо частного решения неоднородного уравнения.
Сформулировать определение матрицы Коши однородной системы оду. Пример.
Определение:
Матрица
называется МАТРИЦЕЙ КОШИ, «ИМПУЛЬСНОЙ
МАТРИЦЕЙ» или МАТРИЦИАНТОМ. Она
однозначно определяется как решение
задачи Коши:
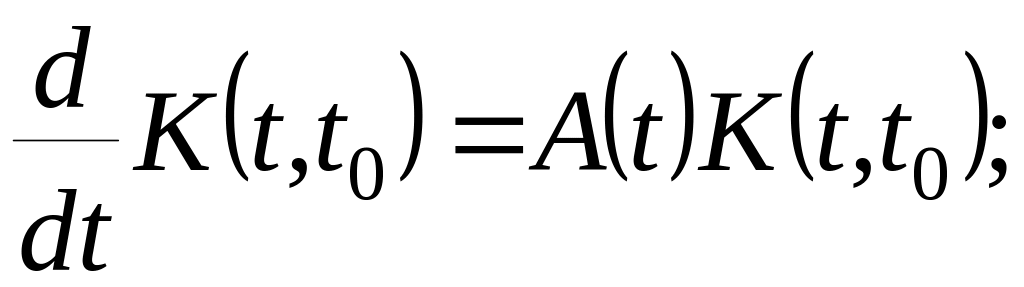
Замечание:
Для построения матрицы Коши надо решить векторных задач Коши:
Решение задачи Коши для нормальной
системы
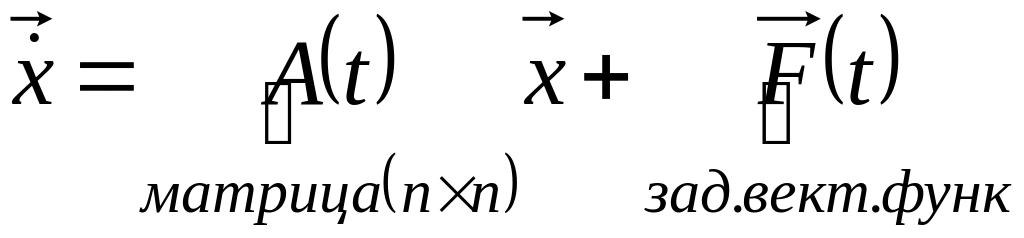
Имеет вид:
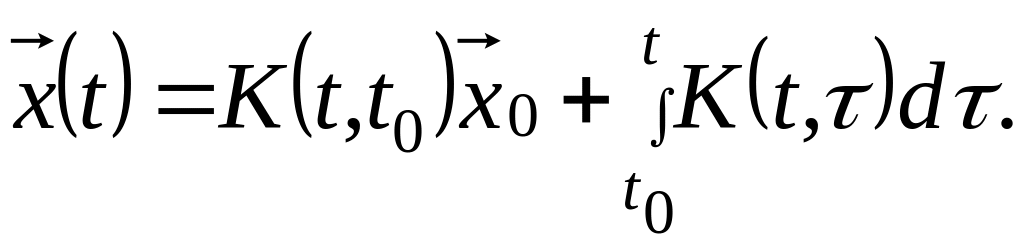
Теорема:
ФСР однозначно определяет нормальную
форму линейной ОС, т.е. матрицу
.
Иначе говоря, зная фундаментальную
матрицу
системы, можно однозначно восстановить
эту систему уравнений.
Пример:
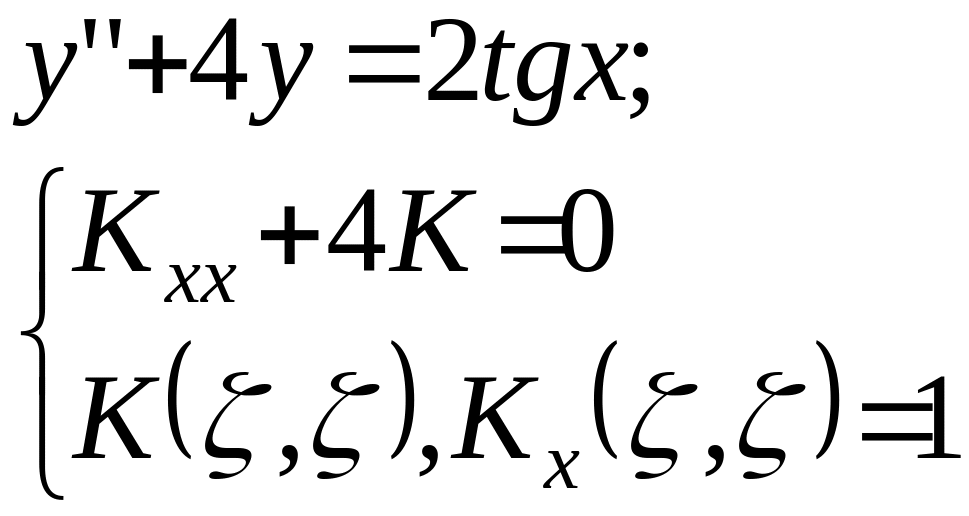
Общее решение:
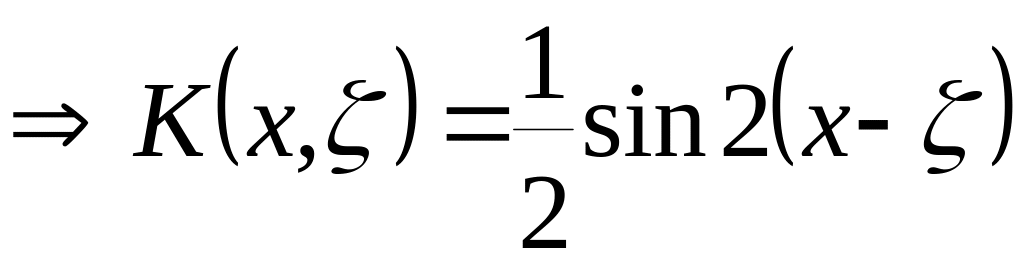
Алгоритм решения линейного неоднородного оду -ого порядка с помощью функции Коши. Пример.
НЕОДНОРОДНОЕ УРАВНЕНИЕ:
.
Теорема:
Если
- фундаментальная матрица, а
- частное решение неоднородного уравнения
(1), то любое решение
уравнения (1) представимо в виде:
,
Где
- некоторые постоянный столбец.
Теорема:
Частное решение
уравнения (1), удовлетворяющее решению
,
имеет вид:
,
где
- ИМУЛЬСНАЯ МАТРИЦА – решение матричного
уравнения
.,
удовлетворяющее условию
Пример:
Общее решение:
Определение и свойства фундаментальной матрицы однородной линейной системы оду. Пример.
ОДНОРОДНОЕ УРАВНЕНИЕ:
Пусть имеется столбцов:
Составим из этих столбцов матрицу :
Сопоставим уравнению (1), правая и левая части которого – столбцы, аналогичное уравнение: , правая и левая части которого – матрицы размерности и в котором неизвестной является матрица .
Теорема:
Пусть есть решений уравнения (1). Тогда -матрица , образованная из них, является решением матричного уравнения. И наоборот.
Определение:
ФУНДАМЕНТАЛЬНОЙ СИСТЕМОЙ РЕШЕНИЙ уравнения (1) будем называть линейно независимых решений уравнения (1), а соответствующую им матрицу будем называть ФУНДАМЕНТАЛЬНОЙ МАТРИЦЕЙ.
Определение:
Решение
уравнения (2) , для которого
отлично от нуля всюду на
,
называется ФУНДАМЕНТАЛЬНОЙ МАТРИЦЕЙ.
Теорема:
Линейная однородная система уравнений имеет фундаментальную матрицу.
Теорема:
Если - фундаментальная матрица, то любое решение уравнения (1) представимо в виде:
,
Где - некоторый постоянный столбец.
Пример: Решить систему:
Составляем и решаем характеристическое уравнение:
Для корня находим собственный вектор :
Можно взять Имеем частное решение:
, Чтобы получить два вещественных решения, надо взять вещественную и мнимую части найденного комплексного решения. Так как
, то:
Общее решение выражается через два найденных линейно независимых решения: