7. Метод вариации постоянной для решения неоднородной линейной нормальной системы оду первого порядка. Пример.

Нам дана система трёх неоднородных уравнений:

Будем предполагать, что общее решение соответствующей однородной системы уже найдено:

Решение неоднородной системы ищем в виде:

Где - пока неизвестные функции.

Подставим третью систему в первую, тогда:

Все суммы, стоящие в скобках, обратятся в ноль. Таким образом:

Аналогично получим:

Система уравнений, линейных относительно , имеет решение, т.к. её определитель: в силу линейной независимости частных решений соответствующей однородной системы. Отыскав , затем с помощью интегрирования найдём , а тем самым и решение неоднородной системы.

Пример:

Определение:

НОРМАЛЬНОЙ СИСТЕМОЙ (НС) линейных дифференциальных уравнений называется система вида:

,

Где - квадратная матрица , а - заданная вектор-функция.

7. Покажите равносильность задачи Коши для ОДУ -ого порядка задаче Коши для нормальной системы 1ого порядка. Пример.

Рассмотрим линейное дифференциальное уравнение (ЛДУ) -ого порядка:

.

Введём вектор-функцию:

Которая удовлетворяет системе линейных ДУ: , где - квадратная матрица ,

Итак, ЛДУ -ого порядка сводится к линейной системе первого порядка из ДУ. При этом, если - какое-либо решение ЛДУ, то - решение системы. Аналогично и обратное, причем , .

Задача Коши для ЛДУ: найти решение первого уравнения, удовлетворяющее начальным условиям:

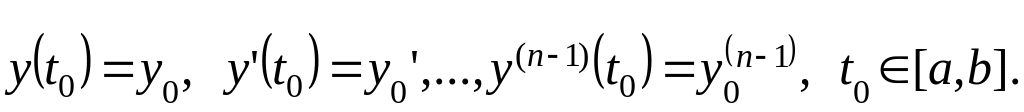
Сводя первое уравнение к системе уравнений, мы одновременно сводим и задачу Коши, т.к. начальные условия (см. выше) записываются в виде начальных условий для системы:

Пример:

Задача Коши для уравнения второго порядка.

Обозначим , тогда эквивалентная задача Коши для нормальной системы имеет вид:

7. Сформулировать теорему о существовании и единственности решения задачи Коши для системы уравнений первого порядка.

Задача для нормальной систему ОДУ состоит в отыскании решения , удовлетворяющего начальным условиям

Предположим, что выполнены следующие условия:

Условие 1: Пусть , т.е. существует постоянная , следовательно, - равномерно ограничена в

Условие 2: Пусть в любой замкнутой ограниченной подобласти удовлетворяет УСЛОВИЮ ЛИПШИЦА по переменной , т.е. существует постоянная Липшица такая, что для всех и выполняется неравенство:

Теорема:

Пусть выполнены условия 1 и 2, тогда на отрезке существует, и при том единственное, решение задачи Коши.

7. Что такое фундаментальная матрица? Как с её помощью построить общее решение однородной системы? Пример.

ОДНОРОДНОЕ УРАВНЕНИЕ:

Пусть имеется столбцов:

Составим из этих столбцов матрицу :

Сопоставим уравнению (1), правая и левая части которого – столбцы, аналогичное уравнение: , правая и левая части которого – матрицы размерности и в котором неизвестной является матрица .

Теорема:

Пусть есть решений уравнения (1). Тогда -матрица , образованная из них, является решением матричного уравнения. И наоборот.

Определение:

ФУНДАМЕНТАЛЬНОЙ СИСТЕМОЙ РЕШЕНИЙ уравнения (1) будем называть линейно независимых решений уравнения (1), а соответствующую им матрицу будем называть ФУНДАМЕНТАЛЬНОЙ МАТРИЦЕЙ.

Пример: Решить систему:

Составляем и решаем характеристическое уравнение:

Для корня находим собственный вектор :

Можно взять Имеем частное решение:

, Чтобы получить два вещественных решения, надо взять вещественную и мнимую части найденного комплексного решения. Так как

, то:

Общее решение выражается через два найденных линейно независимых решения:

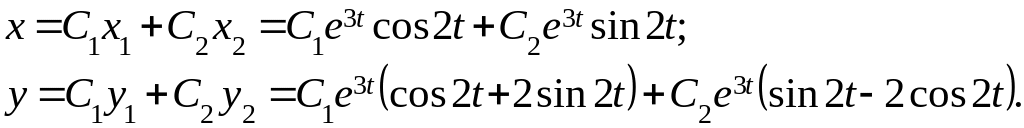
7. Сформулировать теорему существования и единственности решения задачи Коши для уравнения -ого порядка, разрешённого относительно старшей производной.

Общие свойства линейного уравнения -ого порядка:

Определение:

Уравнение (1) называется ОДНОРОДНЫМ, если , в противном случае – НЕОДНОРОДНЫМ.

Пусть непрерывны на некотором интервале ( может быть как конечным интервалом, так и бесконечным). Общая теорема существования и единственности гарантирует, что на некотором сегменте , принадлежащем , существует единственной решение уравнения (1), удовлетворяющее начальному условию:

Теорема:

Если , непрерывны на , то решение начальной задачи (1) и (2) существует и единственно всюду на .

Т.к. начальная задача для уравнения -ого порядка является частным случаем начальной задачи для системы уравнений первого порядка, то предыдущую теорему можно получить как частный случай аналогичного утверждения для системы линейных уравнений, которая имеет вид:

а соответствующие начальные условия:

Теорема:

Если 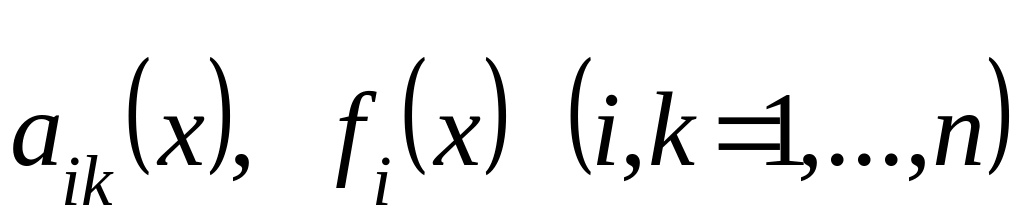непрерывны на , то решение задачи (3), (4) существует и единственно на .