Алгоритм построения функции Грина и решения первой краевой задачи для неоднородного дифференциального уравнения 2-ого порядка.
Определение и алгоритм построении функции Грина первой краевой задачи.
Определении ф-ии Грина – см. 39.
Покажем теперь, что функция Грина существует и дадим алгоритм её построения.
Построим функцию
,
являющуюся решением однородного
уравнения (1) и удовлетворяющую левому
краевому условию:
.
Функция
может быть построена как решение
начальной задачи для уравнения (1) с
начальными условиями:
,
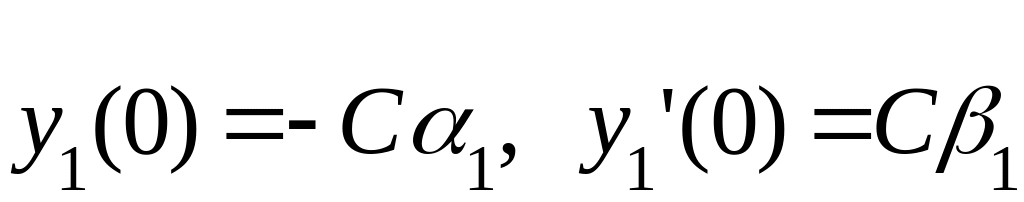где
- произвольная постоянная. Аналогично
построим функцию
,
являющуюся решением однородного
уравнения и удовлетворяющую правому
граничному условию:
Эти две построенные функции линейно
независимы.
Будем искать функцию в виде:
Постоянные и находим из соотношений:
Определитель этой линейной алгебраической системы представляет собой определитель Вронского линейно независимых решений и и отличен от нуля:
,
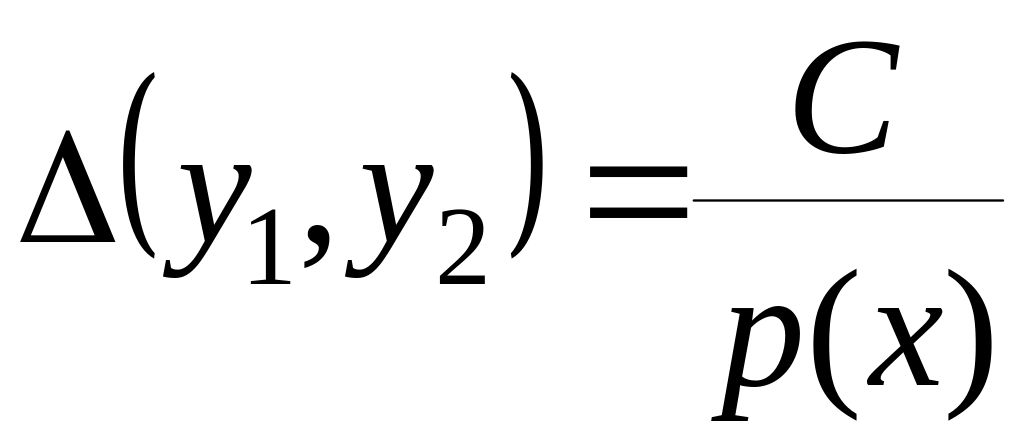С определяется нормировкой решений
и
.
Используя полученные значения и , получим окончательное выражение функции Грина краевой задачи (1):
Где постоянная
Алгоритм:
Пусть найдено общее решение
линейного однородного уравнения с той
же левой частью. Тогда решение уравнения
(1) ищется в виде:
Функции
определяются из системы:
