7. Сформулируйте теорему Нагумо о существовании решения нелинейной краевой задачи.

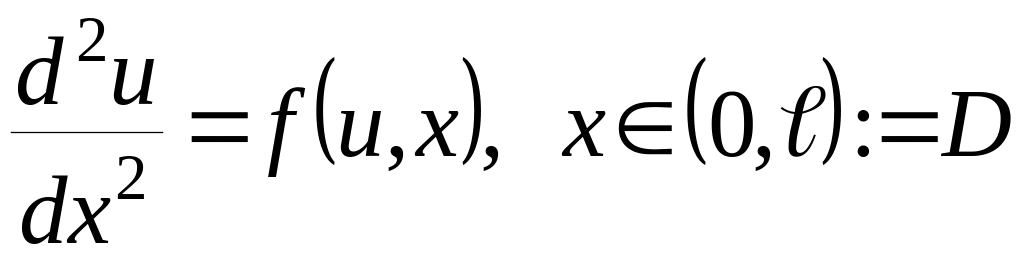
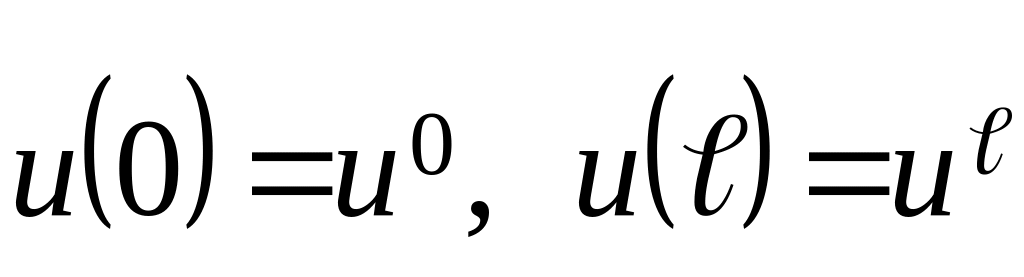
Определение:

Функции и называются соответственно НИЖНИМ и ВЕРХНИМ решениями краевой задачи (1), если выполняются неравенства:

, ;

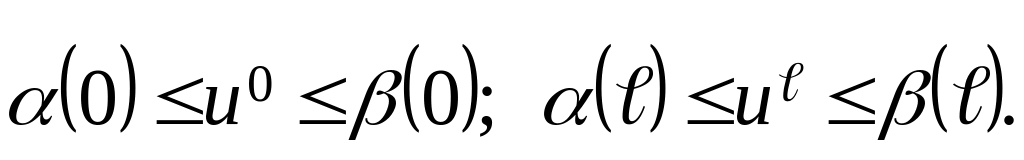
Теорема (Нагумо):

Пусть существуют и - нижнее и верхнее решения задачи (1), причем . Пусть - непрерывная и удовлетворяющая условию Липшица , . Тогда существует решение задачи (1) , удовлетворяющее неравенствам:

7. Сформулируйте теорему о представлении решения краевой задачи с помощью функции Грина.

Рассмотрим краевую задачу:

Здесь - непрерывные функции переменной ; - искомое решение; - заданные параметры, некоторые из которых могут быть равны 0, но и . Если , то граничные условия называются условиями 1ого рода. Если ,то – условиями 2ого рода. Если и , то – граничными условиями 3его рода. Если , то граничные условия называются однородными, в ином случае – неоднородными.

Будем искать в виде , где - любая дважды дифференцируемая функция, удовлетворяющая граничным условиям задачи (1). Для функции получаем задачу с однородными граничными условиями:

Где .

Рассмотрим вопрос единственности решения задачи (1). Пусть существуют два решения и . Тогда для функции из (1) получаем:

Если задача (2) имеет лишь тривиальное решение, то решение (1) единственно. Рассмотрим этот случай.

Теорема:

Пусть функции и непрерывны при 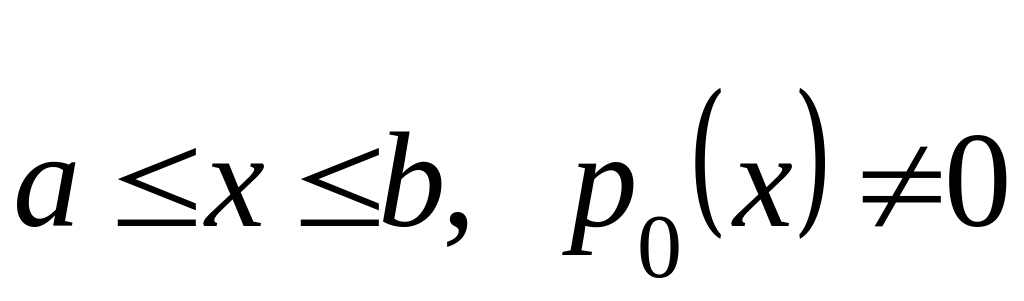. Тогда существует функция , называемая ФУНКЦИЕЙ ГРИНА, удовлетворяющая следующим требованиям:

1). как функция , при любом удовлетворяет однородному уравнению (*) при .

2). как функция переменной , удовлетворяет граничным условиям задачи (*).

3). непрерывна при .

4). Первая производная имеет при разрыв с величиной скачка предельных значений

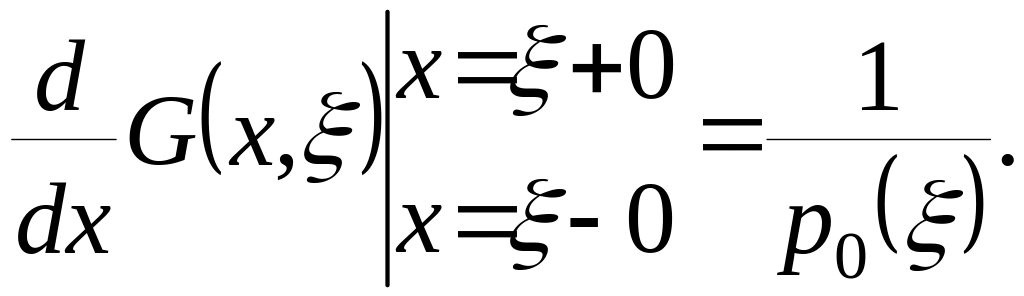
Решение краевой задачи (*) представимо в виде:

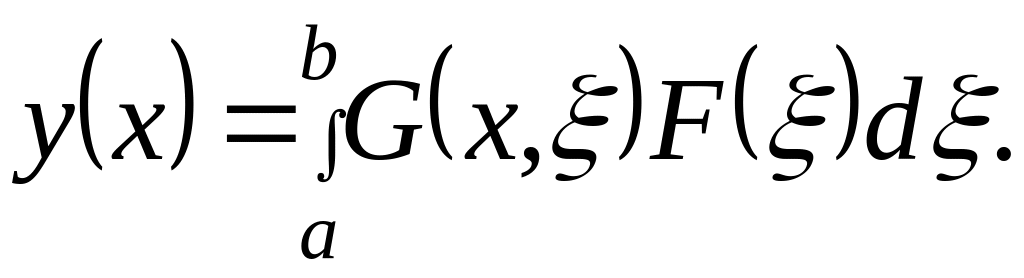
Функция Грина в явном виде определяется выражением:

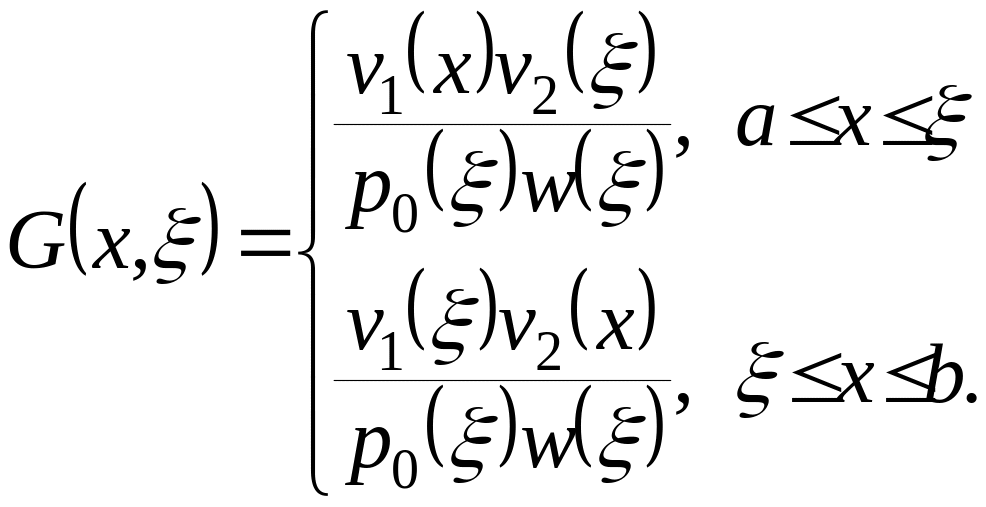
Где - произвольное нетривиальное решение однородного уравнения задачи (*), удовлетворяющее условию ; ; - определитель Вронского этих двух решений.

7. Сформулировать определение функции Грина краевой задачи для дифференциального уравнение второго порядка.

Рассмотрим краевую задачу:

.

Пусть функция положительна и непрерывно дифференцируема на , а действительные функции и непрерывны на . Решением краевой задачи (1) будем называть непрерывно дифференцируемую функцию с непрерывной второй производной на , удовлетворяющую на уравнению и граничным условиям (1). Если решение данной задачи существует, то оно единственно.

Предположим, что решение задачи (1) при функции , отличной от нуля, существует лишь в -окрестности некоторой фиксированной точки :

Причем функция и

Решение этой задачи будем обозначать функцией . Интегрируя уравнение (1) с так заданной функцией по отрезку , получим:

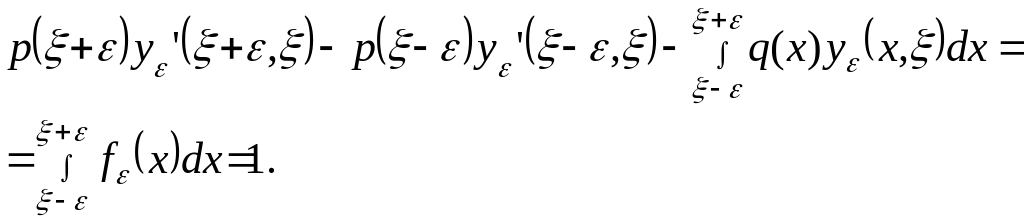
При : 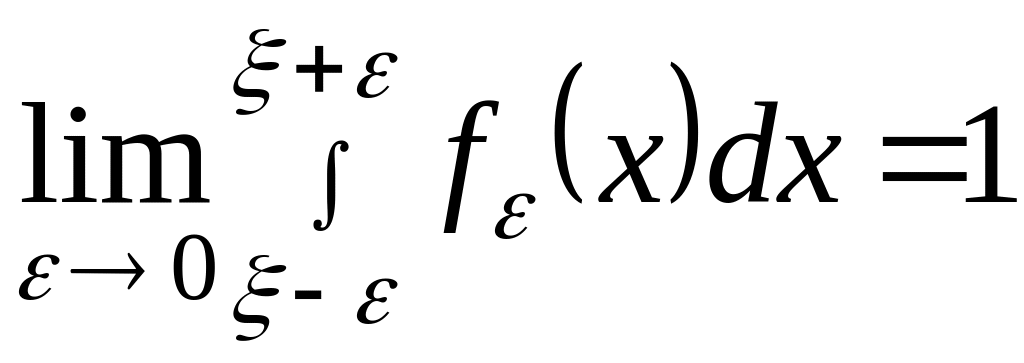. Будем предполагать, что предельная функция 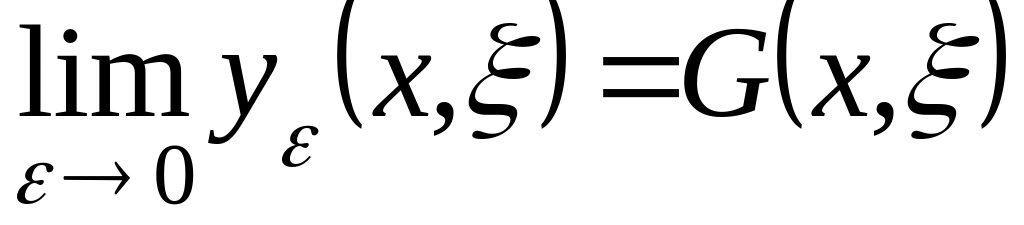существует и непрерывна на Тогда получается, что производная этой функции в точке должна иметь разрыв первого рода, причем разность правого и левого предельного значений этой производной определяется как:

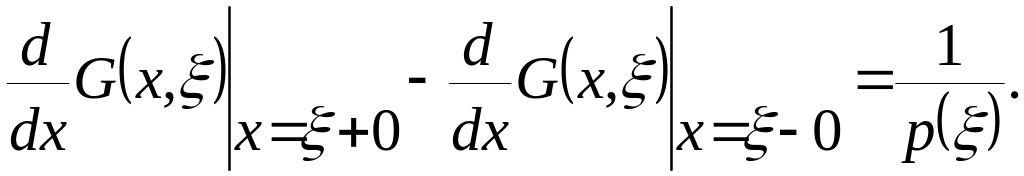
Если функция существует таки, то она подчиняется следующим условиям:

1). Как функция переменной она удовлетворяет однородному уравнению (1) при и ;

2). Она удовлетворяет граничным условиям (1);

3). Эта функция непрерывна на , а её первая производная имеет в точке разрыв первого рода с величиной скачка

Функцию, удовлетворяющую условиям 1), 2), 3), назовём ФУНКЦИЕЙ ГРИНА краевой задачи (1). Существенное значение функции Грина заключается в том, что через неё может быть выражено решение краевой задачи (1) с произвольной правой частью .