7. Сформулируйте критерий устойчивости решений линейных дифференциальных уравнений с постоянными коэффициентами. Пример.

Решение задачи Коши для нормальной системы ОДУ непрерывно зависит от начальных условий при , если правая часть удовлетворяет условиям теорем существования и единственности (СМ. ВОПРОС 23!!!).

Но это было раньше. А теперь мы рассмотрим зависимость задачи Коши от начальных условий, когда . Будем предполагать, что для системы уравнений (1) выполнены условия теорем существования и единственности на множестве таких точек , что , , где - открытое множество в пространстве переменного . Пусть - решение системы уравнений (1), определённое при .

Определение:

Решение системы (1) называется УСТОЙЧИВЫМ ПО ЛЯПУНОВУ, если для , решение определено при и .

Если, кроме того, , то решение называется асимптотически устойчивым.

Исследование на устойчивость по первому приближению.

Пусть - положение равновесия для нормальной системы ДУ:

,

правая часть которой удовлетворяет условиям теорем существования и единственности и имеет вид: , где - квадратная матрица. Пусть также Линейная однородная система ДУ называется первым приближением или линеаризацией исходной системы уравнений (1) в окрестности точки .

Теорема:

Для того, чтобы положение равновесия системы уравнений (1) было асимптотически устойчивым, необходимо и достаточно, чтобы все собственные значения матрицы имели отрицательные действительные части (примеры см. в 27 и 29).

7. Сформулировать теорему о достаточных условиях устойчивости системы линейных ду с постоянными коэффициентами.

Всё остальное бери из 30!

Рассмотрим однородную систему из ЛДУ: , где - постоянная действительная матрица. Пусть , , - собственные значения матрицы .

Лемма:

Пусть , тогда для любого решения системы (1) , удовлетворяющего начальному условию , выполнена равномерная на промежутке оценка:

.

Теорема:

Для того, чтобы положение равновесия системы уравнений (1) было асимптотически устойчивым, необходимо и достаточно, чтобы все собственные значения матрицы имели отрицательные действительные части (примеры см. в 27 и 29).

Доказательство:

1). Достаточность. Пусть - произвольное положительное число, а решение системы уравнений (1), удовлетворяющее начальному условию . В силу Леммы справедлива равномерная оценка:

, где - некоторые постоянные.

Пусть , тогда если , то , при всех , т.е. положение равновесия устойчиво по Ляпунову. Т.к. , то 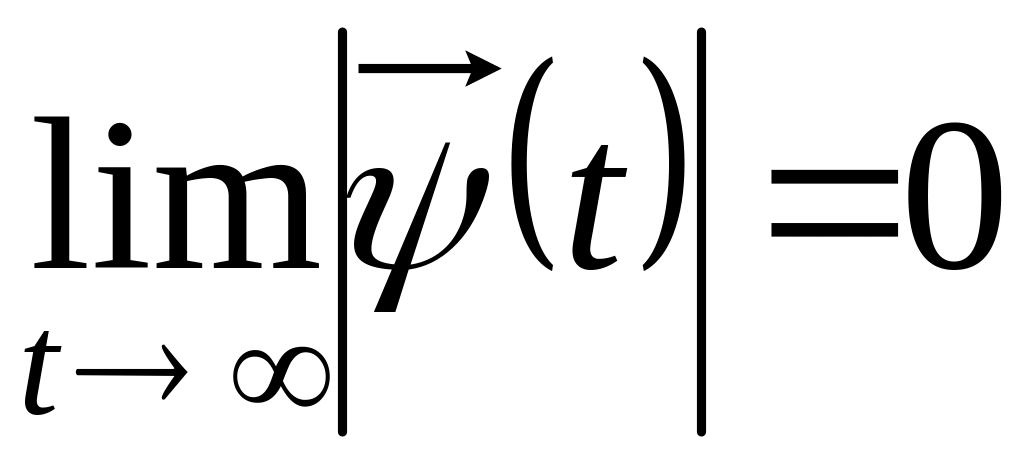, следовательно, положение равновесия асимптотически устойчива. Достаточность доказана.

7. Какое положение равновесия линейной динамической системы на плоскости называется устойчивым узлом? Неустойчивым узлом? Пример.

8. Какое положение равновесия ЛДС на плоскости называется устойчивым фокусом? Неустойчивым фокусом? Пример.

9. Какое положение равновесия ЛДС на плоскости называется седлом? Что можно сказать про устойчивость седла? Пример.

10. Какое положение равновесия ЛДС на плоскости называется центром? Что можно сказать про устойчивость центра? Пример.

Методы решения

Переходим в новую систему координат: ; - решение уравнения, которое мы исследуем.

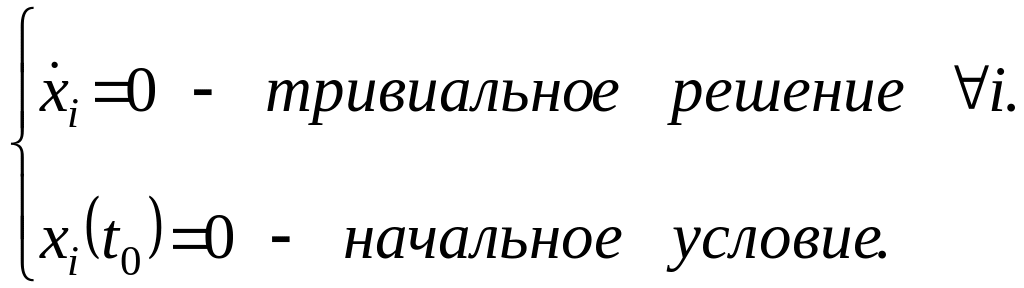
Тривиальное решение – маленькое отклонение от нуля начального условия.

Рассмотрим пример:

и Точка , в которой правые части уравнений системы обращаются в ноль – ТОЧКА ПОКОЯ СИСТЕМЫ.

Характеристическое уравнение:

и

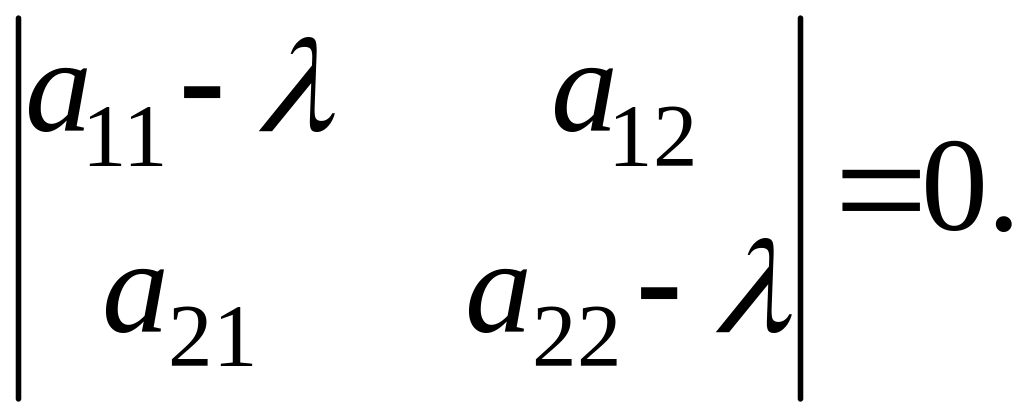
Итак, в зависимости от того, какими окажутся наши , различают несколько видов положения равновесия.

1). и - действительны и различны.

Тогда:

а). и : т.п. асимптотически устойчива.

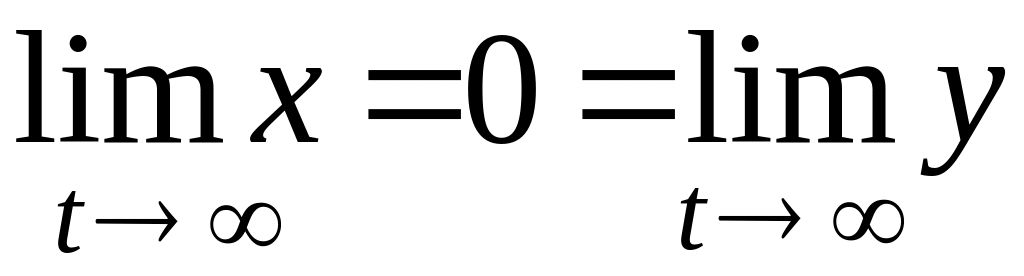- УСТОЙЧИВЫЙ УЗЕЛ

б ). -

т.п. неустойчива

НЕУСТОЙЧИВЫЙ УЗЕЛ

в). 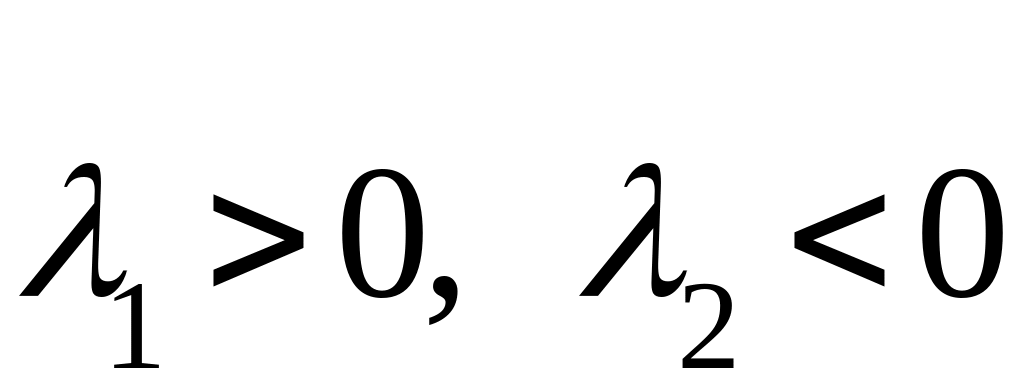(или наоборот)

точка покоя неустойчивая.

СЕДЛО

2).

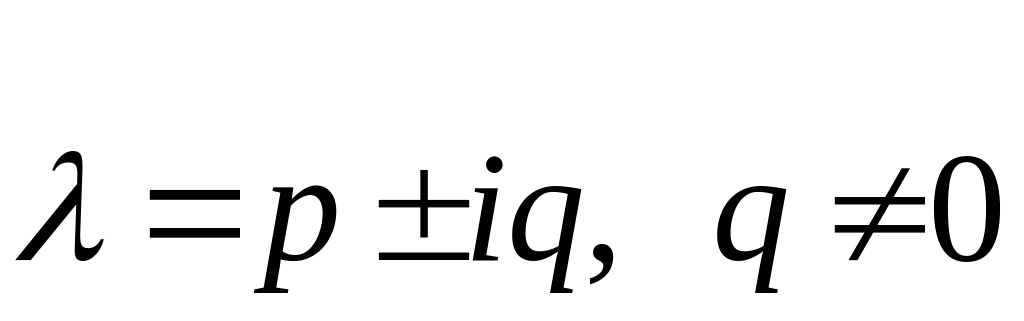
и - некие линейные комбинации и .

а).

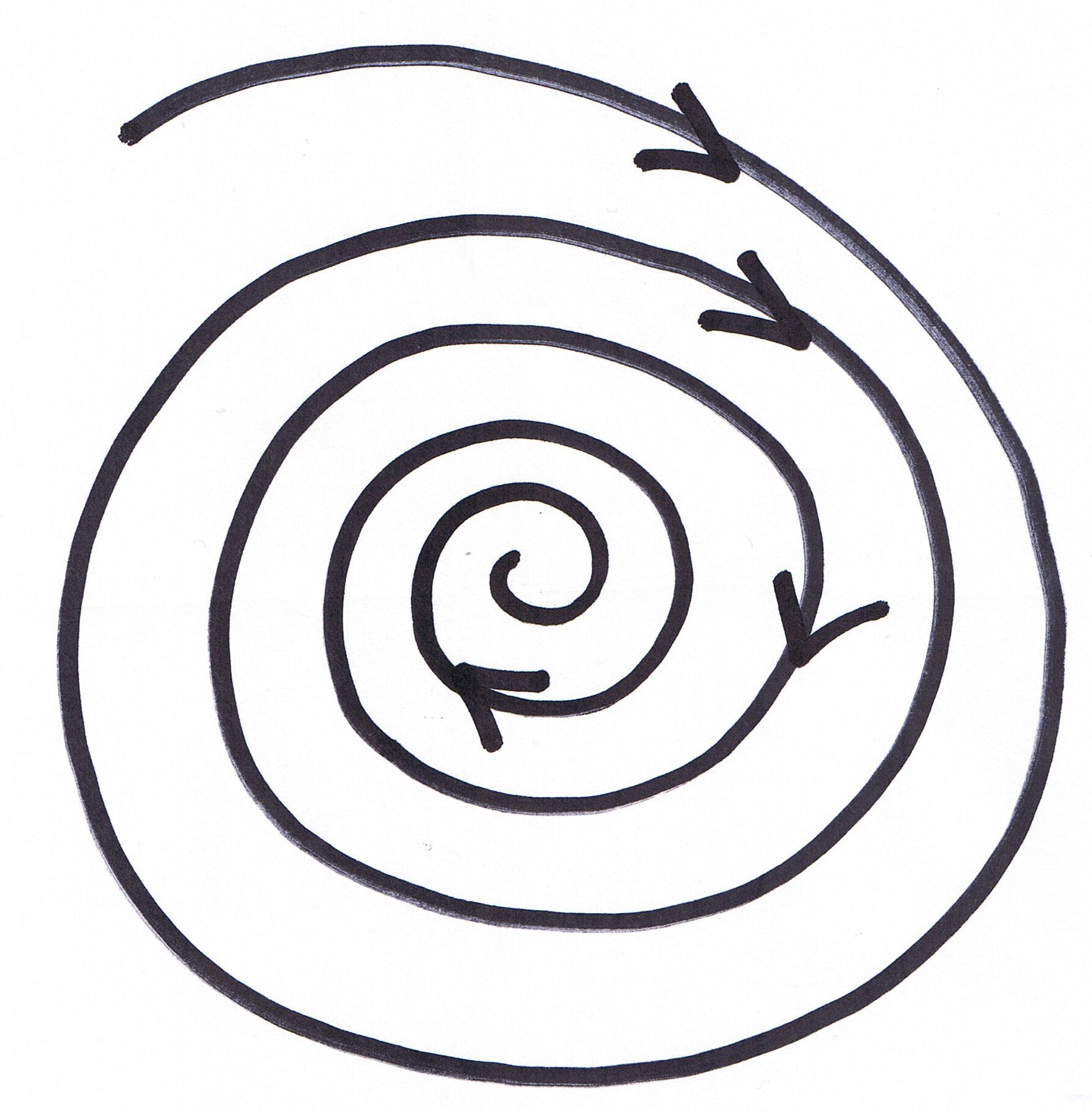
УСТОЙЧИВЫЙ ФОКУС

Фокус отличается от узла тем, что касательные к

траекториям не стремятся к определённому

пределу при приближении точки касания к

точке покоя.

Т.п. асимптотически устойчива.

б).

НЕУСТОЙЧИВЫЙ ФОКУС

т .п. неустойчива

в).

ЦЕНТР

Траектории – замкнутые кривые,

содержащие внутри себя точку покоя,

которая называется ЦЕНТР.

ЦЕНТР устойчив, но

асимптотической устойчивости нет.

Т.п. устойчива.

3). и - оба кратные.

а ).

Т.п. асимптотически устойчива

УСТОЙЧИВЫЙ

УЗЕЛ

Если -

- дикритический узел.

б).

НЕУСТОЙЧИВЫЙ УЗЕЛ

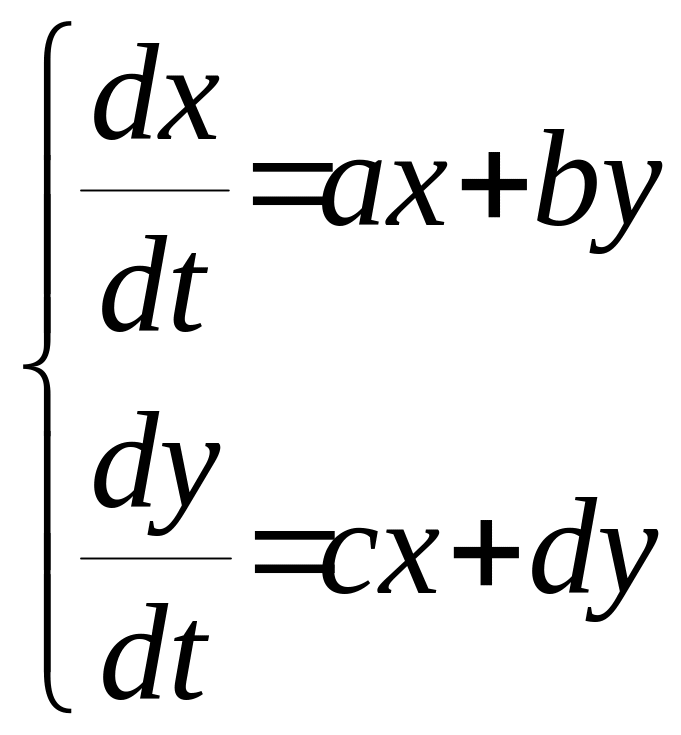
Т.п. неустойчива.

Пример 1.

Провести классификацию особых точек уравнения:

; ;

особая точка «СЕДЛО».

Подставляем в уравнение ; .

,

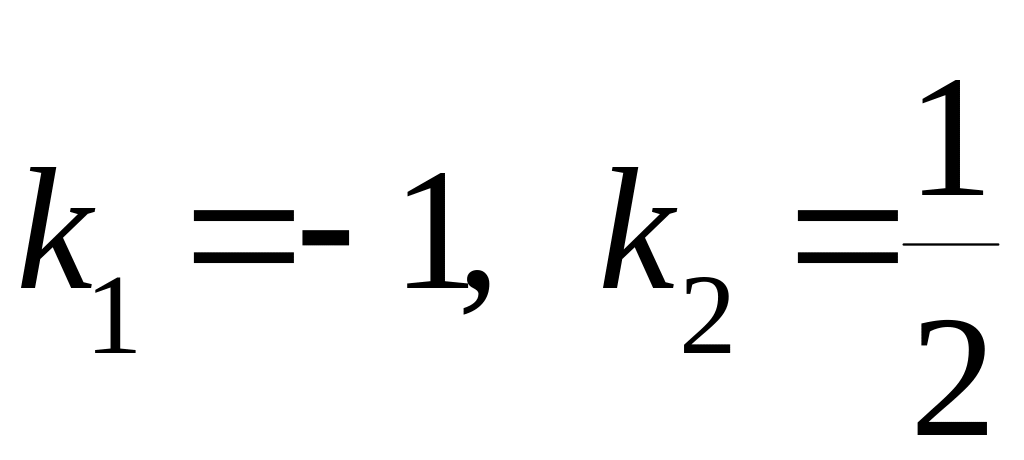Пример 2.

; ;

особая точка «УСТОЙЧИВЫЙ УЗЕЛ».

Пример 3.

Исследовать на устойчивость по первому приближению.

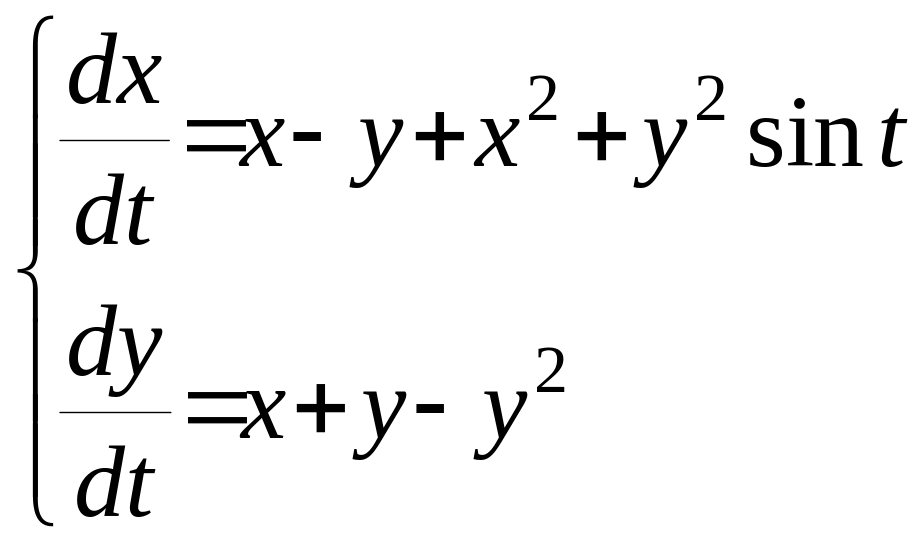Все степени больше первой – выкидываем нахрен.

Итак.

; .

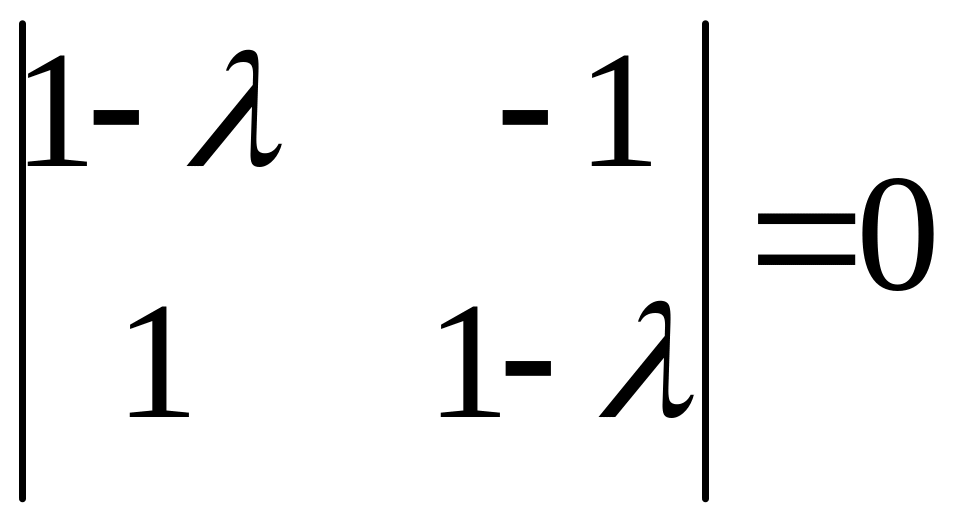точка покоя неустойчивая.

7. Сформулировать теорему о единственности решения краевой задачи и теорему и достаточных условиях существования только тривиального решения у однородной краевой задачи с краевыми условиями первого рода.

Краевыми задачами для ОДУ называются задачи, в которых дополнительные условия ставятся в нескольких точках.

Рассмотрим линейное ОДУ 2-ого порядка:

с дополнительными условиями первого рода (задача Дирихле):

,

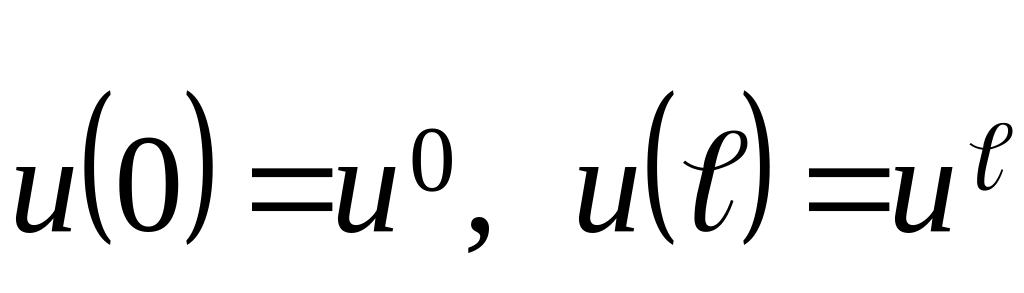предполагая, что

Определение:

Классическим решением задачи Дирихле будем называть функцию , удовлетворяющую первому уравнению и краевым (граничным условиям).

Краевые задачи для однородного уравнения с однородными граничными условиями будем называть ОДНОРОДНЫМИ краевыми задачами. Однородная краевая задача, например:

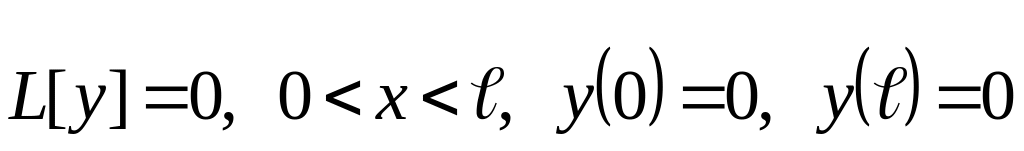
всегда имеет тождественно равное нулю, так называемое ТРИВИАЛЬНОЕ РЕШЕНИЕ . Может оказаться, что других решений задача не имеет. Это означает, что, решая на отрезке начальную задачу для уравнения

с начальными условиями (в силу теоремы 1 существования решения начальной задачи – такое решение существует и при не равно тождественно нулю), мы при всевозможных значениях получим функцию , обладающую тем же свойством, что и . (*)

Теорема 1:

Если , непрерывны на , то решение задачи (1) существует и единственно.

(*) Аналогичное положение будет и при задании соответствующих начальных условий на правом конце отрезка. Например, задача: , имеет только тривиальное решение

Больше не знаю, что сюда написать.