4. Сформулировать теорему Чаплыгина существования и единственности решения задачи Коши для уравнения первого порядка.
Задача Коши:
Особенность этой задачи в том, что она рассматривается на фиксированном промежутке времени.
Определение:
Функция
называется НИЖНИМ решением задачи Коши,
если выполнены неравенства:
Функция
называется ЫЕРХНИМ решением задачи
Коши, если выполнены неравенства:
Теорема:
Пусть существует нижнее
и верхнее
решение задачи Коши, такие что:
.
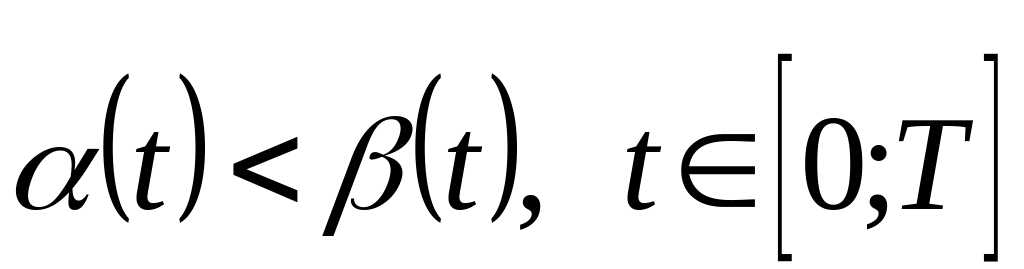Пусть функция
непрерывна и удовлетворяет условию
Липшица по переменной
:
Тогда задача Коши имеет единственное
решение
,
удовлетворяющее неравенствам:
Сформулировать теорему существования решения задачи Коши для уравнения первого порядка.
Условие 1: Пусть
задана в области
,
содержащей замкнутый прямоугольник
,
в которой
непрерывная и гладкая, следовательно,
существует
,
такая что:
,
при
.
Условие 2:
удовлетворяет в
условию Липшица (по переменной
):
,
где
- постоянная Липшица.
Теорема:
Пусть выполнены условия 1 и 2, тогда
существует единственное решение задачи
Коши на промежутке
,
где
.
Дайте определение фундаментальной системы решений линейного однородного дифференциального уравнения. Какой вид имеет общее решение этого уравнения? Пример.
Рассмотрим уравнение:
,
коэффициенты которого
непрерывны на интервале
.
Определение:
Будем говорить, что функции
ЛИНЕЙНО ЗАВИСИМЫ на интервале
,
если существуют постоянные
,
не все равные нулю, такие, что имеет
место тождество:
.
В противном случае (если они все равны
0) будем говорить, что
ЛИНЕЙНО НЕЗАВИСИМЫ.
Пусть
- решения первого уравнения.
Определение:
Назовём детерминант
ОПРЕДЕЛИТЕЛЕМ ВРОНСКОГО.
Теорема: Если решения
первого уравнения линейно зависимы на
,
то
на
.
Определение:
ФУНДАМЕНТАЛЬНОЙ СИСТЕМОЙ РЕШЕНИЙ
первого уравнения будем называть любые
линейно независимых решений этого
уравнения.
Пример:
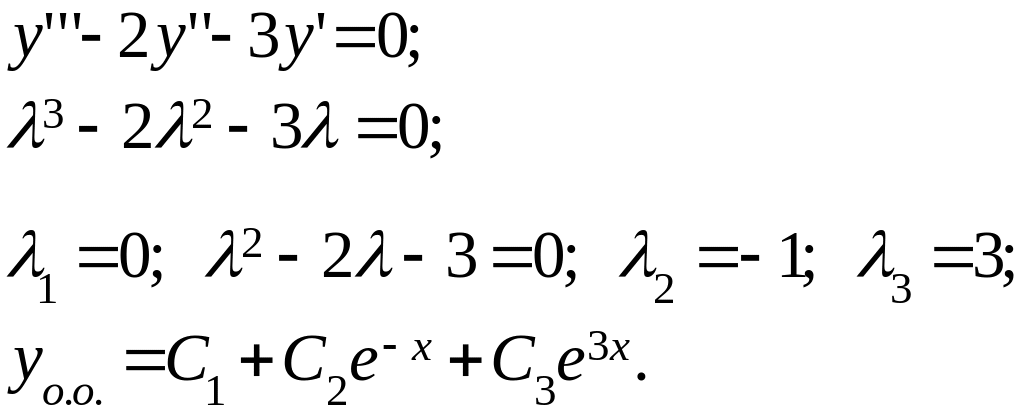
Метод вариации постоянной для решения неоднородного линейного оду первого порядка. Пример.
Уравнение называется ЛИНЕЙНЫМ, если оно линейно относительно неизвестной функции и её производных. Линейное уравнение первого порядка имеет вид:
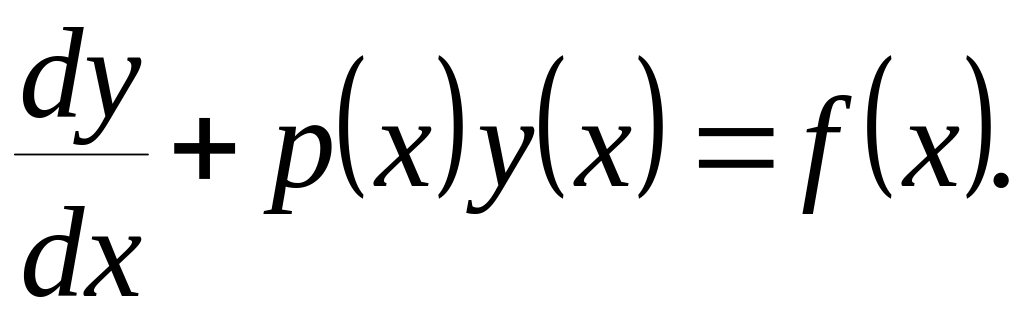
Если
,
то уравнение называется ОДНОРОДНЫМ:
,
Оно приводится к уравнению с разделяющимися
переменными
,
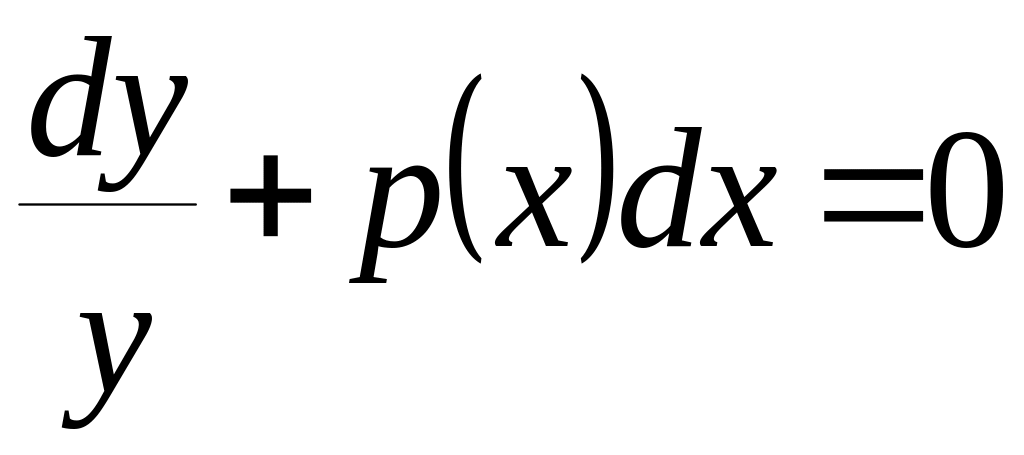общий интеграл которого имеет вид:
,
А общее решение:
Где
Решение первого линейного неоднородного
уравнения найдём методом вариации
постоянной, который состоит в том, что
мы используем специальную замену
неизвестной функции:
,
где
- функция, подлежащая определению (?!).
Подставляя такой вид решения в уравнение, получим:
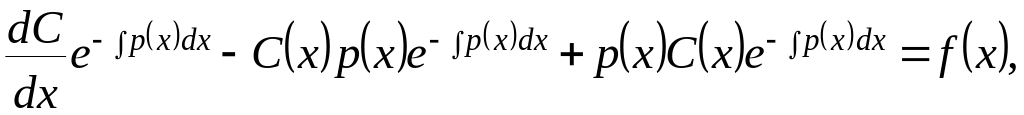откуда:
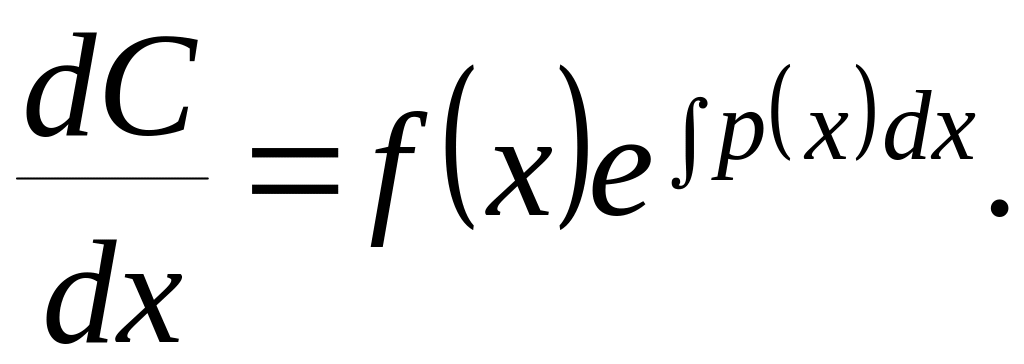
Интегрируя это равенство, найдём:
И окончательно:
Следовательно, общее решение линейного неоднородного уравнения представляется в виде суммы общего решения линейного однородного уравнения и частного решения неоднородного уравнения.
Пример:
Рассмотрим однородное уравнение:
которое соответствует данному
неоднородному уравнению. Это уравнение
с разделяющимися переменными. Его общее
решение имеет вид:
Общее решение неоднородного уравнения
ищем в виде:
Подставляя его в исходное уравнение,
получаем:
,
откуда
Итак:
