1) Физика – это наука о природе, св-вах и строении материи, о законах ее движения.

Основным методом исследования явл. опыт. Опыт – наблюдение исследуемых явлений в точно контролируемых условиях позволяющих следить за ходом явления и многократно воспроизводить их.

Гипотеза – научное предположение выдвигаемое для объяснения какого-либо явления и требующее проверки на опыте.

Теория – это успешно прошедшая проверку и доказанная гипотеза.

Величина Обозн.вел. Ед. изм. Обозн. ед.

длина L метр м

масса M килогр. кг

время T сек с

сила тока I ампер А

термод. темп. θ кельвин К

кол-во в-ва ν моль моль

сила света J кандела кд

2) Механическим движением называют измене­ние положения тела (или его частей) относительно других тел. Например, человек, едущий на эскалато­ре в метро. Тело, относительно которого рассматривается движение, его называют телом отсчета. Система ко­ординат, тело отсчета, с которым она связана, и вы­бранный способ измерения времени образуют си­стему отсчета. Направленный отрезок прямой, проведенный из начального положения движущейся точки в ее конечное положение, называется перемещением (s) Скорость — векторная физическая величина, характеризующая быстроту перемещения тела, чис­ленно равная отношению перемещения за малый промежуток времени к величине этого промежутка. Ускорение — векторная физическая величина, характеризующая быстроту изменения скорости, численно равная отношению изменения скорости к промежутку времени, в течение которого это измене­ние произошло. Характеристики механического движения свя­заны между собой основными кинематическими уравнениями.

s = v_0t + at²/ 2;

v = v₀ + at.

3) Предположим, что тело движется без уско­рения (самолет на маршруте), его скорость в течение продолжительного времени не меняется, а = 0, тогда кинематические уравнения будут иметь вид: v = const, s = vt.

Движение, при котором скорость тела не ме­няется, т. е. тело за любые равные промежутки вре­мени перемещается на одну и ту же величину, назы­вают равномерным прямолинейным движением.

Во время старта скорость ракеты быстро воз­растает, т. е. ускорение а > О, а == const.

В этом случае кинематические уравнения вы­глядят так: v = v₀ + at, s = V_0t + at²/ 2.

При таком движении скорость и ускорение имеют одинаковые направления, причем скорость изменяется одинаково за любые равные промежутки времени. Этот вид движения называют равноуско­ренным.

При торможении автомобиля скорость умень­шается одинаково за любые равные промежутки вре­мени, ускорение меньше нуля; так как скорость уменьшается, то уравнения принимают вид:v = v₀ + at, s = v_0t - at²/ 2.Такое движение называют равнозамедленным.

4) Криволинейные движения – движения, траектории которых представляют собой не прямые, а кривые линии.

Криволинейное движение – это всегда движение с ускорением, даже если по модулю скорость постоянна. Криволинейное движение с постоянным ускорением всегда происходит в той плоскости, в которой находятся векторы ускорения и начальные скорости точки. В случае криволинейного движения с постоянным ускорением в плоскости xOy проекции vxи vy ее скорости на оси Ox и Oy и координаты x и y точки в любой момент времени t определяется по формулам

Частным случаем криволинейного движения – является движение по окружности. Движение по окружности, даже равномерное, всегда есть движение ускоренное: модуль скорости все время направлен по касательной к траектории, постоянно меняет направление, поэтому движение по окружности всегда происходит с центростремительным ускорением где r – радиус окружности.

Вектор ускорения при движении по окружности направлен к центру окружности и перпендикулярно вектору скорости.

При криволинейном движении ускорение можно представить как сумму нормальной и тангенциальной составляющих 5)

5) Ускорение – характеризует быстроту изменения скорости.

Полное ускорение разделяют на 2 составляющих:

1) Тангенциальное ускорение (касательное) – характеризует изменение скорости по величине.

2)Нормальное – характеризует изменение скорости по направлению

6) Первый закон Ньютона: всякая материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока воздействие со стороны других тел не заставит ее изменить это состояние,он выполняется только в инерциальных системах отсчета.

ИНЕРЦИАЛЬНАЯ система отсчета-в которой справедлив закон инерции: материальная точка, на которую не действуют никакие силы, находится в состоянии покоя или равномерного прямолинейного движения.Любая система отсчета, движущаяся относительно инерциальной системы отсчета поступательно, равномерно и прямолинейно, также является инерциальной системой отсчета

7) Масса – это количественная мера инертности. Свойство тела оказывать сопротивление при попытках изменить модуль или направление его скорости называется инертностью. [m]=1кг m_c= ∑m_i

Импульсом тела называют векторную физи­ческую величину, являющуюся количественной ха­рактеристикой поступательного движения тел. Им­пульс обозначается р. Единица измерения импульса Р — кг • м/с. Импульс тела равен произведению мас­сы тела на его скорость: р = mv. Направление векто­ра импульса р совпадает с направлением вектора скорости тела v

8) 2-й закон Ньютона: Ускорение, которое приобретает тело прямо пропорционально результирующей всех сил, действующих на тело и обратно пропорционально массе.

,

Сила - количественная хар-ка интенсивности механического взаимодействия.

Сила – это векторная величина являющаяся мерой механического воздействия на тело со стороны других тел или полей в результате которого изменяется скорость тела или тело изменяет форму и размер.

Виды сил: 1) контактные, возникают при соприкосновении тел (сила трения, упругости); 2) дальнодействующие (полевые), возникают между телом и силовым полем.

9) Третий закон Ньютона:всякое действие материальных точек (тел) друг на друга носит характер взаимодействия; силы, с которыми действуют друг на друга материальные точки, всегда равны по модулю, противоположно направлены и действуют вдоль прямой, соединяющей эти точки:F₁₂=-F_2I,где F₁₂-сила, действующая на первую материальную точку со стороны второй; F₂₁-сила, действующая на вторую материальную точку со стороны первой. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

10).Понятие состояния в классической физике. Границы применимости классического способа описания движения частиц.Важным свойством замкнутых термодинамических систем является существование у них равновесных состояний, в которых они могут пребывать сколь угодно долго. Для газа, заключенного в некотором сосуде, равновесным является состояние, в котором температура, давление и плотность (или число молекул в единице объема) в пределах объема газа одинаковы. Если в каком-нибудь месте этого объема вызвать местное нагревание или сжатие, то в системе начнется процесс выравнивания температур и давления. Этот процесс будет происходить в течение того времени, пока имеется внешнее воздействие. Однако только после прекращения этого воздействия процесс выравнивания приведет систему к новому равновесному состоянию.

В термодинамике продолжало “работать” и понятие неравновесного состояния. Состояния изолированных термодинамических систем, в которых они, несмотря на отсутствие внешних воздействий, не могут пребывать в течение конечных промежутков времени, называются неравновесными. Система, первоначально находящаяся в неравновесном состоянии, с течением времени переходит в равновесное состояние.

Границы применения: А) применима лишь к сравнительно медленным движениям со скоростями, заметно меньшими скорости света в вакууме c≈ 300000 км/с Б) заключается в ее неприменимости к описанию явлений микромира, то есть к движениям тел малой массы в малых участках пространства.

11)Внутренние и внешние силы.

Система материальных точек - такая совокупность материальных точек, в которой движение каждой точки зависит от положений или движений всех остальных точек

В механике внешними силами по отношению к данной системе материальных точек называются те силы, к-рые представляют собою действие на эту систему других тел (других систем материальных точек), не включенных нами в состав данной системы. Внутренними силами являются силы взаимодействия между отдельными материальными точками данной системы. Подразделение сил на внешние и внутренние является совершенно условным: при изменении заданного состава системы некоторые силы, ранее бывшие внешними, могут стать внутренними, и обратно.

Скорость изменения импульса системы равна главному вектору всех внешних сил, действующих на эту систему.

12) Закон сохранения импульса: Если равнодействующая всех сил, приложенных к замкнутой системе материальных точек равна нулю, то суммарный импульс в замкнутой системе остается постоянным.

Условие применимости закона импульса:

1)

2)

13) Центр инерции – это геометрическая точка С, характеризующая движение тела или системы частиц как целого, координаты которо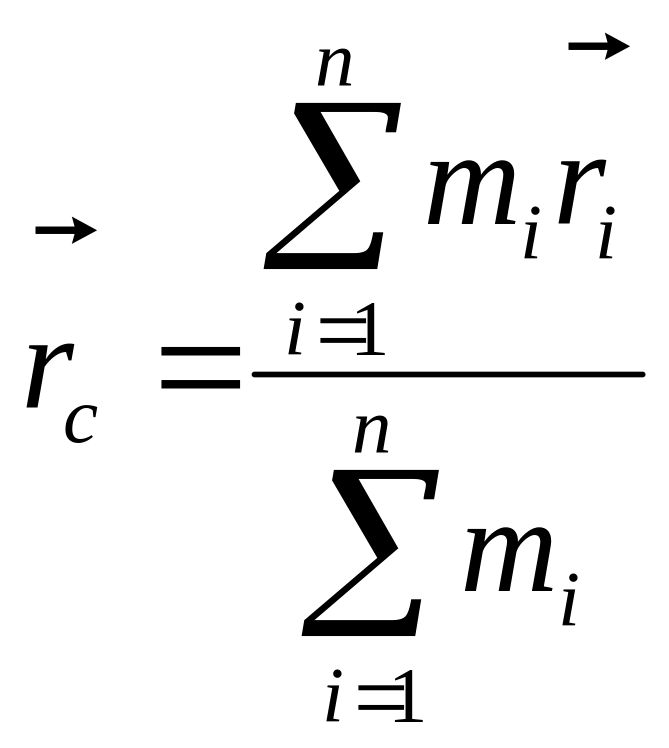й: где mi b ri – масса и радиус-вектор i-й материальной точки. 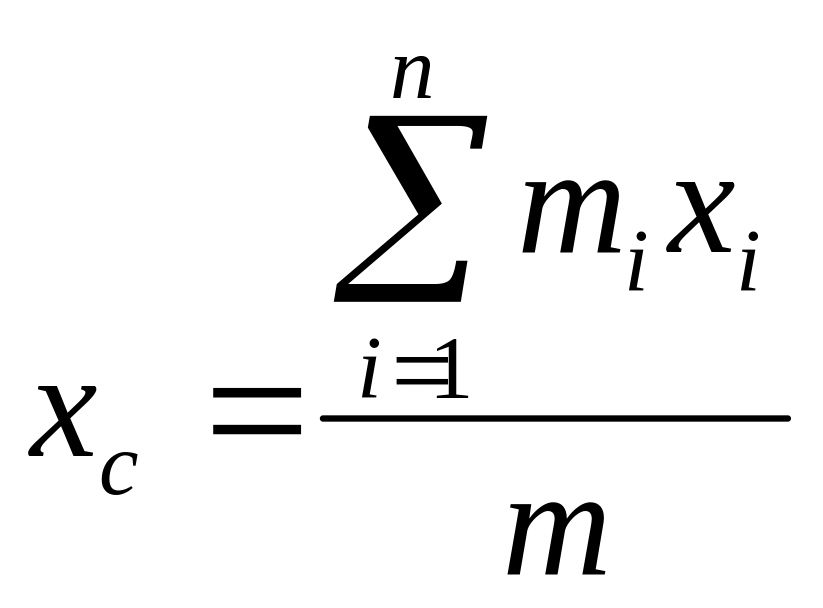аналогично y,z

Теорема о движении центра масс(инерции): центр масс системы материальных точек движется как материальная точка, масса которой равна суммарной массе всей системы, а действующая сила – геометрической сумме всех внешних сил, действующих на все точки системы.

14) Движение тел с переменной массой t:m,ṽ t+dt m+dm v+dv dm<0 (v и р - вектора)

d̃p=Fdt

d̃p = [(m+dm) (ṽ+dv)+v2m2]- mv

d̃p=mv+mdv+vdm+dmdv+v2dm2-mv= mdv+vdm+v2dm2

dm=–dm2

v_отн=v2–v (mdv)/dt=(dm/dt)v_отн+F ­­– ур-ние Мещерского

F_p= (dm/dt)v_отн – реактивная сила

(mdv)/dt= F_p+F

15) Работой A, совершаемой постоянной силой называется физическая величина, равная произведению модулей силы и перемещения, умноженному на косинус угла α между векторами силы F̃ и перемещения s̃: A=Fscosα dA=Fdr=Fdscosα= F_sds A=∫ F_sds

Работа силы, совершаемая в единицу времени, называется мощностью. Мощность P это физическая величина, равная отношению работы A к промежутку времени t, в течение которого совершена эта работа:

P=A/t [Вт=дж/с]

16) Кинетическая энергия (энергия механического движения) – происходит под действием силы F и равна работе, совершенной этой силой. Изменение кинетической энергии происходит за счет работы внешних сил.

dWk = dA = Fdr ; dr = vdt ; dWk = Fdr = F v dt = vdP

F = dP / dt = 1/m * vdP = d(P[ст.2] / 2m) ; dWk = d(P[ст.2] / 2m) ;

Wk = P[ст.2] / 2m = mv(ст.2) / 2

17) Консервативные и неконсервативные силы.

Консервативными силами наз силы работа которых не зависит от траектории движения тела, а зависит только от начального и конечного положения тела. Для консервативной силы работа по перемещению тела по замкнутой траектории равна нулю.

A = (интеграл с кружком в центре) Fdt=0 – условие потенциальной силы.

В противном случае сила называется диссепативной. Дессипативная сила зависит от скорости точек и совершает отрицательную работу.

N = dA / dt – мгновенная мощность

Неконсервативные силы – действующие силы при перемещении тела из одного положения в другое зависит от формы траектории движения.

Потенциальная энергия – это механическая энергия системы тел определяемая их взаимным положением и характером сил взаимодействия между ними.

18) Закон сохранения энергии – энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного типа в другой.

Все законы сохранения связаны с определенными свойствами симметрии пространства и времени. Закон сохранения импульса связан с однородностью пространства, т.е. вид физических знаков не изменяется при параллельном переносе в пространстве системы отсчета. Закон сохранения энергии связан с однородностью времени, т.е. выбор начала отсчета времени не изменяет физических законов или физические законы инвариантны относительно выбора начала отсчета времени.

19) Соударение тел. Существует 2 вида предельных ударов: абсолютно упругий и абсолютно неупругий.

Абсолютно упругим ударом называется столкновение тел, в результате которого их внутренние энергии не меняются. Рассмотрим центральный удар двух шаров, движущ-ся навстречу друг другу:

m1v1+m2v2=m1u1+m2u2 и (m1v1²)/2+(m2 v2²)/2=(m1u1²)/2+(m2 u2²)/2

u1=[(m1-m2)v1+2m2v2]/(m1 +m2) u2=[(m2-m1)v2+2m1v1]/(m1+m2)

Абсолютно неупругим ударом, называется столкновение двух тел, в результате которого они соединяются вместе и движутся дальше как одно тело. Рассмотрим абс. неупругий удар на примере столкновения двух шаров. Пусть они движутся вдоль прямой, соединяющей их центры, со скоростями v1 и v2 m1v1+m2v2=(m1+m2)V ? V=(m1v1+m2v2)/(m1+m2)

Кин. энергии системы до удара и после: K1=1/2(m1v1²+m2v2²) K2=1/2(m1+m2)V

20) Степени свободы — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Также число степеней свободы равно полному числу независимых уравнений, полностью описывающих динамику системы.

Простейшая механическая система — материальная точка в трёхмерном пространстве — обладает тремя степенями свободы, так как её состояние полностью описывается тремя пространственными координатами.

Абсолютно твёрдое тело обладает шестью степенями свободы, так как для полного описания положения такого тела достаточно задать три координаты центра масс и три угла, описывающих ориентацию.

Реальные тела обладают огромным числом степеней свободы (порядка числа частиц, из которых состоит тело). Однако в большинстве ситуаций оказывается, что наиболее важны лишь несколько «коллективных» степеней свободы, характеризующих движение центра масс тела, его вращение, его деформацию, его макроскопические колебания.

21) Моментом силы относительно неподвижной точки О называется векторная величина, равная векторному произведению радиус-вектора r, проведенного из точки О в точку приложения силы А, на вектор силы. М=Fr Модуль момента силы: М= Fr sin a=Fl

Где а – угол между векторами r и F, l – длина перпендикуляра опущенного из точки О на линию действия силы и называемого плечом силы. При переносе точки приложения силы вдоль линии ее действия, момент этой силы относительно одной и той же неподвижной точки О не изменяется. Если линия действия силы проходит через точку О, то момент силы относительно этой точки равен 0.

Моментом силы относительно неподвижной оси а называется скалярная величина , равная проекции на эту ось вектора М момента силы F Относительно произвольной точки О оси а. Значение момента Ма не зависит от выбора положения точки О на оси а. Если линия действия силы пересекает ось или параллельна ей, то момент силы относительно этой оси равен 0. Результирующий момент относительно неподвижной оси а равен алгебраической сумме моментов относительно этой оси всех сил системы.