2.2 Решение задачи.

Найти приближённо обратную матрицу для матрицы А с точностью до 0,001 по схеме единственного деления.

А= =

Для удобства поместим вычисления в таблицу .

а1	а2	а3	а4	j1	j2	j3	j4	∑по строке	∑контр
1,7	9,9	-20	-1,7	1	0	0	0	-9,1	-9,1
20	0,5	-30,1	-1,1	0	1	0	0	-9,7	-9,7
10	-20	30,2	0,5	0	0	1	0	21,7	21,7
3,3	-0,7	3,3	20	0	0	0	1	26,9	26,9
1	5,823529	-11,7647	-1	0,588235	0	0	0	-5,35294	-5,35294
0	115,9706	-205,194	-18,9	11,76471	-1	0	0	-97,3588	-97,3588
0	78,23529	-147,847	-10,5	5,882353	0	-1	0	-75,2294	-75,2294
0	19,91765	-42,1235	-23,3	1,941176	0	0	-1	-44,5647	-44,5647
	1	-1,76936	-0,16297	0,101446	-0,00862	0	0	-0,83951	-0,83951
	0	9,420391	-2,25019	2,054273	-0,67461	1	0	9,549861	-9,54986
	0	6,881973	20,05397	0,079381	-0,17175	0	1	27,84358	-27,8436
		1	-0,23886	0,218067	-0,07161	0,106153	0	1,013744	-1,01374
		0	-21,6978	1,421348	-0,32108	0,73054	-1	-20,867	-20,867
			4стр	-0,06551	0,014798	-0,03367	0,046088
			3стр	0,20242	-0,06808	0,09811	0,011009
			2стр	0,448924	-0,12666	0,168106	0,026989
			1стр	0,289816	-0,04848	0,141602	0,018428

3. Нахождение определителя матрицы

3.1 Теоретическая часть.

Пусть

A= 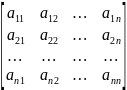(1)

и ∆=detA (2)

Рассмотрим линейную систему Ax=0 (3)

При решении системы (3) по методу Гаусса мы заменяли матрицу А треугольной матрицей В, состоящей из элементов отмеченных строк

B=

В результате получалась эквивалентная система Bx=0 (4)

Элементы матрицы В последовательно получались из элементов матрицы А и дальнейших вспомогательных матриц , ,… , , с помощью следующих элементарных преобразований:

1. Деления на «ведущие» элементы , , … , , которые предполагались отличными от нуля

2. Вычитания из строк матрицы А и промежуточных матриц ( i=1,2, … , n-1 ) чисел, пропорциональных элементам соответствующих ведущих строк. При первой операции определитель матрицы также делится на соответствующий «ведущий» элемент, при второй— определитель матрицы остается неизменным. Поэтому

det B = 1 =

Следовательно,

∆ = = (5)

т. е. определитель равен произведению «ведущих» элементов для соответствующей схемы Гаусса. Отсюда заключаем, что приведенная схема единственного деления , в предыдущем методе, может быть использована для вычисления определителей, причем столбец свободных членов тогда становится излишним.

Заметим, что если для какого-нибудь шага элемент или близок к нулю (что влечет за собой уменьшение точности вычислений), то следует соответствующим образом изменить порядок строк и столбцов матрицы.