Изгиб с кручением. Круглые валы.

Когда в поперечном сечении бруса равен нулю только один внутренний силовой фактор – продольная сила , такой вид деформации называют изгибом с кручением.

Изгибу с кручением подвергаются валы различных видов механических передач (ременные, зубчатые и т.д.).

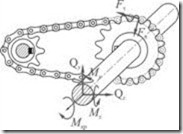
Рис. 2.7.1

Например, воздействие ролика звена цепи на зуб шестерни цепной передачи (рис.2.7.1.) будет способствовать возникновению в произвольном поперечном сечении вала пяти внутренних силовых факторов: , , , , . В данном случае можно сказать, что вал испытывает деформацию изгиба с кручением.

При изгибе с кручением в поперечном сечении возникают нормальные напряжения от изгиба в двух плоскостях, а так же касательные напряжения от кручения и изгиба.

Для расчета вала в первую очередь необходимо установить опасные сечения. Для этого строят эпюры изгибающих моментов и крутящего момента, предварительно разложив нагрузки на составляющие вдоль координатных осей (рис. 2.7.2)

Изгиб вала круглого и кольцевого поперечного сечения под действием изгибающих моментов и можно привести к прямому изгибу под действием результирующего (суммарного) изгибающего момента (рис. 2.7.3, а)

(2.7.1)

Вектор момента М в разных сечениях может иметь различные направления, в силу чего даже при отсутствии распределенных нагрузок эпюра М может быть криволинейной. Но при построении эпюры М обычно несколько завышают значения суммарного изгибающего момента, делая данные эпюры прямолинейными. Вычисляются значения суммарных моментов лишь для тех сечений, где на эпюрах и (или) есть переломы. Эти величины откладывают в масштабе по одну сторону от оси на эпюре М и соединяют прямой линией.

31

ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ - СЖАТИЕ   Внецентренным растяжением (сжатием) называется такой вид нагружения, при котором равнодействующая внешних сил не совпадает с осью стержня, как при обычном растяжении (сжатии), а смещена относительно продольной оси и остается ей параллельной. Оси X и Y - центральные (S_X = S_Y = 0) и главные (I_XY = 0)оси инерции поперечного сечения. Нормальные напряжения в поперечном сечении от действия силы Р смещенной относительно центра тяжести в точку А с координатами Х_P и Y_P (рис. 7.2, а.б) , определяются по формуле: Р - равнодействующая внешних или внутренних сил; F - площадь поперечного сечения; Х_P, Y_P - координаты точки приложения силы Р. х, у - текущие координаты точки, в которой определяется напряжение ; i_x, i_y - главные радиусы инерции поперечного сечения. 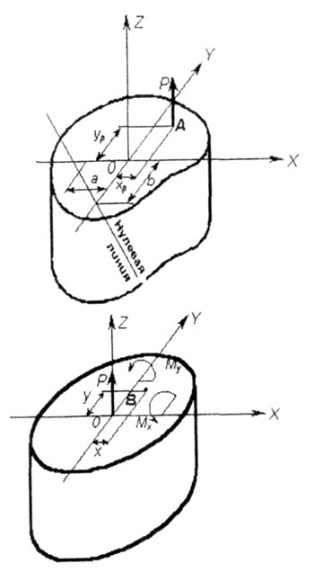Рис. 7.2 Квадраты главных радиусов инерции определяются по формулам: 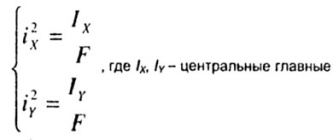моменты инерции поперечного сечения. Уравнение нулевой линии. Так как Р # 0, то из этого выражения следует Нулевая линия - прямая (Рис. 7.2, а). Точки пересечения нулевой линии с осями координат определяются выражениями: Центром давления называют точку пересечения равнодействующей внешних или внутренних сил с плоскостью поперечного сечения. (На рис. 7.2, а центр давления - точка А.) При проектировании сооружений и различного рода опор из бетона, кирпичной кладки, чугуна и других материалов, плохо работающих на растяжение, основное требование - отсутствие растягивающих напряжений. Решение задачи опирается на свойство ядра сечения. Ядром сечения называют часть плоскости поперечного сечения, расположенную в окрестности центра тяжести удовлетворяющую условию: если центр давления располагается внутри или на границе ядра сечения, то в любой точке поперечного сечения с текущими координатами (х, у) возникают напряжения одного знака. Чтобы в поперечном сечении возникали напряжения одного знака, нулевая линия должна располагаться либо вне поперечного сечения, либо быть касательной к поперечному сечению, что используется при определении границ ядра сечения.