
Лекция 7
Определение 1
Авет
Определение 2
Частной
производной функции z=f(x,y)
по переменной x
называется предел отношения частного
приращения функции по переменной x
к приращению
 когда последнее стремится к 0:
когда последнее стремится к 0:
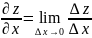
Замечание:
Особенность в обозначении частной
производной –
 вместо прямого d.
Аналогично определяется, и обозначаются
частная производная функции z=f(x,y)
по переменной y.
Для обозначения частных производных
функции z=f(x,y)
могут быть использованы другие символы:
вместо прямого d.
Аналогично определяется, и обозначаются
частная производная функции z=f(x,y)
по переменной y.
Для обозначения частных производных
функции z=f(x,y)
могут быть использованы другие символы:
 ,
,
Замечание: всё выше изложенное распространяется аналогично на случай функций 3-х и большего числа переменных
Определение 3
Полным дифференциалом функции z=f(x,y) называется сумма произведений частных производных этой функции на приращение независимых переменных т.е.
dz=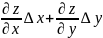
Замечание:
Дифференциалы независимых переменных
совпадают с их приращениями: dx=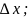 dy=
dy= поэтому дифференциал функции z=f(x,y)
вычисляется по формуле
поэтому дифференциал функции z=f(x,y)
вычисляется по формуле
dz= -основная
формула для полного дифференциала
функции 2-х переменных
-основная
формула для полного дифференциала
функции 2-х переменных
Определение 4
Авет
Теорема 1 (достаточное условие дифференцируемости функции 2-х переменных)
Если функция z=f(x,y) имеет частные производные в некоторой окрестности (x,y) причём эти частные производные непрерывны в самой точке (x,y) , то функция z=f(x,y) дифференцируема в этой точке
Определение 5
Выражения вида
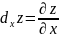 dx;
dx;
 dy
называются частными дифференциалами
функции z=f(x,y)
по переменной x
и y
соответственно
dy
называются частными дифференциалами
функции z=f(x,y)
по переменной x
и y
соответственно
Теорема 2
Если
z=f(x,y),
где x=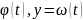 и каждая из функций дифференцируема,
то производная сложной функции z=f
и каждая из функций дифференцируема,
то производная сложной функции z=f может быть вычислена по формуле
может быть вычислена по формуле

Теорема 3
Если
z=f(x,y),
где x=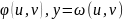 и каждая из функций дифференцируема,
то
и каждая из функций дифференцируема,
то
 =
=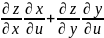 ;
;
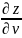 =
=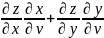
Определение 6
Частными производными 2-ого порядка от функции z=f(x,y) называется, частные производные от её частных производных первого порядка и обозначаются:
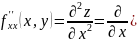 )
)
 )
)
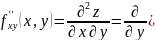 )
– дифференцирование сначала по x,
а затем по y
от полученного результата
)
– дифференцирование сначала по x,
а затем по y
от полученного результата
 )
)
Замечание: Частные производные 3-го и более высокого порядков от функции z=f(x,y) определяются и обозначаются аналогично
 )
)
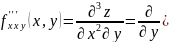 )
и т.д.
)
и т.д.
Определение 7
Частная производная высшего порядка взятая по различным переменным называется смешанной частной производной
Теорема 4
Смешанные производные, отличающиеся только порядком дифференцирования равны между собой, если они непрерывны
Лекция 8
Определение 1
Точка
 называется точкой MAX
(MIN)
функции z=f(x,y),
если существует окрестность
такая что для всех точек (x,y)
из этой окрестности выполняется
неравенство
называется точкой MAX
(MIN)
функции z=f(x,y),
если существует окрестность
такая что для всех точек (x,y)
из этой окрестности выполняется
неравенство
 (
(
Определение 2
MAX или MIN функции z=f(x,y) называется её экстремумом от точки в которой функция имеет экстремум называются точками экстремума
Замечание: Аналогично определяется экстремум функции 3-х и большего числа переменных
Определение 3
Точки, в которых, все частные производные первого порядка функции нескольких переменных равны 0 называются стационарными
Определение 4
Точки, в которых все частные производные первого порядка функции нескольких переменных равны 0 или не существует хотя бы одна из них называются критическими
Замечание: В критических точках каждая частная производная функции нескольких переменных равна 0 или не существует
Теорема 1(необходимое условие экстремума)
Если функция нескольких переменных достигает экстремума в какой-либо точке, то эта точка является критической.
Замечание: Обратное утверждение не всегда верно, т.е. не во всякой критической точке функции нескольких переменных имеет экстремум
Теорема 2 (достаточное условие экстремума)
Пусть функция z=f(x,y) имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки
Обозначим:
A=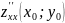 ;
B=
;
B=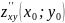 ;
C=
;
C=

Тогда:
1)Если
 то функция имеет экстремум в точке
а именно
то функция имеет экстремум в точке
а именно
MAX, если A<0
MIN, если A>0
2)Если
 ,
то функция не имеет экстремум в точке
,
то функция не имеет экстремум в точке
3)Если
 ,
то требуются дополнительное исследование
(сомнительный случай)
,
то требуются дополнительное исследование
(сомнительный случай)
Определение 5
Условным
экстремумом функции z=f(x,y)
называется экстремум этой функции,
достигнутый при условии, что переменные
x
и y
связаны между собой, так называемым
уравнением связи
 .
Отыскание условного экстремума функции
z=f(x,y)
при условии
,
можно свести к исследованию на обычный
экстремум вспомогательной функции –
так называемой функции Лагранжа, где
.
Отыскание условного экстремума функции
z=f(x,y)
при условии
,
можно свести к исследованию на обычный
экстремум вспомогательной функции –
так называемой функции Лагранжа, где
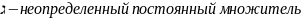 (множитель Лагранжа)
(множитель Лагранжа)
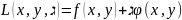
Теорема 3 (необходимое условие условного экстремума)
Точки экстремума z=f(x,y) при условии удовлетворяют системе из 3-х уравнений

