Лекция 4

Определение 1

Ряд вида называется степенным рядом. a₁, a₂,a₃, …,a_n… называется коэффициентами ряда.

Замечание!

Степенным рядом называется также ряд

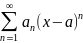, где а это некоторое постоянное число . Ряд данного вида, т.е. ряд сводится к ряду вида путем замены пееменной по формуле

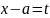
Замечание!

Придавая переменной х различные числовые значения будем получать различные числовые ряды, которые могут оказаться сходящимися или расходится.

Определение 2

Множества значений переменной х, при которых степенной ряд сходится, называется областью сходимости степенного ряда.

Теорема Абеля

Если степенной ряд 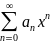сходится при некотором значении 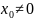, то он сходится и при том абсолютно, при всяком значении х удовлетворяем неравенству

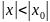
Следствие из теоремы Абеля

Существует такое число R, такое что при 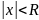ряд сходится, а при

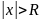- расходится. При этом число R называют радиусом сходимости, а 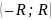интервалом сходимости степенного ряда

Замечание

На концах интервала сходимости x=R, x=-R ряд может как сходится, так и расходится.

Нахождение радиуса сходимости

1. Если среди коэфицентов ряда a₁, a₂,a₃, …,a_n…нет равных 0 т.е. ряд содержит все целые положительные степени х, то радиус сходимости можно найти по формуле

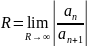при условии что этот предел существует и конечен( или бесконечен).

2. Если среды коэффициентов ряда есть равные 0, то интервал сходимости можно находить применяя непосредственно признак Даламбера или признак Коши к ряду, составленному из абсолютных величин членов исходного ряда.

Замечание!

Формула выражает радиус сходимости также и ряда

, а интервалом сходимости этого ряда

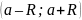
Замечание!

Если R=0, то ряд сходится лишь при х=0. Если же R=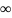

сходится на всей числовой прямой.

Свойства степенных рядов

1. Степенной ряд можно почленно интегрировать по

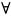
отрезку 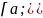принадлежащему его интервалу сходимости

2. Степенной ряд можно почленно дифференцировать любое число раз в интервале его сходимости.

Лекция 5

Определение 1

Ряд в правой части равенства называется рядом Тейлора для функции f(x)

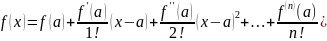
Замечание!

В сокращенной форме записи ряд Тейлора для функции f(x) имеет вид:

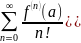, при этом по определению полагают 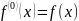,то есть производная нулевого порядка функции равна самой функции.

Определение 2

В частном случае, когда а=0 из ряда Тейлора получается ряд Маклорена

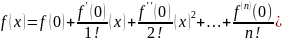
Замечание!

Сокращенная форма записи ряда Маклорена для функции f(x) имеет вид:

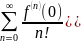
Теорема (достаточное условие представления функции её рядом Тейлора)

Если в интервале производные функции f(x) всех порядков ограничены одним и тем же числом С, С 0, то есть :

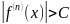, (n=1,2,3,…) то ряд Тейлора, для этой функции сходится в интервале и его сумма равна f(x)

Лекция 6

Определение 1

Пусть имеется n-переменных величин и каждому набору их значений (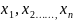 ) из некоторого множества Х соответствует одно вполне определенное значение переменной величины z, тогда говорят, что задана функция нескольких переменных

Замечание: Переменные ( ) при этом называются независимыми переменными или аргументами

z-зависимой переменной; f-означает закон соответствия, а множество X называется областью определения функции и обозначается D(z)

Замечание: Геометрически область определения функции двух независимых переменных представляет собой конечную или бесконечную часть плоскости, ограниченной одной или несколькими кривыми (границы области), которые могут принадлежать или не принадлежать данной области.

Определение 2

Совокупность всех значений функции z=f(x,y) – называется множеством её значений и обозначается символом E(z)

Определение 3

Графиком функции z=f(x,y) называется множество точек (x,y,z) в пространстве координаты которых удовлетворяют условиям z=f(x,y); (x,y)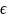 D(z)

Замечание: В простейших случаях такой график представляет собой некоторую поверхность

Замечание: Функция 3-х и большего числа переменных не имеют наглядного геометрического представления

Определение 4

Линией уровня функции z=f(x,y) называется множество точек на плоскости в которых функция принимает одно и то же значение С. Число С в этом случае называется уровнем.

Замечание: Построение линий уровня оказывается существенно более лёгкой задачей, чем построение графиков самих функций

Определение 5

Окрестностью точки на плоскости называется любой круг с центром данной точки за исключением его границы (открытый круг)

Определение 6

Число А называется пределом функции z=f(x,y) при x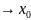 и y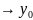 , если для любого числа 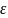>0 существует число 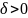такое что выполняется неравенство 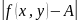< , при 0< < 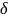, при это пишут: 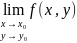=A

Замечание: Величина 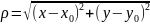, есть расстояние между точками (x,y) и (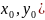 на плоскости

Определение 7

Функция z=f(x,y) называется непрерывной в точке ( :

• Если она определена в этой точке;

• Если она имеет конечный предел в этой точке;

• Если этот предел равен значению функции в этой точке т.е.

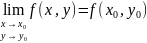
Замечание: Геометрический смысл непрерывности состоит в том, что график функции в некоторой окрестности ( представляет собой сплошную не расслаивающуюся поверхность

Определение 8

Если в точке ( не выполняется хотя бы одно из 3-х условий непрерывности z=f(x,y), то такая точка называется точкой разрыва функции z=f(x,y)

Замечание: Точки разрыва z=f(x,y) могут образовывать линии разрыва