57. A,b,z, y,g,h - формы записи уравнений.

“A” – форма записи уравнения четырехполюсника:

“В” – форма записи уравнения четырехполюсника:

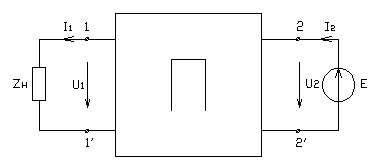
Найдём коэффициенты:

.

“Z” – форма записи уравнения четырехполюсника:

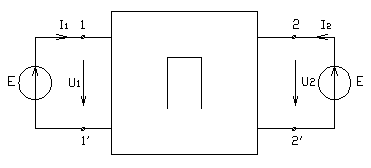
Найдём коэффициенты:

“Y” – форма записи уравнения четырехполюсника:

Найдём коэффициенты:

“H” – форма записи уравнения четырехполюсника:

.

“G” – форма записи уравнения четырехполюсника:

.

58. Т - образная схема замещения четырёхполюсника.“T ” – образная схема замещения (схема соединения - звезда).

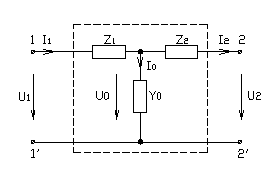
59. П - образная схема замещения четырёхполюсника.

(схема соединения - треугольник)

;

;

;

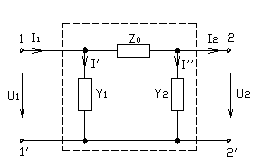
60. Определение коэффициента четырёхполюсника.

Коэффициенты четырехполюсника могут быть определены следующими способами: 1) Составляются уравнения по законам Кирхгофа, в которых первичные параметры U₁ и I₁ выражаются через вторичные U₂ и I₂. Полученные уравнения сравниваются основными уравнениями четырёхполюсника. 2) Схема четырехполюсника преобразуется к “Т”или “П”образной схеме замещения и затем по фора-м соответствия находим коэффициенты четырехполюсника. 3) Определяем входные сопротивления четырехполюсника для режимов холостого хода и короткого замыкания со стороны первичных и вторичных зажимов (основной способ).

3-ий способ нахождения коэффициентов четырёхполюсника:

- входное сопротивление схемы со стороны первичных зажимов при холостом ходе вторичных (зажимы 2 и 2’ - разомкнуты).

- входное сопротивление четырехполюсника со стороны первичных зажимов при коротком замыкании вторичных. (зажимы 2 и 2’ – замкнуты).

- входное сопротивление четырёхполюсника со стороны вторичных зажимов при холостом ходе первичных (зажимы 1 и 1’ – разомкнуты).

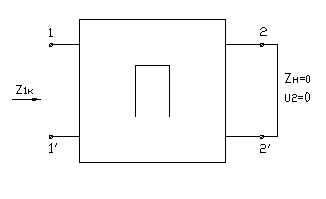
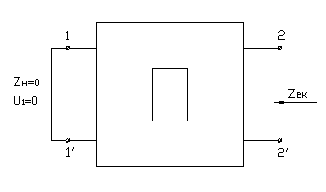
- входное сопротивление четырехполюсника со стороны вторичных зажимов при коротком замыкании первичных (зажимы 1 и 1’ - закорочены ).

Совмесное решение уравнений (1)-(4) не позволяет найти коэффициенты, но позволяют найти соотношение между , , , :

Для нахождения коэффициентов основных уравнений четырёёхполючника необходимо дополнить уравнения (1)-(4) уравнением связи между коэффициентами:

; ;

; .

Коэффициент A можно выразить следующим образом:

61. Характеристическое сопротивление четырехполюсника. В электросвязи широко используется режим работы симметричного четырехполюсника, при котором его входное сопротивление равно нагрузочному, т.е.

Это сопротивление обозначают как и называют характеристическим сопротивлением симметричного четырехполюсника, а режим работы четырехполюсника, для которого справедливо

называется режимом согласованной нагрузки.

В указанном режиме для симметричного четырехполюсника можно записать ;

62. Постоянная передачи четырехполюсника. Постоянная передачи четырехполюсника (мера передачи) _ – третий характеристический параметр. Для каждого четырехполюсника эта постоянная единственна. Рассмотрим физический смысл постоянной _. Для

симметричного четырехполюсника имеем

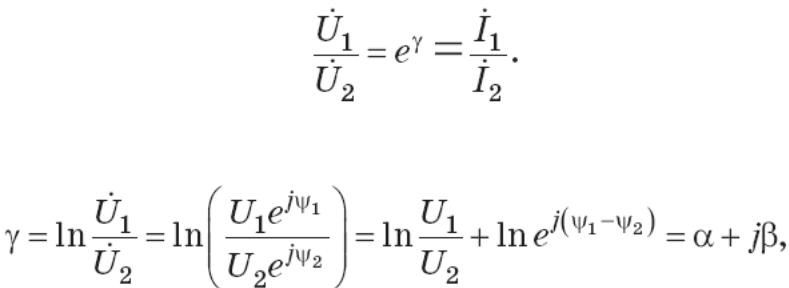
63.Уравнение четырехполюсника в гиперболических функциях. Запишем уравнение симметричного четырехполюсника с использованием коэффициента распространения. По определению .

 

Тогда

Решая (17) и (18) относительно  и , получим

  и 

Учитывая, что

и  , получаем уравнения четырехполюсника, записанные через гиперболические функции:

64.Сложные четырехполюсники.