
Финансовый университет при правительстве Российской Федерации
«Международный экономический факультет»,
специальность «Экономика (бакалавриат)»
Вопросы экзамена по математическому анализу за II семестр 1 года обучения
Раздел 1. «Интегральное исчисление»
Определение и теоремы о существовании и общем виде первообразной.
Пусть ф-ия y=f(x) задана на числовом промежутке. Тогда ф-ия y=F(x) называется первообразной для ф-ии y=f(x), если для любого x ͼ X выполняется F′(x) = f(x)
Теорема 1. Если ф-ия непрерывна на числовой прямой X ϵ R, то на этом промежутке у нее всегда есть первообразная
Теорема 2. Если для ф-ии на X ϵ R ф-ия Y=F(x) – первообразная, то ф-ия G(x) = F(x) + C дает общий вид первообразной
Четыре простейших свойства неопределенного интеграла.
[òf(x)dx]’ = (F(x)+C)’ = f(x)
d[òf(x)dx] = f(x)dx
òA×f(x)dx = A×òf(x)dx
ò[f(x)+g(x)]dx = òf(x)dx + òg(x)dx
Формула интегрирования по частям для неопределенного интеграла.
Пусть имеются дифференцируемые ф-ии u(x) и v(x) справедлива ф-ла:
(u(x)*v(x))′ = u′(x)*v(x)+u(x)*v′(x)
Тогда: ∫ (u′(x)*v(x)+u(x)*v′(x))dx = u(x)*v(x), отсюда ∫ (u′(x)*v(x))dx+∫(u(x)*v′(x))dx = u(x)*v(x) или ∫du*v + ∫u*dv = u*v
òu dv = uv – òv du
Правила
интегрирования выражений вида
![]() .
.
Применяется метод введения новой переменной:
а)
если
![]() ,
x
= a
sin
t
,
x
= a
sin
t
б)
если
![]() ,
x
= a
tg
t
,
x
= a
tg
t
в)
если
![]() ,
x
= a
/ cos
t
,
x
= a
/ cos
t
Затем использовать тождество sin2t + cos2t = 1
Интегрирование рациональных выражений с использованием «метода неопределенных коэффициентов».
Пример:
![]() разложим дробь в сумму элементарных:
разложим дробь в сумму элементарных:
![]()
![]()
![]()
Метод интегрирования путем замены переменной.
Теорема: Пусть для всех x ϵ X имеет место ∫f(x)dx = F(x) + C
Если x=g(t), для t ϵ T ϵ R и ф-ия g(t) имеет g’(t), тогда ∫f(x)dx = ∫f(g(x))dt = F(g(t)) + C
F(x) = F(g(t))
Подводим
функцию
![]() под
знак дифференциала:
под
знак дифференциала:
![]()
Раскрывая
дифференциал, легко проверить, что:

Фактически
![]() и
и
![]()
Методы интегрирования тригонометрических функций на примерах интегралов от четной и нечетной степеней синуса и косинуса, от степеней тангенса и котангенса.
Определенный интеграл, формула Ньютона-Лейбница.
Пусть
y=f(x)
непрерывная функция на отрезке [a,b]
и F(x)
одна из ее первообразных, т.е ![]() . Определенным интегралом от функции
y=f(x)
по отрезку [a,b]
называется число, которое обозначатся
в виде
. Определенным интегралом от функции
y=f(x)
по отрезку [a,b]
называется число, которое обозначатся
в виде ![]() при этом числа a
и b
называются пределами интегрирования
(нижним и верхним). Имеет место формула
Ньютона-Лейбница
при этом числа a
и b
называются пределами интегрирования
(нижним и верхним). Имеет место формула
Ньютона-Лейбница
![]()
Свойства определенного интеграла; интегрирование неравенств, теорема о «среднем значении функции».



Пусть а<c<b тогда


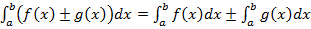
Если на [a,b] задана непрерывная функция f(x)≥0 то
 ≥0
≥0Если на [a,b] выполняется неравенство f(x)≤g(x) то

Для
непрерывной на отрезке [a,b]
функции f(x)
найдется такая точка C
что ![]() значение функции y=f(x)
определяемое
значение функции y=f(x)
определяемое ![]() называется средним значением функции
на отрезке.
называется средним значением функции
на отрезке.
Вычисление площади плоской фигуры с помощью определенного интеграла.
Пусть
на отрезке [a,b]
задана непрерывная функция y=f(x)≥0.
Найдем площадь фигуры ограниченной
сверху этой кривой y=f(x),
осью абсцисс и прямыми x=a
и х=b
. Если функция y=f(x)
непрерывная на отрезке [a,b]
то ![]()
Если
фигура располагается ниже оси Oх,
то y=f(x)≤0
для a≤x≤b
и ![]()
Определение интеграла от функции с бесконечным разрывом.
Пусть функция y=f(x) для a≤x≤b непрерывна, а в точке х=b имеет разрыв второго рода (бесконечный) в этом случае полагают
![]()
Если предел конечен, то говорят, что интеграл сходится; если предел бесконечен, то - расходится.
Замена переменной в определенном интеграле.
Пусть дан , где f(x) непрерывна на [a,b] введем новую переменную x=g(t)
Если:
g(α)=a ; g(β)=b, то [α,β] новый отрезок интегрирования;
g(t) и g’(t) непрерывны на [α,β];
f(g(t)) непрерывна на[α,β] тогда
![]()
Вычисление объема тела вращения с помощью определенного интеграла.
Объем тела вращения криволинейной трапеции abcd, где дуга ab - график непрерывной функции y=f(x) для x принадлежащего [a,b] находится по формуле
![]()
Если
кривая y=f(x)
вращающаяся вокруг оси Oу,
то надо найти обратную функцию x=g(y)
и для y=f(x)
применить формулу ![]()
Определение и теорема о вычислении двойного интеграла.
Если существует конечный предел Ѵ для функции z=f(x,y), то функция называется интегрируемой на множестве D. Cамо значение предела называется двойным интегралом функции z=f(x,y) на множестве D и обозначается

Если функция z=f(x,y) непрерывна на D и z=f(x,y)≥0 для всех (x,y)єD, то двойной интеграл численно равен объему Ѵ вертикального цилиндра, построенного на множестве D, как на основании и ограниченного сверху графиком функции z=f(x,y).
* Использование понятия определенного интеграла в экономике.
