17. Проверка гипотез о дисперсии. Распределение Фишера.

Проверка гипотезы о равенстве дисперсий двух выборок (критерий Фишера)

Генеральные совокупности Х и У распределены по нормальным законам N( , ) и N , ). Мат. ожид. неизвестно. , - выборочные дисперсии. Пусть > . Требуется при заданном уровне значимости проверить нулевую гипотезу : = . В качестве критерия проверки нулевой гипотезы примем случ. величину F= , которое имеет распределение Фишера с 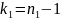, степенями свободы (при условии справедливости).

Вида альтернативных гипотез:

1. : > строят правостороннюю критическую область, где -квантиль распределения Фишера

Если F< - нулевая гипотеза принимается с уровнем значимости α.

2. : ≠ строят двустороннюю критическую область и сравнивают F= с табличным значением для двустороннего критерия Фишера .

Если F< - нулевая гипотеза принимается

Замечание

В случае если мат. ожид. известно, то в качестве проверки нулевой гипотезы : = рассматривают функцию критерия F= , которая имеет распределение Фишера с и степенями свободы.

Проверка гипотезы о равенстве дисперсий заданному числу

–выборки из ген.совокупности, распределенной по нормальному закону Х~N(α,σ).

Значение дисперсий неизвестно. -выборочная дисперсия.

Требуется при заданном уровне значимости α проверить гипотезу : =

Пусть мат. ожид. неизвестно. В качестве критерия проверки гипотезы примем случ. величина

Z= , которое имеет распределение с k=n-1 степенями свободы.

Вида альтернативных гипотез:

1. : > строят правостороннюю критическую область. Если Z< 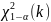нулевая гипотеза принимается с уровнем значимости α.

2. : < строят левостороннюю критическую область. Если Z> нулевая гипотеза принимается с уровнем значимости α.

3. : ≠ строят двустороннюю критическую область. Если <Z< => нулевая гипотеза принимается с уровнем значимости α.

Замечание

Если мат. ожид. известно, то в качестве критерия проверки нулевой гипотезы примем случ. величину Z= , где -- оценка дисперсии

18. Задача регрессии. Отыскание оценок параметров регрессии методом наименьших квадратов в случае линейной зависимости от параметров.

Регрессия — зависимость математического ожидания (например, среднего значения) случайной величины от одной или нескольких других случайных величин (свободных переменных), то есть  . Регрессионным анализом называется поиск такой функции  , которая описывает эту зависимость. Регрессия может быть представлена в виде суммы неслучайной и случайной составляющих. где   — функция регрессионной зависимости, а   — аддитивная случайная величина с нулевым мат. ожиданием. Линейная регрессия предполагает, что функция   зависит от параметров   линейно. При этом линейная зависимость от свободной переменной   необязательна, Метод наименьших квадратов — метод нахождения оптимальных параметров линейной регрессии, таких, что сумма квадратов ошибок (регрессионных остатков) минимальна. Метод заключается в минимизации евклидова расстояния   между двумя векторами — вектором восстановленных значений зависимой переменной и вектором фактических значений зависимой переменной.Постановка задачи. Задача метода наименьших квадратов состоит в выборе вектора  , минимизирующего ошибку  . Эта ошибка есть расстояние от вектора   до вектора  . Вектор   лежит в простанстве столбцов матрицы  , так как   есть линейная комбинация столбцов этой матрицы с коэффициентами  . Отыскание решения  по методу наименьших квадратов эквивалентно задаче отыскания такой точки  , которая лежит ближе всего к   и находится при этом в пространстве столбцов матрицы  . Таким образом, вектор   должен быть проекцией   на пространство столбцов и вектор невязки   должен быть ортогонален этому пространству. Ортогональность состоит в том, что каждый вектор в пространстве столбцов есть линейная комбинация столбцов с некоторыми коэффициентами  , то есть это вектор  . Для всех   в пространстве  , эти векторы должны быть перпендикулярны невязке  :

Так как это равенство должно быть справедливо для произвольного вектора  , то

Решение по методу наименьших квадратов несовместной системы  , состоящей из   уравнений с   неизвестными, есть уравнение

которое называется нормальным уравнением. Если столбцы матрицы   линейно независимы, то матрица   обратима и единственное решение

Проекция вектора   на пространство столбцов матрицы имеет вид

Матрица   называется матрицей проектирования вектора   на пространство столбцов матрицы  . Эта матрица имеет два основных свойства: она идемпотентна,  , и симметрична,  . Обратное также верно: матрица, обладающая этими двумя свойствами есть матрица проектирования на свое пространство столбцов. Пример построения линейной регрессии. Задана выборка — таблица

Задана регрессионная модель — квадратичный полином

Назначенная модель является линейной. Для нахождения оптимального значения вектора параметров   выполняется следующая подстановка:

      

Тогда матрица   значений подстановок свободной переменной   будет иметь вид

Задан критерий качества модели: функция ошибки

Здесь вектор  . Требуется найти такие параметры  , которые бы доставляли минимум этому функционалу,

Требуется найти такие параметры  , которые доставляют минимум   — норме вектора невязок  .

Для того, чтобы найти минимум функции невязки, требуется приравнять ее производные к нулю. Производные данной функции по   составляют

Это выражение также называется нормальным уравнением. Решение этой задачи должно удовлетворять системе линейных уравнений

то есть,

После получения весов можно построить график найденной функции.

19. Оценка параметров регрессии при разложении по ортогональному базису, свойства оценок.

20.Дисперсия адекватности. Проверка адекватности модели регрессии

21. Определение функций регрессии в корреляционном анализе

Определение функции регрессии. Вторая задача сводится к выяснению действия на зависимую переменную главных факторов или причин, при неизменных прочих равных условиях, и при условии исключения воздействия на зависимую переменную случайных элементов. Функция регрессии определяется в виде математического уравнения того или иного типа.

22. Линейная корреляция. Коэффициент корреляции, его свойства и назначение.

Ковариация – это число, равное мат. ожиданию произведения отклонений случайных величин от своих мат. ожиданий

Cov(X,Y)=M((X-M(X))*(Y-M(Y)))

Для дискретных случайных величин

Свойства ковариации:

1. Cov(X,Y)= Cov(Y,X)

2. Cov(X,Y)=M(X*Y) - M(X)*M(Y) => M(X,Y) = M(X)*M(Y) + Cov(X,Y)

Доказательство:

Cov(X,Y) = M((X-M(X))*(Y-M(Y))) = M[X*Y-M(X)*Y-M(Y)*X+M(X)*M(Y)] = M(X*Y)-M(M(X)*Y)-M(M(Y)*X)+M(M(X)*M(Y)) = M(X*Y)-M(X)*M(Y)-M(Y)*M(X)+M(X)*M(Y) = M(X*Y)- M(X)*M(Y)

3. D(X+Y) = D(X)+D(Y)+2*Cov(X,Y)

Доказательство:

D(X+Y) = M[((X+Y) – M(X+Y))²] = M[(X+Y)² – 2*M(X+Y)*(X+Y)+M²(X+Y)] = M((X+Y)²)-M(2*M(X+Y)*(X+Y))+M(M²(X+Y))=M(X²)+2*M(X*Y)+M(Y²)-2*M(X+Y)*M(X+Y)+M²(X+Y) = M(X²)+2*M(X*Y)+M(Y²)-M²(X+Y)=M(X²)+2 *M(X*Y)+M(Y²)-M²(X)-2*M(X)*M(Y)-M²(Y)=M(X²)-M²(X)+M(Y²)-M²(Y)+ 2 *M(X*Y)-2*M(X)*M(Y)=D(X)+D(Y)+2*Cov(X,Y)

4. Если X и Y независимы, то Cov(X,Y)=0

Доказательство:

M(X*Y) = M(X)*M(Y) – по определению независ. сл. вел. => M(X*Y)-M(X)*M(Y)=0

Замечание:

Если Cov(X,Y)<>0, то случайные величины зависимы. Однако, из Cov(X,Y)=0 не следует независимость случайных величин.

5. |Cov(X,Y)|<=сигма(X)*сигма(Y),

причём равенство имеет место тогда и только тогда, когда случайные величины связаны строгой линейной зависимостью, то есть Y=альфа*X+бета

Доказательство:

1. k(x, y) = k(y, x)

2. k(x1 + x2, y) = k(x1, y) + k(x2, y), т.к.

k(x1 + x2, y) = M((x1 + x2) y) – M(x1 + x2)M(y) = M(x1y+x2y) – (M(x1)+M(x2))*M(y) = M(x1y) + M(x2y) – M(x1)M(y) – M(x2)M(y) = k(x1, y) + k(x2, y)

3. k(ax, y) = ak(x, y)

4. k(x, x) = D(x) >=0

k(x, x) = D(x) = 0  x = a = const

Скалярное произведение

k(x, y) – скалярное произведение в линейном пространстве случайных величин.

Неравенство Коши-Буняковского:

|(x, y)| <= ||x||*||y||, где ||x|| = sqrt((x, x)) => |k(x, y)| <= sqrt(k(x, x))*sqrt(k(y, y)) = сигма(x)*сигма(y)

Y = ax + b => k(x, y) = k(x, ax + b) = k(x, ax) + k(x, b) = ak(x, x) = ak(x, x) + 0 = aD(x) => |k(x, x)| = |a|*sqrt(k(x, x)*k(x, x))

Y = ax + b  p = +- 1

Определение: Случайные величины называются коррелированными, если их ковариация отлична от нуля. Если cov(X, Y) = 0, то случайные величины называются некоррелированными.

Определение: Коэффициентом корреляции случайной величины X и Y называется число

P(X, Y) = cov(X, Y)/(сигма(X)*сигма(Y))

1. P(X, Y) = P(Y, X)

2. |P(X, Y)| <= 1, причем P = +- 1 тогда и только тогда, когда случайные величины связаны строгой линейной зависимостью.

3. Если X и Y – независимы, то P(x, y) = 0

4. P^2(X, Y) не меняется при линейных преобразованиях случайных величин, то есть P^2(ax+b, gy + q) = P^2(x, y)

Ковариационная матрица случайного вектора X=(x1, x2, …, xn) называется матрица K(x)б элементами которой являются числа

Kij = cov(Xi, Xj) = M((Xi – M(Xi))^2) = D(Xi)

Определитель ковариационной матрицы называется обобщенной дисперсией.

Ее можно использовать как меру рассеяния n-мерной случайной величины.